Exemplos: Utilizando as Propriedades I e II, simplifique as raízes abaixo:
Exercícios Resolvidos
1) Dada a raiz abaixo, simplifique utilizando as propriedades I e II:
Rascunho:
Então:
2) Dada a raiz abaixo, simplifique utilizando as propriedades I e II:
Vamos reescrever separadamente a raiz complexa acima:
Agora podemos substituir os valores de a, b, c e d em B:
3) Dada a raiz abaixo, simplifique utilizando as propriedades I e II:
4) Dada a raiz abaixo, simplifique utilizando as propriedades I e II:
Faça o Download em PDF aqui.



![clip_image002[3] clip_image002[3]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q4LXjGRPI/AAAAAAAAEMQ/KGKqiDeRo6I/clip_image002%5B3%5D_thumb.gif?imgmax=800)
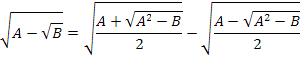
![clip_image006[4] clip_image006[4]](http://lh4.ggpht.com/_Qmjqb2Gk9no/S3q4T7gaCGI/AAAAAAAAENI/f5r_hsSB5Hc/clip_image006%5B4%5D_thumb.gif?imgmax=800)
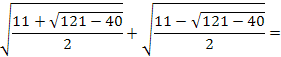
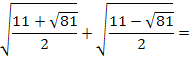
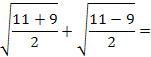
![clip_image006[6] clip_image006[6]](http://lh4.ggpht.com/_Qmjqb2Gk9no/S3q4cq5_H2I/AAAAAAAAEOA/E56UshItK64/clip_image006%5B6%5D_thumb.gif?imgmax=800)
![clip_image008[4] clip_image008[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q4d_s_caI/AAAAAAAAEOI/U7X2WCkpYJk/clip_image008%5B4%5D_thumb.gif?imgmax=800)
![clip_image010[4] clip_image010[4]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q4fXt-c4I/AAAAAAAAEOQ/CZ8RmC7ygH0/clip_image010%5B4%5D_thumb.gif?imgmax=800)
![clip_image012[4] clip_image012[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q4gQQpABI/AAAAAAAAEOY/mBF0-sVdgLw/clip_image012%5B4%5D_thumb.gif?imgmax=800)
![clip_image014[4] clip_image014[4]](http://lh3.ggpht.com/_Qmjqb2Gk9no/S3q4hhPav4I/AAAAAAAAEOg/IAitaSOZnEk/clip_image014%5B4%5D_thumb.gif?imgmax=800)
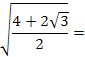
![clip_image002[15] clip_image002[15]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q5HYiWLNI/AAAAAAAAESQ/2NJo2Jloj20/clip_image002%5B15%5D_thumb.gif?imgmax=800)
![clip_image002[17] clip_image002[17]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5IZq9HqI/AAAAAAAAESY/aHBlR8yNrMY/clip_image002%5B17%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image002[21] clip_image002[21]](http://lh4.ggpht.com/_Qmjqb2Gk9no/S3q5Tfo0W2I/AAAAAAAAETg/JSTg6s5L9jU/clip_image002%5B21%5D_thumb.gif?imgmax=800)
![clip_image004[18] clip_image004[18]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5U0Tr_BI/AAAAAAAAETo/l6gEITBGQJ8/clip_image004%5B18%5D_thumb.gif?imgmax=800)
![clip_image006[14] clip_image006[14]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q5WQPygzI/AAAAAAAAETw/Qnp0H8vULqQ/clip_image006%5B14%5D_thumb.gif?imgmax=800)
![clip_image008[12] clip_image008[12]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5XoG4ClI/AAAAAAAAET4/ut544q8IKvc/clip_image008%5B12%5D_thumb.gif?imgmax=800)
![clip_image010[10] clip_image010[10]](http://lh4.ggpht.com/_Qmjqb2Gk9no/S3q5YgxPIAI/AAAAAAAAEUA/B1BguHr6idQ/clip_image010%5B10%5D_thumb.gif?imgmax=800)
![clip_image012[8] clip_image012[8]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5Z0Dn9XI/AAAAAAAAEUI/800pPdtg1wU/clip_image012%5B8%5D_thumb.gif?imgmax=800)
![clip_image014[8] clip_image014[8]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q5bHIzelI/AAAAAAAAEUQ/9PQ28uGjdo0/clip_image014%5B8%5D_thumb.gif?imgmax=800)
![clip_image016[4] clip_image016[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5cfXdo3I/AAAAAAAAEUY/NUwRESUaRqc/clip_image016%5B4%5D_thumb.gif?imgmax=800)
![clip_image030[4] clip_image030[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5nIYe2jI/AAAAAAAAEVQ/GU77nHaKR98/clip_image030%5B4%5D_thumb.gif?imgmax=800)
![clip_image032[4] clip_image032[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5oaxtyaI/AAAAAAAAEVY/foZUEFPTnr4/clip_image032%5B4%5D_thumb.gif?imgmax=800)
![clip_image034[4] clip_image034[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5psTMfBI/AAAAAAAAEVg/mdXEM3ZK8DQ/clip_image034%5B4%5D_thumb.gif?imgmax=800)
![clip_image036[4] clip_image036[4]](http://lh4.ggpht.com/_Qmjqb2Gk9no/S3q5rG8JV2I/AAAAAAAAEVo/AyXoDdZVWcU/clip_image036%5B4%5D_thumb.gif?imgmax=800)
![clip_image038[4] clip_image038[4]](http://lh5.ggpht.com/_Qmjqb2Gk9no/S3q5sBJmoiI/AAAAAAAAEVw/xY9BIznSVMQ/clip_image038%5B4%5D_thumb.gif?imgmax=800)
![clip_image040[4] clip_image040[4]](http://lh6.ggpht.com/_Qmjqb2Gk9no/S3q5t4z4P7I/AAAAAAAAEV4/b6EutJOS-G0/clip_image040%5B4%5D_thumb.gif?imgmax=800)

Não tinha ouvido falar destas propriedades ainda... Obrigado por divulgar!
ResponderExcluirUm abraço!
São somente para formatos espeíficos, geralmente estudados em cursos de Álgebra. Mas é sempre bom divulgar!
ResponderExcluirAbraços!
Esta eu coloquei no favoritos porque também não sabia. É raro de se ver em livros.
ResponderExcluirEsse post foi herança do meu curso de graduação. Tinha um professor de Álgebra (Mário Biague) que dava aulas com livros russos. Uma peça! O cara falava russo, húngaro, inglês, espanhol e português!
ResponderExcluirAbraços.
Eu conheço este professor, ele é africano tem dupla nacionalidade, um da Guiné-Bissau e outro da Russia, ele não fala russo, húngaro, inglês, espanhol, português também ele fala crioulo e mancanhe.
ExcluirEste professor ( Mário Biague ) ele conhece matemática muito bem, tive oportunidade de apertar mão de ele e ficar cara a cara com ele.
ExcluirA primeira identidade aparece na resolução de equações de 3º grau.
ResponderExcluir