Em alguns livros ou mesmo na internet, tratam estas funções como Divisão de Arcos ou como Arco Metade. Decidi chamar de semi-arco, pelo fato desta demonstração ser de uma arco dividido por 2. Vejamos:
Da relação trigonométrica fundamental [veja aqui], temos que:
Para um ângulo qualquer, até mesmo para a metade de θ, a relação (1) continua válida e podemos representar como:
Podemos expressar θ como:
E podemos expressar cos(θ) como:
Mas, como:
Logo termos:
Da relação (2), temos:
Substituindo (6) em (5), obtemos:
Sabemos pela relação (4) que:
Da relação trigonométrica fundamental, dada em (2), temos:
Substituindo a relação (9) em (8), obtemos:
A tangente de um ângulo é dada pela divisão entre o seno e o cosseno deste ângulo, representamos por:
Então, para a tangente do semi-arco, teremos:
Substituindo os valores já determinados para o seno e o cosseno de semi-arcos dados em (7) e (10) na relação (11), obtemos:
Veja mais:
Demonstração da Adição e Subtração de Arcos
Demonstração das Funções Trigonométricas do Arco Duplo
Demonstração da Relação Trigonométrica Fundamental



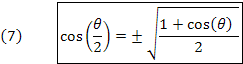
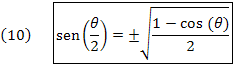
![clip_image002[6] clip_image002[6]](http://lh6.ggpht.com/_Qmjqb2Gk9no/TDHAkE_8PvI/AAAAAAAAIws/RlzkQY8lC8U/clip_image002%5B6%5D_thumb.gif?imgmax=800)
![clip_image002[4] clip_image002[4]](http://lh4.ggpht.com/_Qmjqb2Gk9no/TDHAlAUCZjI/AAAAAAAAIw0/5i_uP49kKFc/clip_image002%5B4%5D_thumb.gif?imgmax=800)
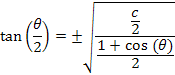
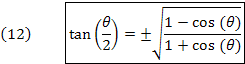

A fórmula (10) não seria sen(theta/2)?
ResponderExcluirAbraços,
Ops...falha minha. Corrigido. Obrigado por avisar!
ResponderExcluirMuito boa a explicação !Meus parabéns.
ResponderExcluir