Organograma dos Quadriláteros Notáveis

Vi em um blog um organograma dos quadriláteros notáveis. Achei muito interessante e resolvi fazer um post. No entanto, achei que precisaria expor suas características e propriedades para melhor compreensão. As devidas demonstrações farei em outra oportunidade.

Quadriláteros

Quadrilátero é um polígono simples de quatro lados. Estes podem ser côncavos ou convexos.

Em um quadrilátero há sempre duas diagonais e a soma dos ângulos internos é sempre igual a 360° (S_i = 360°), assim como a soma dos ângulos (S_e = 360°).

Interessamo-nos especialmente pelos quadriláteros convexos, pois alguns deles possuem propriedades tão especiais que são chamados de quadriláteros notáveis, que podem ser: Trapézios, Paralelogramos, Retângulos, Losangos e Quadrados.

Trapézio

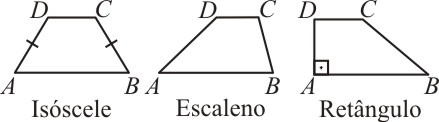
Um quadrilátero plano convexo é um trapézio se, e somente se, possui dois lados paralelos:

Os lados paralelos são as bases do trapézio e, a partir dos outros lados, podemos defini-lo como:

· Trapézio Isóscele: se estes lados são congruentes;

· Trapézio Escaleno: se estes lados não são congruentes;

· Trapézio Retângulo: se o trapézio tem dois ângulos retos.

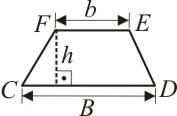
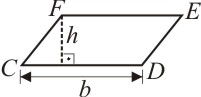
Os elementos de um trapézio são:

b é a base menor;

B é a base maior;

h é a altura (distância entre as bases).

A área de um trapézio é dada por:

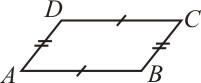
Paralelogramo

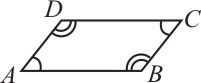
Um quadrilátero plano convexo é um paralelogramo se, e somente se, possui os lados opostos paralelos.

Nos paralelogramos podemos verificar as seguintes propriedades:

· Em todo paralelogramo dois ângulos opostos quaisquer são congruentes:

· Em todo paralelogramo dois lados opostos quaisquer são congruentes:

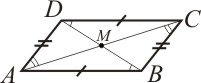
· Em todo paralelogramo as diagonais interceptam-se nos respectivos pontos médios:

Os elementos de um paralelogramo são:

b é a base;

h é a altura.

A área do paralelogramo é dada por:

Vejam que, se o paralelogramo tiver as diagonais congruentes, este será um retângulo; Se o paralelogramo tiver suas diagonais perpendiculares, este será um losango; Agora, se o paralelogramo tiver as diagonais congruentes e perpendiculares entre si, este será um quadrado!

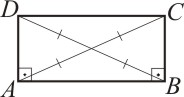
Retângulo

Um quadrilátero plano convexo é um retângulo se suas diagonais forem congruentes:

Todo paralelogramo que tem diagonais congruentes é um retângulo:

Os elementos de um retângulo são:

a é a medida de dois lados paralelos;

b é a medida dos outros dois lados paralelos.

A área do retângulo é dada por:

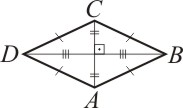
Losango

Um quadrilátero plano convexo é um losango se suas diagonais forem perpendiculares:

Todo paralelogramo é um losango se suas diagonais forem perpendiculares:

Os elementos de um losango são:

d é a diagonal menor;

D é a diagonal maior.

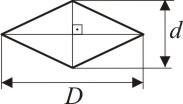
A área do losango é dada por:

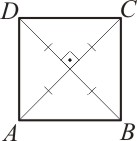
Quadrado

Um quadrilátero plano convexo é um quadrado se suas diagonais forem perpendiculares e congruentes:

Veja que o quadrado possui as propriedades do retângulo e do losango juntas.

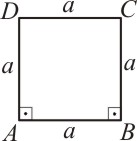
Os elementos do quadrado são:

a é a medida dos lados.

A área do quadrado é dada por:

Veja abaixo o organograma dos quadriláteros:

[Clique na imagem para aumentar]

Referências:

[1] Fundamentos de Matemática Elementar, Vol 9 – Geometria Plana – Osvaldo Dolce
[2] Matemática Volume Único – Facchini
[3] Matemática Volume Único – Benigno Barreto Filho

---

Veja mias:

Diagrama de Venn dos Quadriláteros Notáveis
Classificação dos Sistemas Lineares
Quadriláteros Notáveis

---