 Vimos no primeiro post sobre o número prateado, uma breve introdução que o traz como algo novo, curioso, com grande potencial a ser explorado, mas sem muito formalismo. Neste post, veremos que esta constante também está relacionada à Trigonometria, nas funções seno, cosseno e tangente.
Vimos no primeiro post sobre o número prateado, uma breve introdução que o traz como algo novo, curioso, com grande potencial a ser explorado, mas sem muito formalismo. Neste post, veremos que esta constante também está relacionada à Trigonometria, nas funções seno, cosseno e tangente.
Vamos provar através da trigonometria e álgebra básica que:
Da Trigonometria, sabemos que:
Se considerarmos, por exemplo, um valor para θ = π / 8 = 22,5°, temos que:
Multiplicamos o numerador e o denominador por (2 + √2):
Pela definição do número prateado, temos que:
Substituindo na equação acima, encontramos:
Extraímos a raiz de ambos os membros relação acima:
Da relação trigonométrica fundamental, temos que:
Para θ = π / 8:
Substituímos a relação (2) na relação (3):
Pela definição do número prateado temos que:
Substituindo na relação acima, temos:
Extraindo a raiz:
Podemos ainda determinar a tangente de π / 8:
Substituímos os valores (2) e (4) em (5), obtendo:
O desenvolvimento das demonstrações foram feitas pelo Professor Paulo do blog Fatos Matemáticos, que gentilmente me cedeu o material para publicar aqui neste blog.
Vejam mais:
O Número Prateado
O Número Prateado e a Área do Octógono Regular
Algumas Propriedades do Número Prateado no blog Fatos Matemáticos


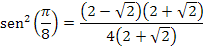
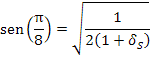
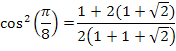
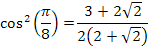
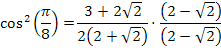
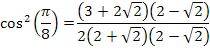


Olá, Kleber!
ResponderExcluirQue bom! Vejo que esse Número Prateado em termos de interesse, de desconhecido que era, já está superando a procura das aplicabilidade, do Número de Ouro. Você e o professor Paulo, estão de parabéns pelo ótimo post!
Um abraço!!!!!
Olá Valdir, pois é... ainda não sabemos direito o seu potencial. O pouco do material que tem está em inglês e espanhol e os estudos são muito superficiais. O Paulo deu uma bela demonstrada aqui. Eu dei umaformatada e introduzi algumas passagens. Tenho mais um material aqui, flata digitar e fazer as figuras, em brevepublico.
ResponderExcluirUm abraço!