Esta é uma construção com três circunferências concêntricas, cujos raios estão numa proporção de 1 : 2 : 4, onde podemos encontrar a razão áurea:
Sejam três circunferências concêntricas de raios 1, 2 e 4. Traçar uma tangente à circunferência menor em C, marcando os pontos A e B na circunferência de raio 2 e D na circunferência externa.
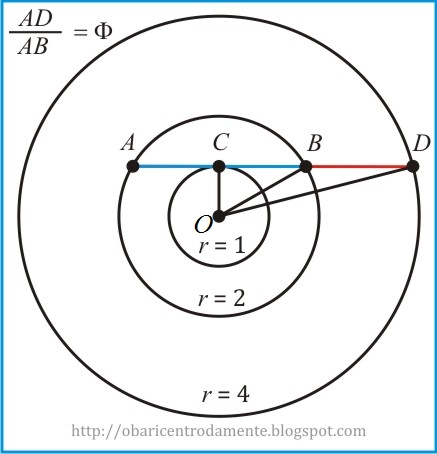 A razão entre os segmentos AD e AB é PHI e pode ser provada da seguinte forma:
A razão entre os segmentos AD e AB é PHI e pode ser provada da seguinte forma:
No triângulo OCB, retângulo em C, aplicamos o teorema pitagórico:
Então o segmento AC medirá:
e
No triângulo OCD, analogamente, encontramos a medida do segmento CD:
Logo, o segmento AD medirá:
A razão entre os segmentos AD e AB:
Esta construção foi desenvolvida por Sam Kutler e apresentada por Steve Lautizar.
Veja mais:
Construção Geométrica de PHI em Circunferências (Parte 1)




Muito bonita esta construção e phi, apenas faltou o ponto O, mas subentende-se que ele é o centro das circunferências. Parabéns pelo post.
ResponderExcluirAs construções que envolvem PHI sempre são muito belas. Corrigido centro $O$!
ResponderExcluirOlá, Kleber!
ResponderExcluirPhiquei pasmo em apreciar, tamanha demonstração de precisão e simplicidade para se obter o valor de phi.
Também phiquei pensando se... e pergunto: precisamos sempre usarmos o conjunto de três circunferências na construção geométrica para obtermos o valor de PHI?
Parabéns, pela postagem!
Um abraço!!!!!
Olá Valdir, na verdade foi pura coincidência as duas primeiras partes serem com 3 circunferências. Mas que é bonito de se ver, isso é!
ResponderExcluirUm abraço!
Interessante resolução. Fico pensando o que o matemático não é capaz de fazer.Parabéns pelo blog!
ResponderExcluir