Medida confiável é sempre duvidosa, desde que não empreguemos ferramentas necessárias para sua medição. Às vezes não basta um bom instrumento de medição e neste caso a Matemática pode nos ajudar.
A necessidade de fazer medições faz parte de nosso dia a dia desde a mais tenra idade. Quando um bebê joga a bola para a mãe, ele faz uma estimativa visual da distância e direção do seu arremesso. Esse processo é intuitivo, não científico, e não envolve a comunicação de uma medida.
O relógio, a fita métrica, o termômetro e a balança são instrumentos de medição que fazem parte de nosso cotidiano.
Quando a medição exige maior exatidão, procuramos utilizar um instrumento e uma medida padrão: torna-se necessário o uso de algum rigoroso método em que se considere o erro de medição.
Nas pesquisas científicas, a medição é um processo que envolve ações experimentais para determinar os valores associados a uma ou várias grandezas. No entanto, por mais que se tenham cuidados e critérios nos procedimentos adotados para fazer uma aferição, o resultado nunca é considerado exato: ele é sempre avaliado como o valor mas provável da grandeza aferida.
De fato, toda medida é passível de erro. Embora a meta seja não errar, o pesquisador nunca estará certo de que nenhum tipo de erro tenha sido cometido. Os erros podem ser provocados por diversos fatores, por mais competente que seja o pesquisador e por melhor que seja o instrumento de medição por ele adotado.
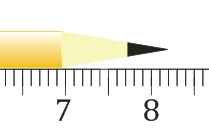
Vamos utilizar o exemplo a seguir para ilustrar a incerteza de uma medição: Ao medir um lápis com uma régua graduada em centímetros, não se tem a certeza do valor em milímetros; e se usar uma régua graduada em milímetros, a incerteza será em relação ao valor em milésimo de milímetro!
 Observando a figura acima, vemos que a medida é um valor entre 8,2 cm e 8,3 cm. Mesmo que seja ampliada a ponta do lápis, ainda permanece a incerteza: o lápis mede 8,24 cm, 8, 25 cm ou 8,26 cm? O centésimo, nesse caso é sempre um valor duvidoso.
Observando a figura acima, vemos que a medida é um valor entre 8,2 cm e 8,3 cm. Mesmo que seja ampliada a ponta do lápis, ainda permanece a incerteza: o lápis mede 8,24 cm, 8, 25 cm ou 8,26 cm? O centésimo, nesse caso é sempre um valor duvidoso.
 Se, além disso, em determinado momento o experimentador observa a medida, posicionado a certo ângulo de visão do objeto que está medindo, por exemplo, e instantes depois faz uma nova observação sob um ângulo diferente, a estimativa feita na segunda situação poderá ser diferente da primeira.
Se, além disso, em determinado momento o experimentador observa a medida, posicionado a certo ângulo de visão do objeto que está medindo, por exemplo, e instantes depois faz uma nova observação sob um ângulo diferente, a estimativa feita na segunda situação poderá ser diferente da primeira.
Como regra para a escrita do valor encontrado para uma medida, sempre se colocam todos os algarismos de que se tem certeza, mais um algarismo duvidoso. Retomando a medida do lápis, os algarismos 8 e 2 são garantidos, porém o algarismo do centésimo e duvidoso. Ao escrever esta medida, não seria correto colocar 8,2 cm (o algarismo duvidoso seria o 2) ou 8,241 cm (o algarismo duvidoso seria o 1).
Para aumentar a confiabilidade do valor estimado, uma medição é repetida por diversas vezes, sob as mesmas condições, registrando-se em forma de tabela ou gráficos todos os valores obtidos.
O valor mais provável será dado pela média aritmética de todos os valores obtidos. Definimos ![]() como média aritmética:
como média aritmética:
Por ser um valor provável, e não real, é preciso considerar a variação que ele pode ter, ou seja, conhecer os desvios de medição. Para isso, um procedimento comum no tratamento matemático das medidas é calcular a média dos módulos de todos os desvios da medida, denominado por desvio absoluto médio:
O registro da medida será dado por:
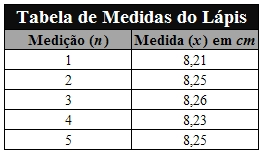
Vamos utilizar novamente o exemplo do lápis, considerando apenas cinco medições:
Agora, calculamos o desvio absoluto médio:
Podemos arredondar este valor para duas casas decimais obtendo:
Então, a forma de escrita da medida do lápis se completa:
O significado desse resultado é: o valor mais provável da série de cinco medições do tamanho do lápis é 8,24 cm podendo haver variações no intervalo de 8,22 cm a 8,26 cm.
Veja mais:
Regressão Linear
Regressão Polinomial
As 7 Unidades de Base do S.I.



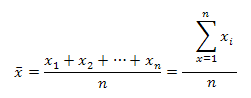

Excelente a postagem, meus parabéns.
ResponderExcluirOlá Prof. Fernando,
ResponderExcluirRealmente é uma ferramenta simples e que resolve um problema de medição: "quanto" é o suficiente? Basta fazermos algumas medições, coletar amostras e aplicar a fórmula. Assim obtemos uma ótima precisão.
Obrigado pelo comentário.