Neste post, vamos observar um exemplo de como as matrizes podem servir de modelos para descrever situações de nosso dia a dia.
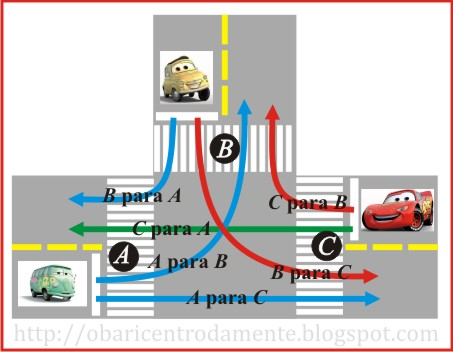
A figura abaixo representa um cruzamento de duas ruas de mão dupla, cujo fluxo de automóveis nos pontos A, B e C é definido por três conjuntos de semáforos.
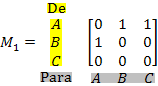
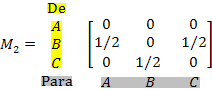
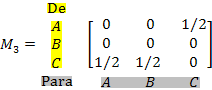
As matrizes M1, M2 e M3 indicam o tempo, em minutos, durante o qual os semáforos se mantêm simultaneamente abertos segundo a sequência dada:
Inicialmente, durante 1 minuto, ficam verdes os semáforos de A para B, de A para C e de B para A.
Em seguida, durante meio minuto, ficam verdes os semáforos de B para A, de B para C e de C para B.
E, finalmente, durante meio minuto, ficam verdes os semáforos de C para A, de C para B e de A para C.
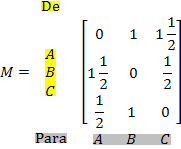
A matriz M é obtida somando-se M1, M2 e M3 termo a termo e mostra o tempo que cada semáforo fica aberto em cada sentido no período de 2 minutos.
Podemos observar, por exemplo, que o semáforo de B para A fica aberto durante 1 minuto e meio a cada período de 2 minutos.
Se multiplicarmos todos os termos da matriz M por 30, já que o período é de 2 minutos, obteremos o tempo, em minutos, que cada semáforo fica aberto durante 1 hora.
Neste exemplo hipotético, sabe-se que nestas ruas é possível passar até 20 carros por minuto cada vez que os semáforos abrem. Assim, se multiplicarmos por 20 todos os termos da matriz N, teremos a quantidade máxima de carros que podem passar por este cruzamento no período de 1 hora.
Se o número de carros em alguma das direções for maior que a quantidade máxima possível, teremos um engarrafamento, que poderá ou não ser resolvido alterando-se os tempos de abertura dos semáforos, isto é, modificando-se os valores das matrizes M1, M2 e M3.
Referências
[1] Matemática Ensino Médio V1 – Stocco Smole e Diniz
Veja mais:
Matrizes de Rotação no R2
Cayley e a Teoria das Matrizes
O Método de Castilho para Resolução de Sistemas Lineares


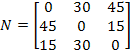
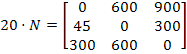

Isso é realmente incrível, as matrizes são ferramentas poderosas nessas situações que envolvem sistemas dinâmicos, o artigo ficou ótimo.
ResponderExcluirOlá, Kleber!
ResponderExcluirEu já li há muito tempo, quando tive conhecimento da existência dos quadrados mágicos que, segundo parece, seria uma invenção chinesa, que disseram... suponho que foi ou foram os seus criadores, o fato é, teriam dito: "quando o homem descobrisse o real poder dos quadrados mágicos... os tempos da fortuna e da felicidade cobririam o mundo"! Para mim, um quadrado mágico é uma matriz e a matriz que não é um quadrado mágico (como essa aí, embora seja uma matriz quadrada) nem por isso deixa de ter uma utilidade para resolver e bem, os problemas das nossas atividades e eis aí... a felicidade. E a fortuna...? Eu perguntaria ao Bill Gattes se o Excel lhe proporcionou alguma! Voce concorda?
Muito boa, essa sua postagem sobre o emprego de matrizes e... meus parabéns!
Um abraço!!!!!
eu sei
ExcluirOlá pessoal.
ResponderExcluirUma matriz milionária para o Sr. Gates!
Realmente as matrizes são muito dinâmicas e por isso são utilizadas em diversos ramos das ciências. Como deve ser o controle dos semáforos, por exemplo, na cidade de são paulo?
Vi uma palestra de um matemático que trabalha no metrô, que para incluirem uma nova linha, é feito um trabalho intenso de pesquisa. É discutido a origem e destino, horários de picos e tudo o mais. Isso gerava uma matriz imensa, com n linhas e colunas. Foi uma pena não terem fornecido nenhum material escrito.
Um abraço amigos!
muito legal nem sabia que as matrizes seria tão importante ainda no controle de transito (:
ResponderExcluirOlá, Kleber!
ResponderExcluirQue ótima aplicação heim!
E ainda tem gente que dirá que é só um exemplo particular. E fala um monte de asneira.
Um abraço!
Olá Edigley!
ExcluirRealmente é fascinante! Este é um exemplo simples, sem considerar sinal para pedestres e outras conversões.
O problema desse pessoal que só sabe falar mal é a incapacidade de pensar.
Agradeço seu comentário.
Um abraço!