 Em busca de uma solução para o problema da quadratura do círculo, muitas construções já foram dadas para obter um segmento de reta de comprimento aproximado a π.
Em busca de uma solução para o problema da quadratura do círculo, muitas construções já foram dadas para obter um segmento de reta de comprimento aproximado a π.
Este método de retificação foi desenvolvido por Gelder, mas somente publicada em 1849, 1 ano após sua morte.
Jacob de Gelder (1765 – 1848) foi um matemático holandês que serviu de inspiração para uma nova compreensão da finalidade e aplicação da matemática no início do século XIX na Holanda.
Gelder iniciou sua carreira em 1790 em Rotterdam, como professor em Wiskunst. Suas primeiras publicações datam de 1791 e 1794. Foi muito influente sobre questões de educação e a matemática passou a ser parte obrigatória do currículo de cada curso com um apelo ao valor educativo.
Aposentou-se aos 75 anos e no mesmo ano de 1840, recebeu o prêmio de Cavaleiro da Ordem do Leão Holandês. Faleceu em 1848 após uma rápida doença.
Vamos ver como se dá a construção de Gelder para o problema da retificação e determinar uma aproximação para π com precisão de 6 casas decimais. O que é curioso neste método é que o segmento construído aproxima somente a parte decimal de π.
A Retificação:
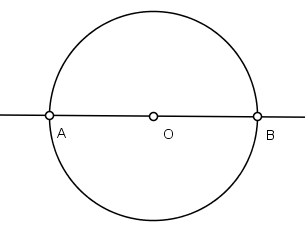
Seja AB o diâmetro de uma circunferência de diâmetro igual a 1:
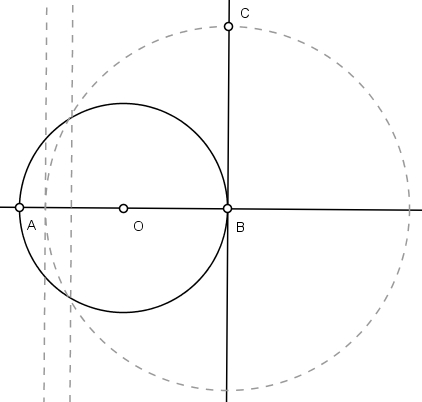
 Trace o segmento BC = 7/8 do diâmetro, perpendicular a AB em B:
Trace o segmento BC = 7/8 do diâmetro, perpendicular a AB em B:
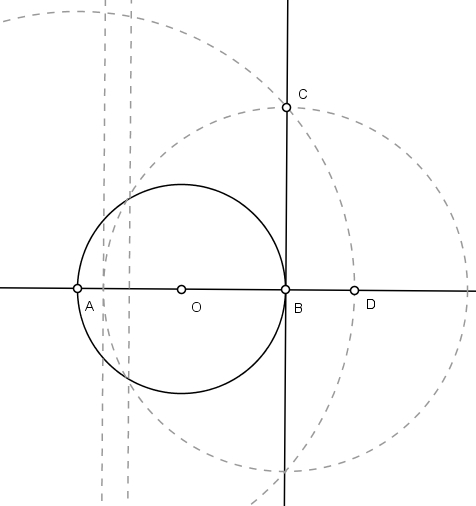
 No prolongamento de AB, marque AD = AC. Para isso, descreva um arco de raio AC e centro em A:
No prolongamento de AB, marque AD = AC. Para isso, descreva um arco de raio AC e centro em A:
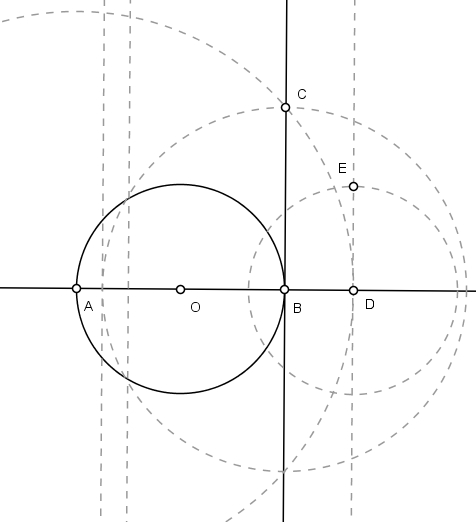
 Trace DE = 1/2, perpendicular a AD em D.
Trace DE = 1/2, perpendicular a AD em D.
 Trace o segmento AE e seja F o pé da perpendicular a AC por D:
Trace o segmento AE e seja F o pé da perpendicular a AC por D:
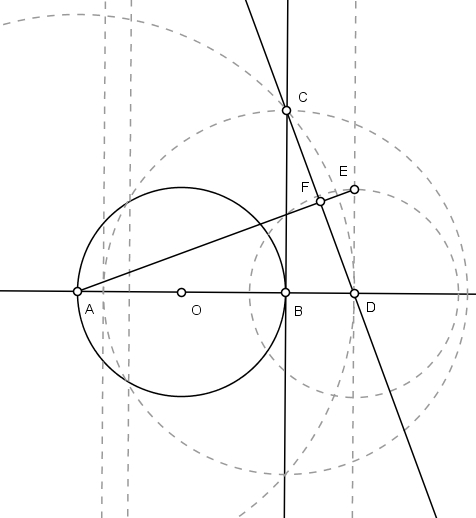 Una os pontos BF e trace uma paralela por E. Marque como G a intersecção com BD:
Una os pontos BF e trace uma paralela por E. Marque como G a intersecção com BD:
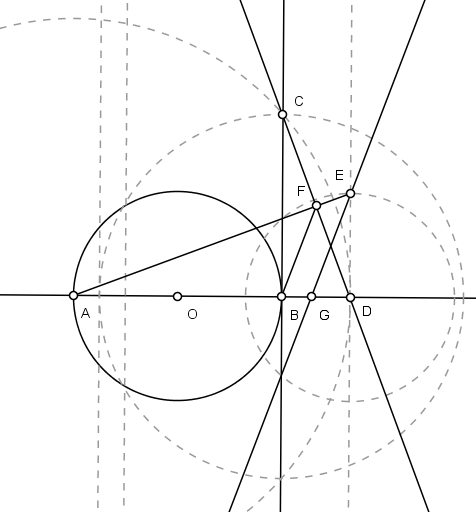 O segmento BG é aproximadamente a parte decimal de π, com precisão até a sexta casa decimal.
O segmento BG é aproximadamente a parte decimal de π, com precisão até a sexta casa decimal.
Demonstração:
Nos triângulos GAE e BAF, temos os segmentos proporcionais:
Como o triângulo ABC é retângulo em B, temos que:
Mas AC = AD, logo:
Substituímos (3) em (1):
No entanto, AB = 1, DE = 1/2 e BC = 7/8. Substituímos estes valores na relação (4):
Assim, obtemos o valor da parte decimal de π com 6 casas decimais corretas. Para o valor de π, somamos sua parte inteira:
Para a construção geométrica, já temos o segmento BG = 0,1415929 e o segmento AB = 1. No prolongamento do segmento BA, fazemos dois arcos de raios igual a AB: um de centro em A marcando H e outro de centro em H marcando I. Assim, o segmento IG aproxima π.
Referências:
[1] Introdução à História da Matemática – Howard Eves
[2] http://bwnw.cwi-incubator.nl/
Veja mais:
Retificação da Circunferência (Parte 1)
Retificação da Circunferência (Parte 2) - Método de Kochanski
Uma Breve Cronologia de PI


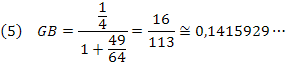

Olá, Kleber!
ResponderExcluirNão conhecia esse trabalho! Caramba! Eu faço algumas maluquices como essa, muitas das vezes, são redescobertas e sei que... nessas horas, o pesquisador e/ou inventor, fica mergulhado em uma atmosfera estranha, digo isto por experiência própria, portanto... amei saber do poder criativo do Gedel demonstrado ao inventar esse método!
Parabéns, para você por resgatar, através de mais um de seus trabalhos de postagens de ótimas qualidades editoriais e educacionais, as informações biográficas e também, desse trabalho do Gedel. Show de bola!
Um abraço!!!!!
É verdade Valdir, este foi um feito! $\pi$ com seis casas decimais!
ResponderExcluirA biografia de Gedel é muito escassa. Encontrei somente num site holandês e mesmo lá tem muito pouca informação.
Entendo você perfeitamente quando diz que ficamos em elucubrações. Eu gosto bastante de construções geométricas e estou tentando alguma para aproximar $pi$ com boa aproximação. Mas até agora só consegui no máximo com 1 casa decimais. Vou tentando, quem sabe chego lá.
Abraços amigo!