Existem vários fatores evolutivos responsáveis por alterações nas frequências gênicas da população. Os principais fatores considerados pela teoria sintética da evolução são: mutação, permutação, migrações, seleção natural e deriva genética.
[Hardy & Weinberg]
Vamos primeiramente aprender a calcular as frequências gênicas e genotípicas das populações e depois analisar uma das maneiras pelas quais ocorre o processo de especiação.
A composição genética de uma população pode ser conhecida calculando-se as frequências de genes e as frequências de genótipos nessa população.
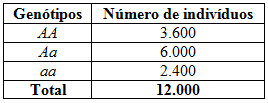
Vamos determinar como exemplo, a frequência gênica e a genotípica de uma população que apresenta as seguintes características:
A frequência dos alelos A ou a nessa população pode ser calculada assim:
A frequência do alelo A é:
O número total de alelos na população para esse lócus é de 24.000, pois são 12.000 indivíduos diplóides, cada um com dois alelos para o lócus em questão:
Para calcular a frequência de a, podemos proceder da mesma forma ou utilizar a fórmula que estabelece a relação entre os alelos:
Aplicando os valores na fórmula 1, obtemos:
Nessa hipotética população, as frequências dos alelos A e a são, portanto, respectivamente iguais a:
A frequência genotípica nesse caso pode ser calculada do seguinte modo:
As frequências do genótipos AA, Aa e aa nessa população são, respectivamente:
Neste exemplo, o número de indivíduos e a distribuição dos genótipos para determinado par de alelos são conhecidas. A partir dessa população, ou de qualquer outra, pode-se estimar a frequência gênica e a genotípica da geração seguinte com base no teorema de Hardy-Weinberg.
Levando em conta a genética das populações, considera-se que uma determinada população está em equilíbrio quando seu estoque gênico (pool) permanece inalterado ao longo das gerações. Por outro lado, uma das populações encontra-se em evolução quando seu pool gênico vai se modificando através das gerações.
A existência ou não de alterações no pool gênico de uma população pode ser constatada por meio de métodos matemáticos que permitem determinar as frequências gênicas que ocorrem nessa população.
Em 1908, Godfrey Harold Hardy (1877 – 1947), matemático inglês, e Wilhelm Weinberg (1862 – 1937), físico alemão, descobriram, independentemente, O Princípio da Constância da Frequência Gênica e Genotípica para uma população em equilíbrio. O teorema formulado pode ser enunciado assim:
Teorema: Em uma população infinitamente grande, em que os cruzamentos ocorrem ao acaso e sobre a qual não há atuação de fatores evolutivos, as frequências gênicas e genotípicas permanecem constantes ao longo das gerações.
Esse teorema também é conhecido como Equilíbrio de Hardy-Weinberg, somente é válido para populações em equilíbrio quando estas:
1) Abrigarem um número de indivíduos infinitamente grandes. Isso quer dizer que o número de indivíduos da população seja grande o suficiente, onde os eventuais erros de amostragem no processo de levantamento das frequências gênicas ou genotípicas não tiverem significado estatístico;
2) Forem panmíticas (panmítica: pan=todos; mítica=misturar), isto é, seus integrantes se cruzam livremente, ao acaso, e sem preferências sexuais;
3) Estiverem isentas de fatores evolutivos, como mutação, seleção natural e migrações, livres de qualquer fator que promova alteração no pool gênico.
A importância do teorema de Hardy-Weinberg para as populações naturais está no fato de ele estabelecer um modelo para o comportamento dos genes. Assim, é possível estimar frequências gênicas e genotípicas ao longo das gerações e compará-las com as obtidas na prática.
Se os valores observados forem significativamente diferentes dos valores esperados, pode-se concluir que fatores evolutivos estão atuando sobre esta população e que ela está evoluindo. Se os valores não diferirem significativamente, pode-se concluir que a população está em equilíbrio e, portanto, não está evoluindo.
Vamos considerar um gene A, de frequência p; e seu alelo recessivo (a), de frequência q. Na população considerada:
Vamos supor que esta população abrigue indivíduos AA (formadores de gametas A), aa (formadores de gametas a) e Aa (formadores de gametas A e a). Podemos concluir que, para surgir um indivíduo de genótipo AA, é preciso que o gameta masculino seja A e o gameta feminino seja A. Lembrando que a frequência do gene A( f(A)) = p, temos:
Da mesma forma, o surgimento de indivíduos de genótipo aa implica a existência de um gameta masculino a e outro feminino a. Assim, lembrando que f(a) = q, temos:
Para o surgimento de indivíduos Aa, entretanto, pode-se ter um gameta masculino A e outro feminino a vice-versa. Logo, existem duas possibilidades para a ocorrência de indivíduos Aa. Assim, temos:
Note que:
Então, podemos considerar que:
Nessa representação, p é a frequência de um alelo e q é a frequência do outro alelo. Nesta fórmula, p2 e q2 representam as frequências dos homozigotos para um e outro alelo, 2pq representa a frequência dos heterozigotos.
Exemplo 1: Uma população tem as seguintes frequências gênicas:
- p = frequência do alelo B = 0,9. Portanto, a frequência esperada de B e B (BB) é p2 = 0,81;
- q = frequência do alelo b = 0,1. Portanto, a frequência esperada de b e b (bb) é q2 = 0,01;
- Os heterozigotos correspondem a B e b ou b e B, sua frequência na população é dada por 2pq = 0,18.
Assim:
Se a população estiver em equilíbrio, a frequência dos alelos e dos genótipos se manterá constante ao longo das gerações. Se, no entanto, verificarmos que os valores obtidos na prática para os genótipos são significativamente diferentes dos esperados, a população não se encontra em equilíbrio genético e, portanto, está evoluindo.
Exemplo 2: Numa dada população humana em equilíbrio, determinou-se que a frequência de indivíduos Rh – era de 16%. A partir dessa informação, determine:
a) A frequência do gene r;
b) A frequência do gene R
c) A frequência dos indivíduos Rh + homozigotos (RR) e heterozigotos (Rr).
Resolução:
a) Sabendo que os indivíduos Rh – exibem genótipo RR, temos que:
Logo, a frequência do gene r (f(r)):
b) Como q = f (r) = 0,4, temos que a frequência do gene R (f(R)) é dada por:
c) Sabendo que q = 0,4 e p = 0,6, a frequência dos indivíduos RR será:
Da mesma maneira, a frequência dos indivíduos Rr, será:
Observe que:
O Teorema de Hardy-Weinberg não se aplica com exatidão plena a populações naturais que estão sujeitas, por exemplo, a efeitos da seleção natural, de mutações e até mesmo de uniões sexuais até certo ponto preferenciais. Mas como modelo é importante, pois facilita a pesquisa da composição de uma população em termos de frequência gênica; a investigação dos efeitos da seleção natural sobre a composição genética de uma população; a determinação de genótipos, mesmo quando não são reconhecidos fenotipicamente.
As populações humanas estão evoluindo? Como exemplo, podemos analisar nos últimos anos a taxa do gene para a hemofilia. Estes têm aumentado muito nas populações humanas. Isso é fácil de entender: os hemofílicos, no passado, frequentemente não chegavam à idade de reprodução, já que para eles qualquer ferimento maior poderia ser fatal.
Hoje, porém, os hemofílicos recebem o fator VIII, retirado do sangue de pessoas normais, que favorece a coagulação. Assim, a probabilidade de sobrevivência dos hemofílicos aumentou muito; também se elevaram as chances de constituírem família, transmitindo seus genes para os descendentes.
Nesse caso, os avanços da medicina modificaram a atuação da seleção natural, fator que, no passado, mantinha o gene para a hemofilia em taxa baixa.
Referências:
[1] Biologia Volume Único – César e Sezar
[2] Biologia Volume Único – Sônia Lopes e Sergio Rosso
[3] Biologia Volume 3 – Genética, Evolução e Ecologia – Wilson Roberto Paulino
Veja mais:
No Cerne do ENEM, o Teorema de Bayes
EDO: Naftalina e o Tempo de Sublimação
A Equação de Siple e a Perda de Calorias



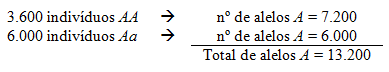
![clip_image002[53] clip_image002[53]](http://lh6.ggpht.com/-iRCTF4-2NIw/Tvt8y8EfTdI/AAAAAAAAQJ4/VaVQEDxtbLQ/clip_image002%25255B53%25255D_thumb.gif?imgmax=800)

Viajei no tempo lendo esse artigo. Voltei ás aulas de Biologia no Ensino Médio...
ResponderExcluirTodo dia fico surpreso em ver como a Matemática se faz presente em diversos campos da Ciência. Eu me sinto maravilhado e ao mesmo tempo espantado.
Excelente artigo Kleber.
Abraço!
Olá Ed,
ResponderExcluirObrigado pelos elogios. Olha como as coisas são engraçadas: estou de férias com minha esposa e filha no litoral na casa de meus sogros. Minha sogra e professora de biologia e estava se desfazendo de vários livros. Por acaso comecei a folhear alguns e me deparei com este teorema. Procurei nos outros livros e um complementava o outro. Acho que ficou bem legal. Tive que relembrar alguns conceitos, como homozigotos, alelos, locus,... o que achei interessante é que esse teorema foi formulado por matemático e físico e não por biólogos. Mas a matemática é mágica e creio que não haja um ramo das ciências em que ela não se aplique. Temos que ficar atentos para um post em potencial quando lermos qualquer livro.
Um grande abraço.
Obrigada Kleber, vou fazer uma prova de melhoramento genético e seu artigo me ajudou muito, se soubermos procurar, a internet pode ser uma excelente ferramenta de estudo! Parabéns!
ResponderExcluir