Karl Raimund Popper (1902 - 1994), foi um filósofo austríaco naturalizado britânico, talvez um dos mais influente do século XX. Em sua obra polêmica anti-Platão: A Sociedade Aberta e seus Inimigos, Popper especula se Platão em seu período de desenvolvimento dos sólidos platônicos, teria escolhido triângulos como componentes básicos de sua teoria como tentativa de proporcionar uma base matemática para todos os números possíveis, podendo, assim, construir segmentos com medidas 1, raiz de 2, raiz de 3, π, etc.
Popper, baseado no fato de que raiz de 2 mais raiz de 3 é aproximadamente π, especula se Platão teria pensado que π poderia ser expresso como a soma das raízes de 2 e 3, o que não deve ser verdade, pois se assim fosse, estaria resolvida a questão da quadratura do círculo.
Já sabemos que o número π é impossível de ser representado sob forma de fração entre números inteiros, assim como sua retificação, um problema estudado durante séculos. Uma forma elegante de aproximar π é utilizar a soma:
Vamos ver uma construção geométrica onde podemos obter um segmento com esta medida.
Construção
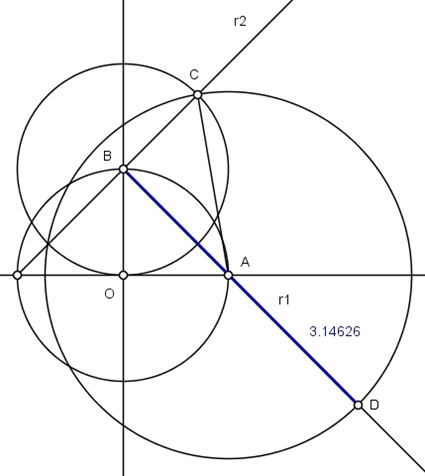
1) Comece descrevendo uma circunferência de raio r = 1 com centro O num eixo ortogonal de coordenadas. Trace a semirreta r1 passando pelos ponto A e B. O comprimento da hipotenusa AB do triângulo retângulo AOB, mede raiz de 2:
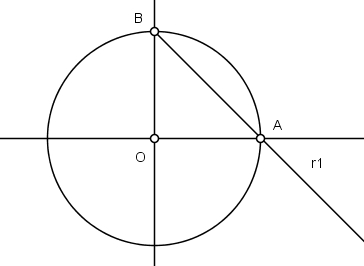
2) Trace a semirreta r2 ortogonal à r1 em B:
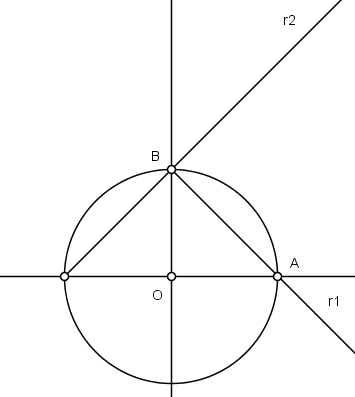
3) Com centro em B descreva uma circunferência de raio r = OB = 1 e marque o ponto C em r2. O triângulo retângulo ABC tem hipotenusa AC igual a raiz de 3:
4) Com centro em A, descreva uma circunferência de raio AC e marque como D a intersecção com r1. O segmento BD aproxima π a um valor de 3,1462...
Vamos ver, agora, algebricamente:
Sendo o raio AO = 1, temos que a hipotenusa AB do triângulo retângulo AOB mede:
Por construção, o segmento BC mede 1 e a hipotenusa AC do triângulo retângulo ABC mede:
Assim, o segmento BD aproxima π em duas casas decimais:
Veja mais:
Construindo Raízes de Números Naturais
Retificação da Circunferência (Parte 1) (Parte 2) (Parte 3) (Parte 4)
Como Construir uma Aproximação para a Quadratura do Círculo com Régua e Compasso

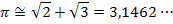


Primeira vez que vejo esta aproximação. Só lembrava da raíz de dez.
ResponderExcluirShow de bola.
ResponderExcluirvou questionar meu professor de matematica para ver o que ele me diz sobre isso!
valeu amigão.
Olá amigo. Por mais que estudemos a Matemática, sempre terá assuntos que não dominamos. A Matemática é muito ampla e somente grandes gênios tem domínio absoluto. uma construção como esta é relativamente simples, mas não é difundida em livros e talvez poucas pessoas saibam como construir esta aproximação.
ExcluirAbraços.