No primeiro artigo sobre Integração por Frações Parciais, vimos a técnica para integrar quando o integrante é uma fração racional e o denominador é um fator linear. Vamos ver agora como proceder se o denominador da fração racional do integrante é um fator quadrático irredutível.
Caso 3 – Fatores Distintos do Segundo Grau
A cada fator do segundo grau irredutível da forma ax2 +bx + c que aparece uma vez no denominador de uma fração raciona própria, corresponde a uma fração parcial da forma:
onde A e B são constantes a determinar.
Exemplo 1: Achar a integral:
a) Primeiramente, fatoramos o denominador:
Fazemos:
Temos então que:
ou
b) Agora, vamos determinar as constantes. Observando em (3) os coeficientes das potências semelhantes de x em ambos os membros da igualdade, podemos montar um sistema de equações:
Resolvendo o sistema, obtemos: A1 = 1, A2 = 0 e A3 = –1.
c) Agora, vamos reescrever a integral como:
Completando quadrado, para o denominador do integrando, temos que:
Assim:
Fazemos integração por substituição. Seja:
Então:
A integral:
Desta forma, temos que:
Caso 4 – Fatores Repetidos do Segundo Grau
A cada fator do segundo grau irredutível da forma ax2 +bx + c que aparece n vezes no denominador de uma fração racional própria, corresponde a uma soma de n frações parciais da forma:
onde A1, A2, ..., An e B1, B2, ..., Bn são constantes a determinar.
Exemplo 2: Achar a integral:
a) Primeiramente, fatoramos o denominador. Vejam que o fator que se repete é o (x2 + 2x + 3). Como aparece duas vezes, fazemos:
Temos então que:
ou
b) Agora, vamos determinar as constantes. Observando em (3) os coeficientes das potências semelhantes de x em ambos os membros da igualdade, podemos montar um sistema de equações:
Resolvendo o sistema, obtemos: A1 = 0, A2 = 1, A3 = –1 e A4 = –1.
c) Agora, vamos reescrever a integral como:
Para a primeira integral, completamos quadrado e para resolver as duas integrais, aplicamos o método de integração por substituição, encontrando:
Referências:
[1] Cálculo Diferencial e Integral – Frank Ayres Jr – Coleção Schaum



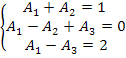
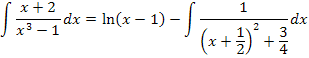
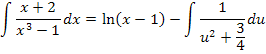
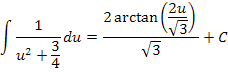
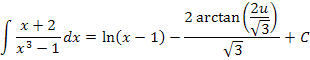
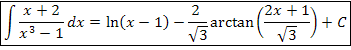
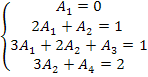
![clip_image002[4] clip_image002[4]](http://lh3.ggpht.com/-fvKR2gDLxcc/T9R_EItOUaI/AAAAAAAATdk/9Mq2XwVQoBM/clip_image0024_thumb%25255B2%25255D.gif?imgmax=800)

O desenvolvimento em frações parciais é uma técnica muito útil tanto em Cálculo como em transformadas de Laplace. Recentemente vi que o caminho natural para calcular a transformada discreta inversa de Laplace é o desenvolvimento em frações parciais. Este post é uma contribuição a todos nós. Parabéns!
ResponderExcluirQuando eu estava pesquisando sobre este tema, vi que também se relacionava com a transformada de Lapalace, mas não saberia como escrever um artigo sobre. Acho que isso é para você mesmo.
ResponderExcluirEsse método não aprendi na minha graduação. Na verdade, tenho visto muitas coisas que não aprendi na graduação. Por um lado é bom que vou aprendendo cada vez um pouco mais; mas por outro é muito triste, porque vejo que não aprendi quase nada. Acho que a instituição prefere manter um currículo básico para manter alunos e não desestimulá-los e assim não perder a renda mensal. Esse é um dos problemas de faculdades privadas.
Um abraço Paulo!
Olá, também fico triste com isso. Em cálculo 1 não vi capítulos importantes como: máximos e mínimos, e taxas. Faço eng. de petróleo e vejo que nos concursos da Petrobras cai muitos destes tópicos. Em cálculo 2, o professor era ótimo, mas a turma bem limitada e com isso ele tinha que ensinar bem devagar, ainda assim conseguimos chegar em volumes. Isso entristece realmente. Grande abraço.
ExcluirEntendo o que diz. Minha turma também tinha mmuitas pessoas limitadas, o que prejudicou o desenvolvimento dos demais. Tive ótimos professores, mas devido a esse contexto, tiveram que adaptar suas formas de ensino. Quem perdeu fomos nós que realemnte queríamos aprender.
ExcluirAbraços.
Realmente o método de ensino na graduação no Brasil é medonho...só serve para espantar os alunos das exatas (enche de exercícios e provas) como se isso fosse a solução para que os profissionais de exatas resolvessem todos os desafios da carreira de engenharia. Sempre estudo muito e agora tenho mais facilidade depois de começar o curso do prfessor Ricieri.
ResponderExcluirAbraços
Wagner
Bom dia, professor, eu postei na outra página, mas era para postar aqui. No seu exemplo do caso das integrais com fatores repetidos de grau 2, eu não entendi como se integraria se o numerador não fosse x+1 mas, por exemplo, 1.
ResponderExcluirUm exemplo mais fácil do que eu quero dizer:
$$ \displaystyle \int 1/(1+x^2)^2 dx $$
Bom dia. Deve-se usar substituição trigonométrica. Veja resolução no link abaixo:
Excluirhttp://obaricentrodamente.blogspot.com.br/2013/04/integral-de-11x22dx.html
Para o caso geral, veja no final da resolução o link para Integral por substituição trigonométrica.
Um abraço!
Sou estudante de engenharia civil e recentemente eu me deparei com uma integral que até agora ninguém conseguiu resolver. Nem mesmo os meus professores de cálculo chegaram à conclusão.
ResponderExcluirAlguém de vocês poderiam ajudar?
∫x²e^(x²)dx
Olá Luan,
ResponderExcluirEstou vendo como resolvê-la, mas por enquanto, veja a solução dada pela Wolfram:
http://www.wolframalpha.com/input/?i=int+x^2e^%28x^2%29dx
Abraços.
Luan,
ResponderExcluirVeja a resolução desta integral no link:
http://obaricentrodamente.blogspot.com.br/2013/04/a-funcao-erro-e-outras-funcoes.html
Um abraço.
agradeço foi muita útil para mim.
ResponderExcluirEste site foi de grande ajuda, obrigado.
ResponderExcluirOlá, tudo bem ?
ResponderExcluirExiste um erro no exemplo 1, a integral é x+2 e não x²+2 como o senhor fez! Obrigado.
È, também observei isto.
ExcluirTambém observei isso. Na verdade, preferi alterar o enunciado, já que a solução foi feita considerando x²+1.
ResponderExcluir