Se desejarmos multiplicar duas frações, hoje fazemos automaticamente, multiplicando os numeradores e os denominadores:
Para ilustrar esse conceito de multiplicação, vamos usar círculos para podermos visualizar todo o procedimento.
Seja a multiplicação entre duas frações:
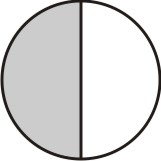
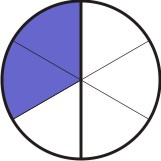
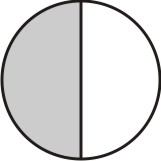
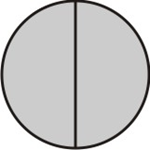
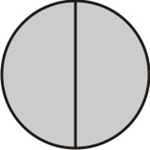
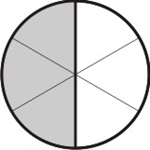
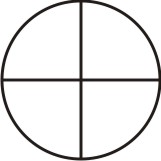
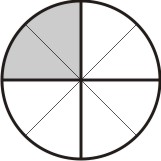
Começamos tomando uma das frações; pode ser 1/2 ou 2/3. Vamos tomar a fração 1/2 como referência. Dividimos um círculo em partes iguais ao denominador desta fração, que no caso é dois, e hachuramos partes iguais ao seu numerador, no caso 1:
[Figura 1]
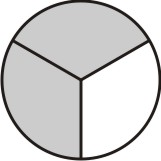
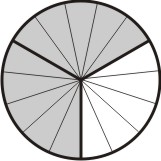
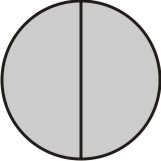
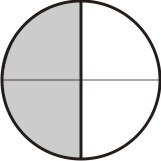
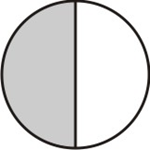
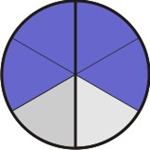
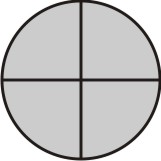
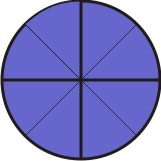
Agora, subdividimos cada uma dessas partes em partes menores em quantidades iguais ao denominador da segunda fração, que neste caso é 3:
[Figura 2]
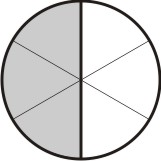
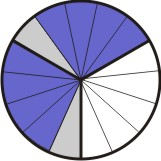
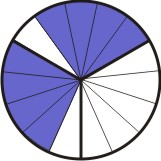
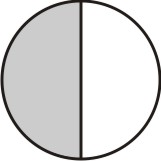
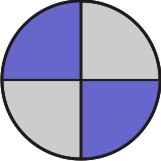
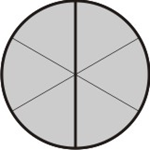
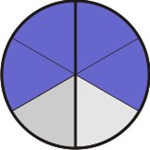
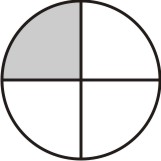
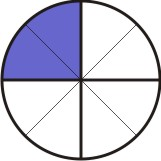
Agora, para cada parte hachurada, tomamos a quantidade de subdivisões iguais ao numerador da segunda fração, que no caso é 2:
[Figura 3]
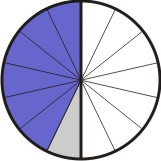
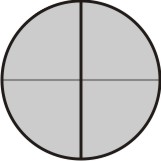
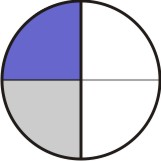
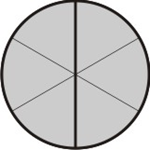
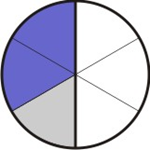
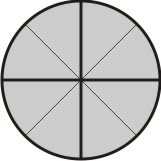
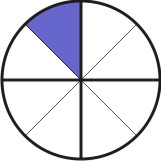
Desta forma, o círculo original foi dividido em 2 partes e depois cada parte subdividida em três, totalizando 6 subdivisões, tomamos duas delas, ou seja: 2/6:
[Figura 4]
Que vale o produto:
Desta forma, se quisermos uma multiplicação entre duas frações, seguimos os passos:
a) Tomamos uma das frações;
b) Dividimos um círculo em partes iguais ao seu denominador;
c) Hachuramos partes iguais ao seu numerador;
d) Subdividimos cada uma dessas partes em “partes menores” iguais ao denominador da segunda fração;
e) Tomamos, para cada parte hachurada, a quantidade de subdivisões iguais ao numerador da segunda fração.
Em relação a frações, podemos ter frações próprias e frações impróprias.
Definição 1: Fração própria é aquela onde o numerador é menor que seu denominador:
Exemplos:
Definição 2: Fração imprópria é aquela onde o numerador é maior que seu denominador:
Exemplos:
Desta forma, no caso da multiplicação entre duas frações, podemos ter três casos distintos:
Caso 1: As duas frações são próprias:
Caso 2: Uma fração é própria e a outra imprópria:
Caso 3: As duas frações são impróprias:
Vamos exemplificar agora, cada um dos três casos e ver as diferenças em cada procedimento.
Exemplo 1: Seja multiplicar as frações:
As duas frações são próprias. Vamos tomar como referência a fração 2/3. Assim, dividimos um círculo em três partes e hachuramos duas delas:
[Figura 5]
Subdividimos cada parte em cinco partes iguais:
[Figura 6]
Tomamos a quantidade de 4 subdivisões para cada parte hachurada:
[Figura 7]
O produto desejado é a quantidade de subdivisões selecionadas, dividida pela quantidade de subdivisões totais, ou seja, temos 8 subdivisões selecionadas de 15 totais. Assim:
[Figura 8]
Que vale o produto:
Exemplo 2: Seja multiplicar as frações:
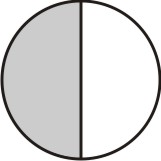
As duas frações são próprias. Utilizamos o mesmo procedimento. Primeiramente tomamos uma das frações como referência. Vamos tomar a fração 1/2. Assim, dividimos um círculo em duas partes e hachuramos uma delas:
[Figura 9]
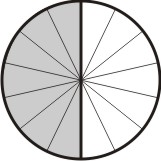
Subdividimos cada metade em partes iguais ao denominador da outra fração, que no caso é oito:
[Figura 10]
Tomamos sete partes das oito subdivisões:
[Figura 11]
Que vale o produto:
Exemplo 3: Seja multiplicar as frações:
Neste exemplo, temos a multiplicação entre uma fração própria e uma imprópria. Nestes casos, tomamos como referência a fração imprópria, pois fica mais fácil a visualização. Utilizamos, então, a fração 3/2. Dividimos um círculo em duas partes iguais e hachuramos três:
[Figura 12]
Ops! Se temos duas partes e precisamos hachurar três, faltará uma; então, adicionamos mais um círculo dividido em duas partes:
[Figura 13]
Subdividimos cada uma dessas três partes hachuradas em dois, que é o denominador da segunda fração:
[Figura 14]
Agora, tomamos uma subdivisão de cada parte:
[Figura 15]
Que vale o produto:
Exemplo 4: Seja multiplicar as frações:
Esta é uma multiplicação entre uma fração própria e uma imprópria. Tomamos a fração 5/2 como referência. Então, dividimos os círculo em duas partes iguais:
[Figura 16]
Subdividimos cada parte em três, que é o denominador da segunda fração:
[Figura 17]
Tomamos duas subdivisões de cada parte hachurada:
[Figura 18]
Que vale o produto:
Exemplo 5: Seja multiplicar as frações:
Neste caso, temos a multiplicação entre duas frações impróprias. Vamos tomar a fração 5/4 como referência. Assim, dividimos cada círculo em quatro partes iguais:
[Figura 19]
Devemos hachurar cinco partes, mas como o círculo só possui quatro partes adicionamos mais círculos, quantos forem necessários:
[Figura 20]
Agora, devemos subdividir cada parte em duas, conforme indica o denominador da fração 3/2:
[Figura 21]
Temos de tomar três subdivisões de cada parte, conforme indica o numerador da fração 3/2, mas cada parte só possui duas subdivisões. Então, adicionamos quantos círculos forem necessários:
[Figura 22]
Temos então que cada círculo foi subdividido em 8 partes; e temos 15 subdivisões selecionadas. Logo, o produto desejado é:
Exercícios para casa: Efetue as multiplicações utilizando o conceito geométrico:
Veja mais:
Trabalhando com Frações
O Método da Gelosia para Multiplicações
Método da Multiplicação dos Camponeses Russos
Um Método para a Multiplicação Entre Dois Números

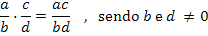



Postar um comentário