O algoritmo de Euclides é um dos algoritmos mais antigos conhecidos e o método destaca-se por ser simples e eficiente para a determinação do $mdc$ entre números inteiros diferentes de zero.
O método aparece pela primeira vez no Livro VII de sua obra Os Elementos, cerca de 300 a. C. e tem sua origem geométrica, como a determinação da maior medida comum entre dois segmentos de reta.
Proposição II do Livro VII:
Sendo dados dois números não primos entre si, achar a maior medida comum deles.
Esta proposição nos diz que dados os segmentos $AB$ e $CD$ representando dois números não primos entre si e diferentes de zero, existe um terceiro segmento $EF$ que cabe um número inteiro de vezes nos primeiros dois segmentos, ou seja, o segmento $EF$ mensura os segmentos $AB$ e $CD$.
Para uma demonstração mais moderna, vamos considerar o lema abaixo:
Lema 1:
Sejam $a$, $b$ e $m$ inteiros. Temos que:$$mdc(a, 0) = |a|
$$
e que:
$$
mdc(a,b) = mdc(b,a) = mdc(|a|, |b|) = mdc(a - mb, b)
$$
Para calcular o $mdc(a, b)$, tendo em vista o lema acima, vamos supor que $a$ e $b$ são não negativos. Se $b = 0$ ou $a = b$, então $mdc(a,b) = a$ e nada temos que calcular. Vamos supor que $a \neq b$, como $mdc(a, b) = mdc(b, a)$, podemos supor que $a > b > 0$.
Pela divisão euclidiana, temos que:
a=b \cdot q_1 + r_2
$$
onde $0 \leq r_2 < b$.
Da igualdade acima e pelo Lema 1, temos que:
$$mdc(a,b) = mdc(a-b\cdot q_1, b) = mdc(r_2,b)=mdc(b,r_2)
$$
Desta forma, podemos ter duas situações:
$a_1)$ $r_2=0$. Neste caso, temos:
$$mdc(a, b) = mdc(b, r2) = mdc(b, r2) = b
$$
$b_1)$ $r_2 \neq 0$. Neste caso, efetuamos a divisão euclidiana de $b$ por $r$, obtendo:
$$b = r_2 \cdot q_2 + r_3
$$
onde $0\leq r_3 <r_2
$$
Segue que:
$$mdc(a,b) = mdc(b,r_2) = mdc(r_2,r_3)
$$
Novamente, duas novas situações podem ocorrer:
$a_2)$ $r_3=0$. Neste caso, temos:
$$(a, b) = (r_2, 0) = r_2
$$
$b_2)$ $r_3 \neq0$. Neste caso, efetuamos a divisão euclidiana de $r_2$ por $r_3$, obtendo:
$$r_2 = r_3 \cdot q_ 3+r_4
$$
onde $0 \leq r_4 < r_3$.
Segue que:
$$mdc(a,b) = mdc(b,r_2) = mdc(r_2,r_3) = mdc(r_3,r_4)
$$
e assim sucessivamente.
Definido $r_1=b$, existe um valor $n$ tal que $r_{n+1} = 0$ e $r_n \neq 0$. De fato, se tivéssemos para todo $n\neq 0$, teríamos uma sequência infinita $r_1,r_2,r_3,\cdots$, tal que:
$$r_1 > r_2 > r_3> \cdots > 0
$$
Segue que:
$$mdc(a,b)=mdc(b,r_2)=\cdots = mdc(r_n,r_{n+1}) = mdc(r_n,0)=r_n
$$
Portanto, o último resto não nulo $r_n$ deste processo, fornece o valor de $mdc(a.b)$.
Calculamos o $mdc(a, b)$ através do dispositivo prático que decorre do processo acima, que chamamos de Algoritmo de Euclides.
Exemplo 1:
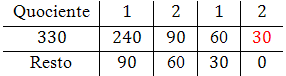
Calcular o $mdc(330, 240)$. Neste caso, $a = 330$ e $b = 240$.
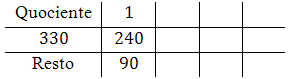
Dividimos $a$ por $b$:
Assim, temos que $q_1=1$ e $r_1=90$. Inserimos estes valores na grade:
Agora, dividimos $240$ por $90$:
Assim, temos que $q_2=2$ e $r_2=60$. Inserimos estes valores na grade:
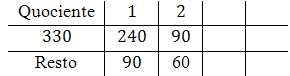 Agora, dividimos $90$ por $60$:
Agora, dividimos $90$ por $60$:
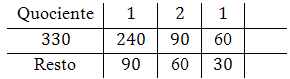
Assim, temos que $q_3=1$ e $r_3=30$. Inserimos estes valores na grade:
Agora, dividimos $60$ por $30$:
Assim, temos que $q_4=2$ e $r_4=0$. Inserimos estes valores na grade:
Como obtivemos um resto igual a zero, o $mdc$ procurado é o último $r_n$ não nulo:
$$mdc(330,240) = 30
$$
Exemplo 2:
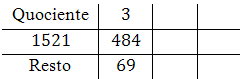
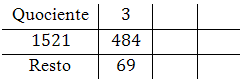
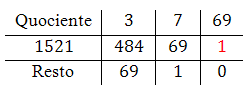
Calcular o $mdc(484,1521)$. Neste caso, fazemos $a = 1521$ e $b = 484$.
Dividimos $a$ por $b$:
Assim, temos que $q_1=3$ e $r_1=69$. Inserimos estes valores na grade:
Agora, dividimos $484$ por $69$:
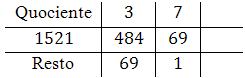
Assim, temos que $q_2=7$ e $r_2=1$. Inserimos estes valores na grade:
Agora, dividimos $69$ por $1$:
Assim, temos que $q_3=69$ e $r_3=0$. Inserimos estes valores na grade:
Como obtivemos um resto igual a zero, o $mdc$ procurado é o último $r_n$ não nulo:
$$mdc(484,1521)=1
$$
Exemplo 3:
Calcular o $mdc(4074, 582)$. Neste caso, $a = 4086$ e $b = 582$.
Dividimos $a$ por $b$:
Assim, temos que $q_1=7$ e $r_1=12$. Inserimos estes valores na grade:
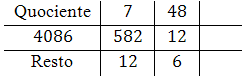
Agora, dividimos $582$ por $12$:
Assim, temos que $q_2 = 48$ e $r_2 = 6$. Inserimos estes valores na grade:
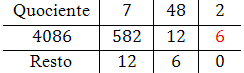
Agora, dividimos $12$ por $6$:
Assim, temos que $q_3 = 2$ e $r_3 = 0$. Inserimos estes valores na grade:
Como obtivemos um resto igual a zero, o $mdc$ procurado é o último $r_n$ não nulo:
$$mdc(4086, 582)=6
$$
Referências:
- Curso de Álgebra V1 – Abramo Hefez – IMPA
- Os Elementos de Euclides – Tradução e Irineu Bicudo






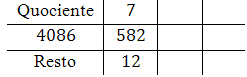

e demais esse site, eu não me dei bem na prova e vou estudar mais nessa vez..........
ResponderExcluiramei me ajudou muito sz
ResponderExcluirApenas uma pequena gralha:
ResponderExcluirExemplo 3: Calcular o mdc(4074, 582). Neste caso, a = 4086 e b = 582.
Pede para calcular com 4074 e depois resolve com 4086.
Tudo o resto está muito bem explicado. Parabéns.
Olá Prinfor.
ExcluirRealmente um deslize. Em breve farei a correção.
Um abraço.
faça o uso do algoritmo de euclides e encontre o mdc de 50,90,300. me ajuda..
ResponderExcluirO algoritmo de Euclides funciona com números negativos?
ResponderExcluir