Ernest Willian Hobson, nasceu a 27 de outubro de 1856 em Derby, Inglaterra e morreu em 19 de abril de 1933 em Cambridge.
Foi educado em ambiente rigidamente religioso e parece ter sentido os grilhões dogmáticos pesarem e resolveu afastá-los, desenvolvendo fortes convicções do racionalismo, tornando-se um reconhecido radical e agnóstico.
Ele não foi um prodígio em matemática; frequentou a escola de Derby, sendo bem educado, mas não conseguiu brilhar. Estudou no Royal College os Science e ganhou uma bolsa que lhe permitiu estudar física com Frederick Guthrie na Royal School os Mines. Em seguida ganhou uma bolsa de matemática do Christ’s College, em Cambridge, entrando em 1874. Graduou-se em 1878 sendo considerado mais notável como um pensador do que uma calculadora. Lecionou na Universidade de Cambridge até o fim de sua vida.
Ainda jovem foi apresentado à análise moderna e fez contribuições reais à matemática. Concentrou seus esforços, em particular, a convergência de séries de funções ortogonais.
Hobson publicou seu trabalho A Treatise on Trigonometry em 1891 e em 1907 publicou seu livro Theory os Functions os a Real Variable. Outro livro publicado por Hobson foi Squaring the Circle em 1913, onde aborda as principais passagens da história do problema da quadratura do círculo.
Hobson construiu geometricamente um segmento de reta de comprimento 1,77247, que se aproxima à raiz quadrada de π a partir de um círculo de raio unitário. Desta forma, se um quadrado for construído com lado aproximadamente igual à raiz de π, sua área será aproximadamente igual a π, que é a área do círculo de raio unitário.
Construção:
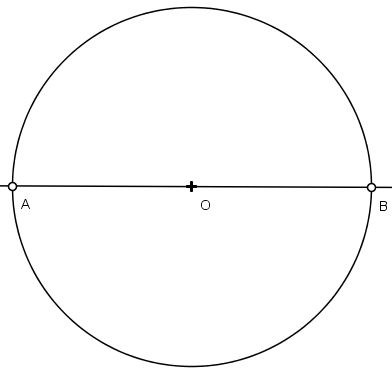
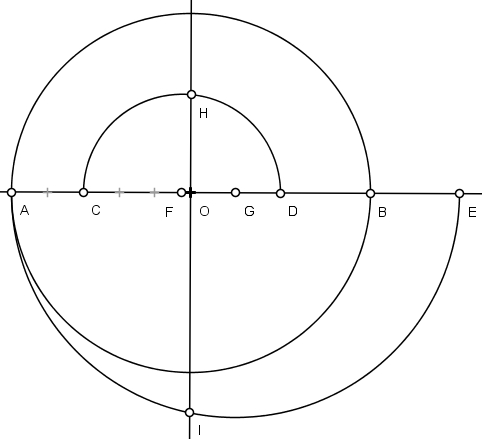
1) Descreva uma circunferência de raio unitário com centro em O e diâmetro AOB:
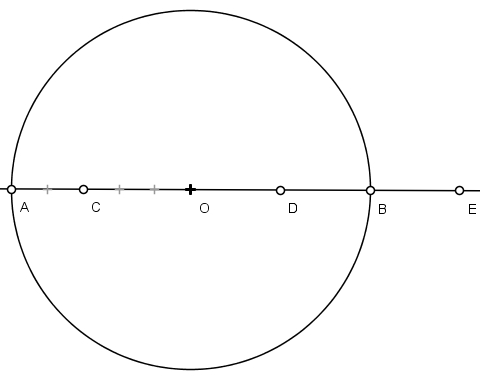
2) Marque o ponto C igual a 3/5 do raio; o ponto D igual a 1/2 raio e o ponto E a 3/2 do raio:
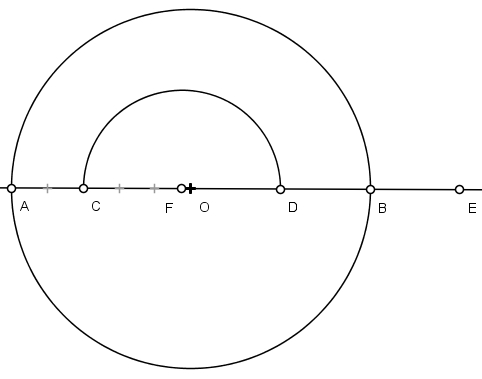
3) Descreva o arco de diâmetro CFD com centro em F:
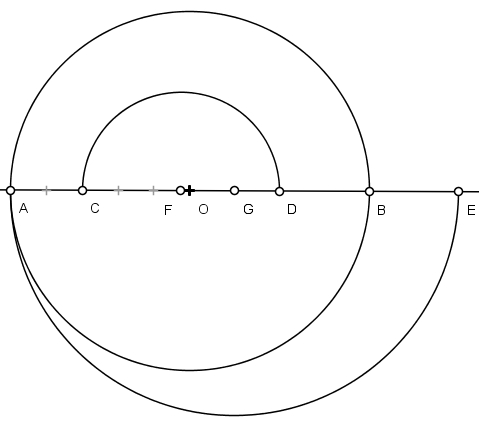
4) Descreva o arco de diâmetro AGE com centro em G.
5) Trace a perpendicular AOB por O e marque os pontos H e I com as intersecções com os arcos CFD e AGE:
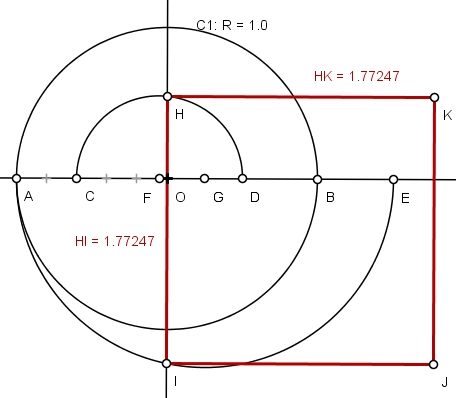
6) O segmento HI aproxima a raiz quadrada de π em 1,77246742...:
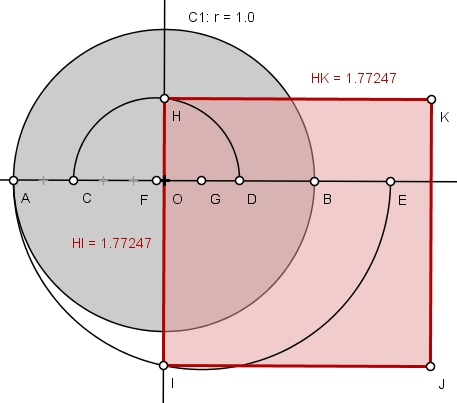
Desta forma, se construirmos um quadrado de lado HI, encontraremos um uma área muito próxima à do círculo C1 de raio unitário:
Prova:
Sejam:
O diâmetro CD será dado por:
E assim:
O segmento OF será dado por:
Do triângulo FOH, reto em O, aplicamos o teorema pitagórico:
O segmento FH é o raio do arco CFD igual ao segmento FC:
Da mesma forma, temos que:
Temos que o segmento OG é dado por:
Do triângulo GOI, temos que:
Desta forma, temos que o segmento desejado é dado pela soma:
Então, se construirmos um quadrado de lado HI, este terá uma área muito próxima da área do círculo de raio unitário:
Vemos que o erro é da ordem de 4 x 10 –5 unidades de área.
Referências:
[1] Squaring the Circle – A History of the Problem – Hernest W. Hobson – 1913
Veja mais:
Como Construir uma Aproximação para a Quadratura do Cìrculo com Régua e Compasso
Retificação da Circunferência (Parte 1) (Parte 2) (Parte 3) (Parte 4) (Parte 5)
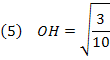
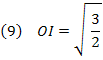
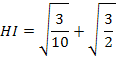
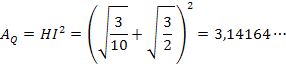
A visita a este site está a ser um "passeio" fenomenal! Os meus parabéns e os meus reconhecidos agradecimentos!
ResponderExcluirSempre fui um aficionado da Matemática. Pena tenho, e muita, que os percalços da vida não me tenham permitido ir tão além quanto gostaria.
Não sei se este será o local próprio para contar uma história antiga e pedir uma ajuda...
Um dia, em 1965, 4 jovens, num jantar de despedida para ingresso no serviço militar, são abordados por um sujeito de um outro grupo de 4 adultos, de uma mesa próxima que haviam acompanhado as nossas conversas sobre a ida para "a guerra"... Eles eram militares, oficiais supomos...
Então ele propôs-nos que, se resolvêssemos um problema matemático, ele e os 3 amigos pagariam a nossa conta.
Dá para entender a motivação para o trabalho, não é verdade?
Pois bem, não conseguimos e ainda hoje, 50 anos depois, não sei a solução.
E o problema é tão simples, pelo menos na sua descrição!...
Tomemos um quadrado com lado = 10. Fazendo centro em cada um dos vértices, obtém-se uma área inscrita no quadrado pela intersecção dos 4 quartos de círculo. E a pergunta é: Qual a área da área inscrita?
Será que dá para demonstrar como se obtém a solução?
Muito grato!
Armando Graça (Lisboa, Portugal)
Prezado Armando, obrigado pelo prestígio. Este blog é aberto a todos que queiram participar, fique à vontade.
ExcluirVou pensar numa solução para o seu problema.
Um abraço e volte sempre.