Como Desenhar um Ovo de Galinha com Régua e Compasso (Parte 1)

Este é o primeiro post de uma série que pretendo publicar aqui no blog sobre a construção geométrica do ovo de galinha. Não são aproximações, são curvas reais dos ovos.

Robert Dixon, em seu livro Mathographics, de 1987, denomina essas curvas ovoides de Ovos Euclideanos, cujo termo tem explicação simples: tem mais a ver com a Ciência Matemática do que com propriamente com pássaros.

As construções baseiam-se em traçados de circunferências, onde arcos de diferentes raios se unem dando a continuidade na curva. Para que haja essa continuidade, há uma técnica simples que vamos aprender rapidamente para prosseguirmos com as construções.

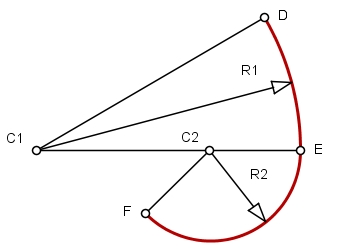
Primeiro caso – as concavidades dos arcos estão voltadas para um mesmo lado: Num segmento de reta C₁E, descreva o arco DE com centro em C­₁ e raio R₁ = C₁E. Com centro em C_2, localizado em qualquer ponto da reta C₁E, e raio R₂ = C₂E, descreva o arco EF. Vejam que o ponto E é onde ocorre a mudança de raio da curva DEF, mantendo sua continuidade.

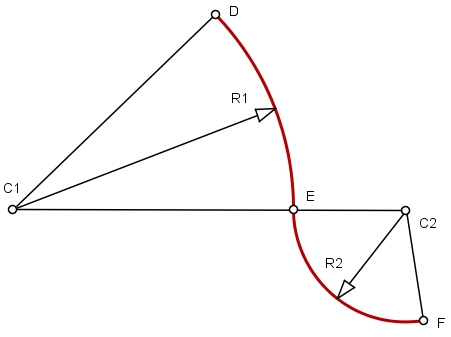
Segundo caso – as concavidades dos arcos estão voltadas para lados opostos: Num segmento de reta C₁C₂, descreva o arco DE com centro em C₁ e raio R₁ = C₁E, menor que o segmento de reta dado. Com centro em C₂ e raio R₂ = C₂E, descreva o arco EF. Vejam que o ponto E é o ponto de inflexão, ou seja, onde a curva muda a concavidade, sem perder a continuidade.

Assimilando esses conceitos básicos, já podemos iniciar a construção efetiva do ovo.

Construção

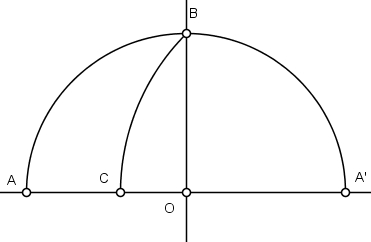
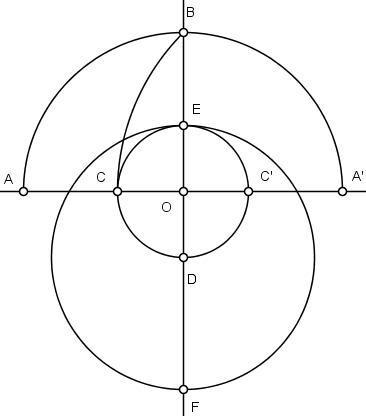
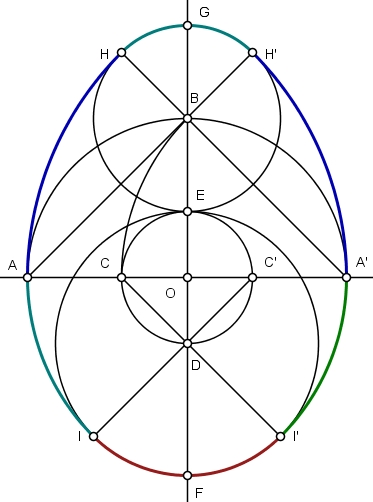
Inicie a construção num eixo ortogonal descrevendo um arco superior centrado na origem marcando os pontos A, A’ e B.

Com raio igual a A’B, descreva um arco marcando como C a intersecção com o eixo horizontal.

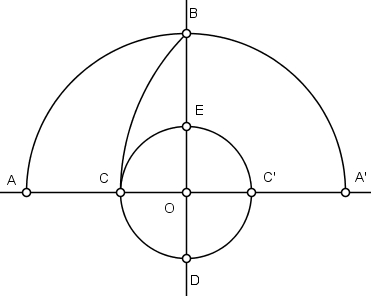
Com raio igual a OC e centro na origem, descreva uma circunferência, marcando os pontos C’, D e E.

Com centro em D e raio DE, descreva uma circunferência marcando o ponto F.

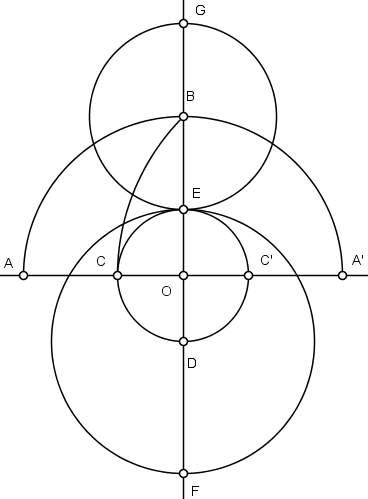
Com centro em B e raio BE, descreva uma circunferência marcando o ponto G.

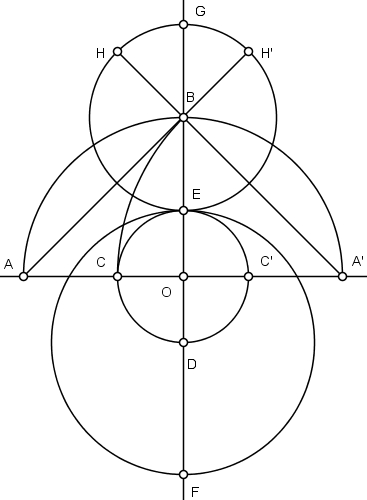
Trace um segmento de reta que inicia em A, passe por B e marque como H’ a intersecção com a circunferência de centro em B. Proceda da mesma forma para o segmento que inicia em A’ e passa por B, gerando o ponto H.

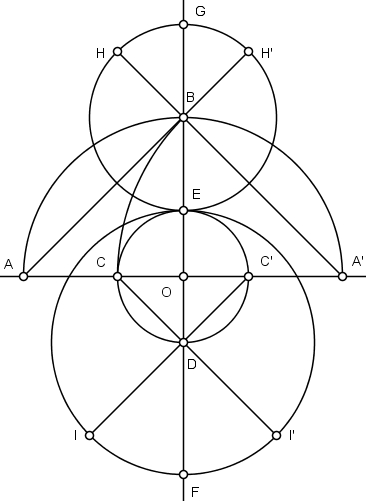
Trace um segmento de reta que inicia em C, passa por D e intercepta a circunferência de centro em D no ponto I’. Proceda da mesma forma para o segmento que inicia em C’ e passa por D, gerando o ponto I.

 

Todos os pontos já foram definidos. Basta agora unirmos os arcos de modo contínuo, lançando mão dos dois casos discutidos no início deste post.

Com centro em D, descreva o arco FI’, em vermelho;

Com centro em C, descreva o arco I’A’, em verde;

Com centro em A, descreva o arco A’H’, em azul;

Com centro em B, descreva o arco H’G, em turquesa;

Proceda analogamente para o hemisfério esquerdo da construção.

Referências:

[1] Mathographics – Robert Dixon

---

Veja mais:

Como Desenhar um Ovo de Galinha com Régua e Compasso (Parte 1)
Construções Geométrica do PHI
Retificação da Circunferência

---