O método Tabular para resolver integrais por partes

Para certos tipos de integrais, utilizamos o método de integração por partes, geralmente quando há um produto entre funções, como por exemplo um polinômio e uma função trigonométrica:

$$
\int x\cdot \cos(x) \ dx
$$

Nestes casos, pensamos no integrando como um produto $u \cdot dv$, onde a parte chamada $dv$ deve ser algo que possa ser integrada e a parte chamada $u$ deve ser algo que possa ser simplificado por derivação. Basicamente, temos:

$$
\int u\ dv = uv - \int v\ du
$$

🔗 Veja este estudo específico sobre o método de integração por partes

O método Tabular, em muitos casos, pode levar ao resultado bem mais rápido, se comparado ao método tradicional por partes, muito embora, tenha particularidades e nem sempre seja a melhor opção. O que definirá seu uso é a prática.

Este método dispõe as informações em uma tabela contendo uma coluna para $u$ e suas derivadas, outra para $dv$ e suas integrais e outra para os sinais de $+$ ou $-$.

Dadas duas funções $f(x)$ e $g(x)$, definidas em um intervalo aberto $I$, onde $f = f^{(0)}, f^{(1)}, f^{(2)}, \cdots , f^{(n)}$ denota as $n$ derivadas de $f$ e $g = g^{(0)}, g^{(-1)}, g^{(-2)}, \cdots , g^{(-n)}$ denotas as $n$ antiderivadas de $g$.

Em uma coluna listamos $f$ e suas $n$ derivadas e em uma coluna adjacente listamos $g$ e suas $n$ integrais. Usaremos $u$ e $dv$, respectivamente, no cabeçalho das colunas de acordo com a notação padrão usada no método de integração por partes.

Em seguida, multiplicamos diagonalmente para baixo, da coluna $u$ para $dv$, adicionando e subtraindo cada um desses produtos de forma alternada, como indicado na figura abaixo:

Podemos escrever a integral:$\displaystyle I = \int f(x)\ g(x)\ dx$ através do somatório:

$$
I = \color{blue}{\sum_{i=0}^{n-1}} \color{red}{(-1)^i} \color{blue}{f^{(i)}(x) \cdot g^{(-(i+1))}(x)} + \color{red}{(-1)^n} \color{green}{\int f^{(n)}(x) \cdots g^{(-n)}(x)\ dx}
$$

A parte em azul da relação acima, representa a soma de todos os produtos entre $u$ e suas derivadas com $dv$ e suas integrais, realizadas diagonalmente para baixo. O sinal entre as parcelas é definido pelo $(-1)^i$, que na prática, fica alternando entre $+$ e $-$. A parte em verde, representa a integral do produto da última linha.

Os produtos que compões o integrando da função original podem ser entre funções polinomiais, logarítmicas, trigonométricas, inversas e exponenciais.

Mas, como sabemos quando parar com as derivadas de $u$ e as integrais de $dv$? Isso vai depender se uma das funções envolvidas é uma função polinomial.

Vamos dividir as resoluções em dois grupos: de integrais em que uma das funções é um polinômio e de funções que não sejam polinômios.

Integrais onde uma das funções é um polinômio

Uma função polinomial envolve um ou mais termos do tipo: $\alpha x^n$.

Podemos ter um produto entre uma função polinomial com outras:

$$
[\text{ Polinomial }] \times \
\begin{cases}
[\text{ Logarítmica }]\\
[\text{ Exponencial }]\\
[\text{ Trigonométrica }]\\
[\text{ Inversas }]
\end{cases}
$$

Neste caso, colocamos $u$ como sendo a função polinomial e vamos diferenciando até encontrarmos uma derivada igual a $0$ (zero).

Para um polinômio de graus $n$, precisaremos fazer $n+1$ diferenciações para encontrarmos uma derivada igual a $0$.

No entanto,, nem sempre o polinômio deverá estar listado na coluna $u$. Devemos sempre analisar o produto e ver qual das funções é mais facilmente simplificada por derivação. Um exemplo é quando uma das funções é o $\ln(x)$. Veremos mais adiante alguns exemplos.

Exemplo 1:

Calcular a integral $I = \displaystyle \int x \ \text{sen}(x)\ dx$.

Na coluna $u$ colocamos $x$ e suas derivadas e na coluna $dv$ colocamos $\text{sen}(x)$ e suas integrais. Na coluna do sinal, iniciamos com o sinal $+$ e vamos alternando entre $+$ e $-$. Como o grau do polinômio é um $(x)$, precisamos efetuar duas derivações.

Como o grau do polinômio $(x)$ é igual a $1$, precisamos efetuar duas derivações.

Vamos colocar o polinômio $x$ na coluna $u$ e a função trigonométrica $\text{sen}(x)$ na coluna $dv$:

A solução será:

$$
I = \color{red}{+} \color{blue}{x \left( - \cos(x) \right)} \color{red}{-} \color{blue}{1\left( - \text{sen}(x) \right)} \color{red}{+} \color{green}{\int 0 \cdot \left(-\text{sen}(x) \right) dx} $$

$$
I = -x\ \cos(x) + \text{sen}(x) + C\\
\ \\
I = \text{sen}(x) - x\ \cos(x) + C
$$

Vejam que a última linha representa $\displaystyle \int 0 \cdot \left(-\text{sen}(x)\right)\ dx$, que é uma constante. Então, efetivamente não precisamos incluir no cálculo.

Exemplo 2:

Calcular a integral $\displaystyle I = \int x^2\ \cos(x)\ dx$.

Como o grau do polinômio $(x^2)$ é igual a $2$, devemos efetuar três derivações.

Vamos colocar o polinômio $x^2$ na coluna $u$ e a função trigonométrica $\cos(x)$ na coluna $dv$:

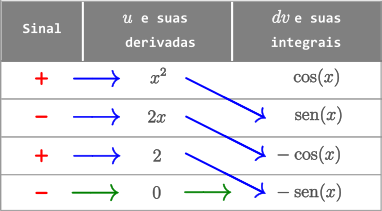
A solução será:

$$
I = \color{red}{+} \color{blue}{x^2 \text{sen}(x)} \color{red}{-} \color{blue}{2x \left(-\cos(x)\right)} \color{red}{+} \color{blue}{2\left(-\text{sen}(x)\right)} + C $$

$$
I = x^2 \text{sen}(x) + 2x \cos(x) - 2\ \text{sen}(x)+C
$$

Exemplo 3:

Calcular a integral $\displaystyle I = \int 3x^2 \ e^{2x}\ dx$.

Como o grau do polinômio $(3x^2)$ é igual a $2$, devemos efetuar três derivações.

Poderíamos neste caso listar $e^{2x}$ e suas derivadas na coluna $u$, mas vamos o exponencial na coluna $dv$. Lembrando que a integral de $e^{ax}$ é $\displaystyle \frac{e^{ax}}{a}$.

A solução será:

$$
I = \color{red}{+} \color{blue}{3x^2 \cdot \frac{1}{2}e^{2x}} \color{red}{-} \color{blue}{6x \cdot \frac{1}{4}\ e^{2x}} \color{red}{+} \color{blue}{6\cdot \frac{1}{8}e^{2x}} + C $$

$$
I = \frac{3}{2} x^2 e^{2x} - \frac{3}{2} x\ e^{2x} + \frac{3}{4} e^{2x} + C\\
\ \\
I = \frac{3}{4} e^{2x} \left( 2x^2-2x+1\right) + C
$$

Quando tivermos um integrando sendo um produto entre uma função polinomial e uma função logarítmica, geralmente é mais fácil derivar o $\ln(x)$ do que integrá-lo, já que a própria integral de $\ln(x)$ é pelo método por partes. Sendo assim, colocamos $\ln(x)$ na coluna $u$. Mas surge uma questão: Por mais que derivarmos o $\ln(x)$ nunca encontraremos zero. Então, como saberemos quando parar com o processo?

Analisamos o grau $n$ do polinômio: a quantidade de derivações será igual a $n+1$. Em seguida fazemos o processo como os demais exemplos anteriores. Vejamos os exemplos $4$, $5$ e $6$.

Exemplo 4:

Calcular a integral $\displaystyle I = \int \ln(x)\ dx$.

Neste caso, fazemos $u=\ln(x)$ e $dv=dx$. O polinômio é de grau zero, ou seja $x^0=1$, e multiplica o $dx$. Devemos efetuar apenas uma derivação.

$$
I = \color{red}{+} \color{blue}{x \ln(x)} \color{red}{-} \color{green}{\int \frac{1}{x} \cdot x\ dx}\\
\ \\
I = x \ln(x) - \int \ dx\\
\ \\
I = x \ln(x) - x + C\\
\ \\
I = x(\ln(x) - 1) + C
$$

Exemplo 5:

Calcular a integral $\displaystyle I = \int x \ln(x)\ dx$.

Neste caso, fazemos $u=\ln(x)$ e $dv=x\ dx$. O polinômio é de grau $1$ e devemos efetuar duas derivações.

$$
I = \color{red}{+} \color{blue}{\frac{1}{2}x^2 \ln(x)} \color{red}{-} \color{blue}{\frac{1}{x} \cdot \frac{x^3}{6}} \color{red}{+} \color{green}{\int \left( -\frac{1}{x^2}\cdot \frac{x^3}{6} \right)\ dx} $$

$$
I = \frac{1}{2} x^2 \ln(x) - \frac{1}{6}x^2 - \frac{1}{6} \int x\ dx\\
\ \\
I = \frac{1}{2} x^2 \ln(x) - \frac{1}{6} x^2 - \frac{1}{12} x^2 + C\\
\ \\
I = \frac{1}{2}x^2 \ln(x) - \frac{1}{4}x^2 + C\\
\ \\
I = \frac{1}{4} x^2 \left( 2 \ln(x) - 1\right) + C
$$

Exemplo 6:

Calcular a integral $\displaystyle I = \int x^2 \ln(x)\ dx$.

Neste caso, fazemos $u=\ln(x)$ e $dv=x^2\ dx$. O polinômio é de grau $2$ e devemos efetuar três derivações.

$$
I = \color{red}{+} \color{blue}{\frac{x^3}{3} \ln(x)} \color{red}{-} \color{blue}{\frac{1}{x}\cdot \frac{x^4}{12}} \color{red}{+} \color{blue}{\left(-\frac{1}{x^2}\cdot \frac{x^5}{60} \right)} \color{red}{-} \color{green}{\int \frac{2}{x^3} \cdot \frac{x^5}{60}\ dx} $$

$$
I = \frac{x^3}{3}\ln(x)-\frac{x^3}{12}-\frac{x^3}{60}-\frac{1}{30} \int x^2 \ dx\\
\ \\
I = \frac{x^3}{3}\ln(x) - \frac{x^3}{10} - \frac{x^3}{90} + C\\
\ \\
I = \frac{x^3}{3}\ln(x) - \frac{x^3}{9}+C\\
\ \\
I = \frac{1}{9}x^3 \left( 3\ln(x)-1\right)+C
$$

Integrais onde as funções não são polinômios

Neste grupo, entram funções logarítmicas, exponenciais, trigonométricas e inversas.

Neste caso, para escolhermos as funções que representarão $u$ e $dv$, para $u$ podemos tentar seguir as prioridades abaixo, muito embora, nem sempre é a melhor escolha, mas serve como um ponto de partida:

• Logarítmicas
• Inversas
• Trigonométricas
• Exponenciais

Temos que observar que estas funções, por mais que a derivarmos, nunca serão zero. Então, quando parar?

Em alguns casos, quando seguimos o processo de derivação de $u$ e integração de $dv$, o produto da última linha acaba repetindo a função original (pode aparecer com sinal trocado ou multiplicado por alguma constante). Nestes casos, substituímos a função que se repete por $I$. Vejamos os exemplos de $7$, $8$ e $9$.

Exemplo 7:

Calcular a integral $\displaystyle I = \int e^x \ \cos(x)\ dx$.

Vamos considerar $u=\cos(x)$ e $dv=e^x\ dx$.

$$
I = \color{red}{+}\ \color{blue}{e^x \cos(x)} \color{red}{-} \color{blue}{(-\text{sen}(x)) e^x} \color{red}{+} \color{green}{\int (-\cos(x)) e^x \ dx} $$

$$
I = e^x \cos(x) + e^x \text{sen}(x) - \int e^x \cos(x)\ dx
$$

Vejam que o integrando $e^x\cos(x)$ é o mesmo da função original e podemos substituir por $I$. Assim:

$$
I = e^x(\text{sen}(x)+\cos(x)) - I + C\\
\ \\
2I = e^x(\text{sen}(x) + \cos(x) + C\\
\ \\
I = \frac{1}{2} e^x (\text{sen}(x)+\cos(x)) + C
$$

Exemplo 8:

Calcular a integral $\displaystyle \int e^{2x}\text{sen}(x)\ dx$.

Neste caso, como tem uma constante multiplicando o $x$ do exponencial $e^{2x}$, fica menos trabalhoso se adotarmos $u=e^{2x}$. Faça o teste com $dv = e^{2x}dx$.

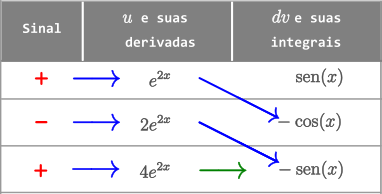
$$
I = \color{red}{+} \color{blue}{e^{2x}(-\cos(x))} \color{red}{-} \color{blue}{2e^{2x}(-\text{sen}(x))} \color{red}{+} \color{green}{\int4e^{2x}(-\text{sen}(x))\ dx} $$

$$
I = -e^{2x}\cos(x)+2e^{2x} \text{sen}(x)- 4 \int e^{2x}\text{sen}(x)\ dx\\
\ \\
I = e^{2x}(2 \text{sen}(x)-\cos(x))-4 \int e^{2x}\text{sen}(x)\ dx
$$

Vejam que o integrando $e^{2x}\text{sen}(x)$ é o mesmo que a função original. Assim:

$$
I = 2^{2x}(2 \text{sen}(x)-\cos(x))-4I + C\\
\ \\
5I = e^{2x}(2 \text{sen}(x)-\cos(x)) + C\\
\ \\
I = \frac{1}{5} e^{2x} (2 \text{sen}(x) - \cos(x))+C
$$

Para alguns casos de integrais, devemos aplicar o método de integração por partes repetidas vezes. O mesmo ocorre pelo método tabular. O próximo exemplo mostra como aplicar duas vezes o método tabular:

Exemplo 9:

Calcular a integral $\displaystyle I = \int \ln^2(x)\ dx$.

$$
I = \color{red}{+}\ \color{blue}{x \ln^2(x)} \color{red}{-} \color{green}{\int x \frac{2 \ln(x)}{x}\ dx}\\
\ \\
I = x \ln^2(x) - 2\int \ln(x)\ dx
$$

Para integrarmos $\ln(x)$ devemos utilizar o método tabular novamente. Vamos chamar de $\displaystyle J= \int \ln(x)\ dx$. Assim:

$$
J = \color{red}{+}\ \color{blue}{x \ln(x)} \color{red}{-} \color{green}{\int x \cdot \frac{1}{x} dx}\\
\ \\
J = x \ln(x) - \int dx\\
\ \\
J = x\ln(x) - x + C
$$

E finalmente:

$$
I = x\ln^2(x) - 2(x \ln(x)-x)+C\\
\ \\
I = x \ln^2(x)-2x \ln(x) + 2x + C\\
\ \\
I = x(\ln^2(x) - 2 \ln(x) + 2) + C
$$

Veja outros métodos de integração:

• Por partes
• Tabular
• Por substituição
• Por frações parciais
• Por substituição trigonométrica
• Integrais literais resolvidas
• Fórmulas de redução
• Por partes com 3 termos