O Teorema de Pitágoras é uma relação matemática que envolve os lados de um triângulo retângulo qualquer.
Por dedfinição, a hipotenusa é o lado do triângulo oposto ao ângulo reto do triangulo e os catetos são os lados adjacentes.
Na geometria euclidiana, o teorema afirma que o quadrado sobre a hipotenusa é igual à soma dos quadrados sobre os outros dois catetos. Matematicamente, podemos escrever:
$$c^2 = a^2 + b^2
$$

Esta demonstração do Teorema de Pitágoras não inicia a partir de um triângulo retângulo dado, mas sim de quatro triângulos retângulos, cuja hipotenusa vale $c$ e catetos iguais a $a$ e $b$.
Iniciamos construindo quatro triângulos congruentes cujas hipotenusas valem $c$ e catetos iguais a $a$ e $b$ e dispomo-os em ângulos iguais a $0º$, $90º$, $180º$ e $270º$:
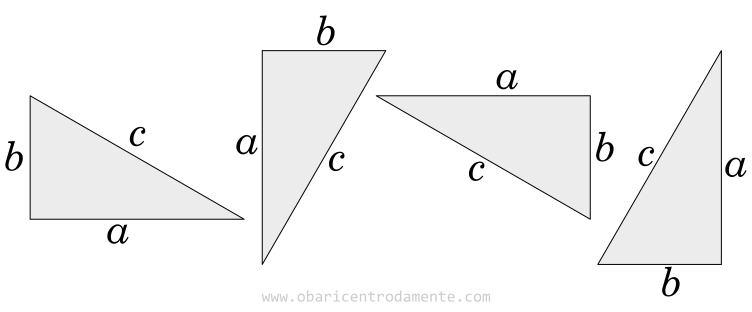
Em seguida, fazemos um arranjo entre estes estes triângulos de modo a formar um quadrado, cujos lados iguais a $c$, são as hipotenusas dos triângulos:

Construímos um quadrado de lado igual a $c$ e internamente temos outro quadrado de lado igual a $a-b$.
Até o momento temos as seguintes áreas:
- Área de cada triângulo retângulo: $\displaystyle A=\frac{ab}{2}$;
- Área de dos quatro triângulos: $\displaystyle A = \frac{4ab}{2}={2ab}$;
- Área do quadrado interno: $\displaystyle (a-b)^2$;
- Área do quadrado externo: $c^2$.
Voltamos À área do quadrado externo. Temos então que sua área é igual à área dos quatro triângulos mais a área do quadrado interno. Então:
$$c^2 = 2ab + (a-b)^2\\
\ \\
c^2 = 2ab + a^2 - 2ab + b^2\\
\ \\
c^2 = a^2 + b^2
$$
Como $c^2$ é a área de um quadrado sobre a hipotenusa de lado $c$, $b^2$ é a área de um quadrado sobre o lado $b$ e $a^2$ é a área de um quadrado sobre o lado $a$, podemos esboçar a figura:

- Veja este belo papel de parede com o Teorema de Pitágoras no blog do Professor Edigley Alexandre.


Postar um comentário