O método de Perigal para demonstrar o Teorema de Pitágoras, utiliza-se dos quadrados sobre os lados, divididos em partes tais que, rearranjando-as, completam o quadrado sobre a hipotenusa.
Vamos inicialmente abordar uma breve biografia de Perigal; em seguida uma explicação sobre seu método de dissecção e em seguida demonstrar algebricamente o Teorema de Pitágoras. Ao fim do artigo exite um link para download em pdf do método para que seja impresso, recortado a fim de que seja possível testar na prática se a soma dos quadrados dos catetos realmente é igual ao quadrado da hipotenusa.

Henry Perigal nasceu a 1 de abril de 1801 em Newington, Londres, Inglaterra e faleceu a 6 de junho de 1898.
Perigal descende de uma família huguenote que emigrou para a Inglaterra ainda no século XVII e era o mais velhos de seis irmãos. Depois de trabalhar como escriturário no Conselho Privado de Sua Majestade, tornou-se contador em uma corretora londrina na década de 1840.
Foi membro da London Mathematical Society de 1868 a 1897 e foi tesoureiro da Royal Meteorological Society por 45 anos, de 1853 a 1898, ano de sua morte. Foi membro da Royal Astronomical Society em 1850.
Frequentou a Royal Institution regularmente como visitante por muitos anos e finalmente tornou-se membro em 1895, aos 94 anos de idade.
Embora Perigal tenha vivido por muito tempo, seu pais viveu ainda mais, tornando-se um centenário.
Em seu livro Dissecções e Transposições Geométricas de 1891, Perigal forneceu uma prova do Teorema de Pitágoras baseado na ideia de dissecar dois quadrados sobre os lados menores em 5 partes e compor um quadrado igual ao quadrado que fica sobre a hipotenusa de um triângulo retângulo. Essa dissecção foi inserida em sua lápide.
Perigal também expressou a esperança de que métodos baseados em dissecações também resolvessem o problema de Tarski de quadratura do círculo por dissecções. esse problema mostrou-se impossível de resolver de maneira construtiva.
Além de se interessar por matemática, Perigal também sabia trabalhar com torno e realizou modelos de curvas matemáticas para Augustus De Morgan. Ele acreditava que a lua não girava em relação às estrelas fixas e usou seu conhecimento de movimento curvilíneo na tentativa de demonstrar essa crença outras pessoas.
A dissecção de Perigal
O Teorema de Pitágoras estabelece que em um triângulo retângulo a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os outros dois lados.
Iniciamos construindo quadrados sobre os lados do triângulo retângulo $ABC$. No quadrado $ACDE$ sobre o cateto maior, traçamos as diagonais para determinar o centro $O$ do quarado. Em seguida, traçamos o segmento $FG$ paralelo à hipotenusa e em seguida, traçamos o segmento $HI$ perpendicular a $FG$. O quadrado $ACDE$ é dissecado em quatro partes congruentes que, somado ao quadrado $BCJK$ sobre o cateto menor, é igual ao quadrado $ACLM$ sobre a hipotenusa.

Demonstração:
Temos que mostrar que o Método de Perigal corrobora o teorema pitagórico:
\begin{equation*}a^2 + b^2 = c^2 \tag{1}
\end{equation*}
O ponto $O$ é o centro da circunferência circunscrita ao quadrado $ABDE$ e, portanto, também é o seu centro, definido pela intersecção suas diagonais $AD$ e $CE$.
O segmento $FG$, traçado paralelamente à hipotenusa $c$ do triângulo retângulo $ABC$, passa pelo centro $O$ do quadrado $ACDE$, dividindo-o em duas partes congruentes.
Quando traçamos o segmento $HI$ através do centro $O$ e perpendicular à $FG$, dividimos o quadrado $ACDE$ em quatro quadriláteros congruentes.
Os segmentos $EF=DI=CG=AH=x$ e como o segmento $AC=AE=b$, temos que $AH=b-x$.
Podemos observar que o quadrilátero $ABGF$ é um paralelogramo, uma vez que, por construção, os lados opostos são paralelos.
Desta forma, temos que o lado $BG$ do paralelogramo é igual à $AF$. Assim:
\begin{equation*}a + x = b - x\\
\ \\
a = b - 2x \tag{2}
\end{equation*}
Analisando o triângulo $EFI$, onde um dos catetos mede $x$ e o outro $b-x$, vamos encontrar a hipotenusa $e$ em função de $b$ e $x$ para que posteriormente possamos determinar o valor de $c$:
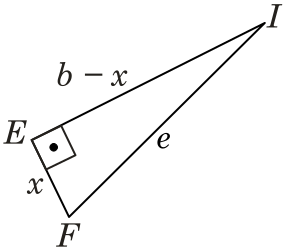
\begin{equation*}
e^2 = x^2 + (b-x)^2\\
\ \\
e^2 = x^2 + b^2 - 2bx + x^2\\
\\
e^2 = 2x^2 - 2bx + b^2 \tag{3}
\end{equation*}
O segmento $e$ também é a hipotenusa dos triângulo isósceles $FOI$:
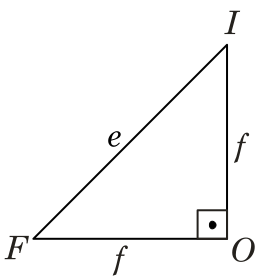
\begin{equation*}
e^2 = f^2 + f^2\\
\ \\
2x^2 -2bx + b^2 = 2f^2\\
\ \\
f^2 = \frac{2x^2 -2bx + b^2}{2}\\
\ \\
f = \sqrt{\frac{2x^2 - 2bx +b^2}{2}} \tag{4}
\end{equation*}
A hipotenusa $c$ do triângulo $ABC$ também é o lado do paralelogramo $ABGF$, de modo que $c=2f$, assim:
\begin{equation*}c = 2f\\
\ \\
c = 2\ \sqrt{\frac{2x^2 - 2bx +b^2}{2}}\\
\ \\
c = \sqrt{4x^2 - 4bx + 2b^2} \tag{5}
\end{equation*}
Aplicando os resultados obtidos em $(2)$ e $(5)$ em $(1)$, temos:
\begin{equation*}a^2 + b^2 = c^2\\
\ \\
(b-2x)^2 + b^2 = 4x^2 - 4bx + 2b^2\\
\ \\
4x^2 - 4bx + 2b^2 = 4x^2 -4bx + 2b^2 \tag{6}
\end{equation*}
A igualdade $(6)$ mostra que a área do quadrado sobre a hipotenusa $c$ é igual à som das áreas dos quadrados construídos sobre os catetos $a$ e $b$.
Quebra-cabeça:
Uma forma de visualizar esse método das dissecções é imprimindo a imagem abaixo, recortar as partes que compões os catetos e em seguida montá-lo sobre a hipotenusa. Essa aplicação pode ser trabalhada em sala de aula facilmente.

Façam o download do arquivo pdf contendo a imagem para recortar, assim como todas as imagens acima.
Acessem o blog do professor Edigley Alexandre e leia o artigo 50 curiosidades até hoje não conhecidas relacionadas ao teorema de Pitágoras.
Links para este artigo:
- http://bit.ly/Perigal
- https://www.obaricentrodamente.com/2018/11/teorema-de-pitagoras-metodo-de-perigal.html


Postar um comentário