Integração por Substituição Trigonométrica

Há meios diferentes para integrar uma função e para cada integral, devemos identificar qual o melhor dos métodos a aplicar. Somente resolvendo diversos exemplos para podermos nos familiarizar com cada um desses métodos.

A substituição trigonométrica é uma técnica de integração muito utilizada quando ocorre integrandos algébricos. Ela se baseia no fato que identidades trigonométricas muitas vezes possibilitam a substituição de um função algébrica por uma função trigonométrica, que pode ser mais facilmente integrada.

No caso de integração por substituição trigonométrica, um integrante que contenha uma das formas:

\begin{gather*}
\sqrt{a^2-x^2} \tag{I} \\
\ \\
\sqrt{a^2+x^2}\tag{II}\\
\ \\
\sqrt{x^2-a^2}\tag{III}
\end{gather*}

sendo $a$ uma constante positiva e não tendo nenhum outro fator irracional, pode ser transformado numa integral trigonométrica mais familiar, utilizando substituições trigonométricas ou com o emprego de uma nova variável.

Para os três casos acima, utilizamos as identidades trigonométricas:

\begin{gather*}
1-\text{sen}^2(\theta) = \cos^2(\theta) \tag{1}\\
\ \\
1+\text{tg}^2(\theta) = \text{sen}^2(\theta)\tag{2}\\
\ \\
\text{sec}^2(\theta)-1 = \text{tg}^2(\theta)\tag{3}
\end{gather*}
Vamos ver dada um desses casos separadamente.

Caso I

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{a^2-x^2}$, fazemos a mudança de variável de $x$ para $\theta$. A substituição deve ser apropriada e fica melhor observada no triângulo retângulo:

Temos que:
\begin{equation*}
\text{sen}(\theta) = \frac{x}{a}\\
\ \\
x = a \ \text{sen}(\theta)
\end{equation*}

Assim, $x = a\ \text{sen}(\theta)$ substitui $\displaystyle \sqrt{a^2-x^2}$ por $a\ \cos(\theta)$, pois:

\begin{equation*}
a^2 - x^2 = a^2 - \left(a\ \text{sen}(\theta)\right)^2\\
\ \\
a^2 - x^2 = a^2 - a^2\  \text{sen}^2(\theta)\\
\ \\
a^2 - x^2 = a^2 \left(1-\text{sen}^2(\theta)\right)
\end{equation*}

E pela identidade trigonométrica dada em $(1)$, obtemos:

\begin{equation*}
a^2 - x^2 = a^2\ \cos^2(\theta)
\end{equation*}

Extraindo a raiz de ambos os membros da equação, obtemos:

\begin{equation*}
\sqrt{a^2-x^2} = a\ \cos(\theta)
\end{equation*}
Justificando a substituição.

Caso II

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{a^2+x^2}$, fazemos a mudança de variável de $x$ para $\theta$. Observando o triângulo retângulo:

Temos que:
\begin{equation*}
\text{tg}(\theta) = \frac{x}{a}\\
\ \\
x = a\ \text{tg}(\theta)
\end{equation*}

Assim, $x = a\ \text{tg}(\theta)$ substitui $\displaystyle \sqrt{a^2 +x^2}$ por $a\ \text{sec}(\theta)$, pois:

\begin{equation*}
a^2 + x^2 = a^2 + \left(a\ \text{tg}(\theta)\right)^2\\
\ \\
a^2 + x^2 = a^2 + a^2\ \text{tg}^2(\theta)\\
\ \\
a^2 + x^2 = a^2 \left( 1 + \text{tg}(\theta) \right)
\end{equation*}

E pela identidade trigonométrica da em $(2)$, obtemos:

\begin{equation*}
a^2 + x^2 = a^2\ \text{sec}^2(\theta)
\end{equation*}

Extraindo a raiz de ambos os membros da equação acima, obtemos:

\begin{equation*}
\sqrt{a^2+x^2} = a\ \text{sec}(\theta)
\end{equation*}
Justificando a substituição.

Caso III

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{x^2-a^2}$, fazemos a mudança de variável de $x$ para $\theta$. Observando o triângulo retângulo:

Temos que:
\begin{equation*}
\text{sec}(\theta) = \frac{x}{a}\\
\ \\
x = a\ \text{sec}(\theta)
\end{equation*}

Assim, $x=a\ \text{sec}(\theta)$ substitui $\displaystyle \sqrt{x^2-a^2}$ por $a\ \text{tg}(\theta)$, pois:

\begin{equation*}
x^2 - a^2 = \left(a\ \text{sec}(\theta)\right)^2 - a^2\\
\ \\
x^2 - a^2 = a^2 \text{sec}^2(\theta) - a^2\\
\ \\
x^2 - a^2 = a^2 \left(\text{sec}^2(\theta)-1\right)
\end{equation*}

E pela identidade trigonométrica dada em $(3)$, obtemos:

\begin{equation*}
x^2-a^2 = a^2 \ \text{tg}^2(\theta)
\end{equation*}

Extraindo a raiz de ambos os membros da equação, obtemos:

\begin{equation*}
\sqrt{x^2-a^2} = a\ \text{tg}(\theta)
\end{equation*}
Justificando a substituição.

Com base nos resultados obtidos acima, podemos montar uma tabela:

Vejam que, para representar graficamente as substituições sugeridas no triângulo retângulo, o radical ficará sempre no lado do triângulo que não é utilizado pela relação trigonométrica:

• Caso I: Usa-se $x = a\ \text{sen}(\theta)$; logo, o radical aparece no cateto adjacente a $\theta$;
• Caso II: Usa-se $a\ \text{tg}(\theta)$ ; logo, o radical aparece na hipotenusa;
• Caso III: Usa-se $a\ \text{sec}(\theta)$; logo, o radical aparece no cateto oposto a $\theta$.

Exemplo 1:

Calcular a integral $\displaystyle \int \frac{\sqrt{a^2-x^2}}{x}\ dx$.

Essa é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
\begin{gather*}
\text{sen}(\theta) = \frac{x}{a}\\
\ \\
x = a\ \text{sen}(\theta) \tag{a}\\
\ \\
dx = a\ \cos(\theta)\ d\theta \tag{b}\\
\ \\
\sqrt{a^2 - x^2} = a\ \cos(\theta)\tag{c}
\end{gather*}
Assim, seja a integral:
\begin{equation*}
I = \int \frac{\sqrt{a^2-x^2}}{x}\ dx\\
\ \\
I = \int \frac{a\ \cos(\theta)}{a\ \text{sen}(\theta)}\ a\ \cos(\theta)\ d\theta\\
\ \\
I = a \int \frac{\cos^2(\theta)}{\text{sen}(\theta)}\ d\theta\\
\ \\
I = \ \int \frac{1 - \text{sen}^2(\theta)}{\text{sen}(\theta)}\ d\theta\\
\ \\
I = a \int \left( \frac{1}{\text{sen}(\theta)}-\text{sen}(\theta) \right)\ d\theta\\
\ \\
I =  a \int \left( \text{cosec}(\theta) - \text{sen}(\theta)\right)\ d\theta\\
\ \\
I = -a\ \ln \left( \text{cosec}(\theta) + \text{cotg}(\theta)\right) + a\ \cos(\theta) + C
\end{equation*}

Devemos agora reescrever o resultado em termos da variável original $x$. Observando o triângulo retângulo, devemos encontrar as relações trigonométricas que aparecem no resultado acima. assim:

\begin{equation*}
\text{cosec}(\theta) = \frac{a}{x}\\
\ \\
\text{cotg}(\theta) = \frac{\sqrt{a^2-x^2}}{x}\\
\ \\
\cos(\theta) = \frac{\sqrt{a^2-x^2}}{a}
\end{equation*}
Assim:
\begin{equation*}
I = -a \ln \left( \frac{a}{x} + \frac{\sqrt{a^2-x^2}}{x}\right)  + a\ \frac{\sqrt{a^2-x^2}}{a} + C\\
\ \\
I =\sqrt{a^2-x^2} - a \ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right) + C\\
\ \\
I = \sqrt{a^2 - x^2} - \ln \left(a + \sqrt{a^2-x^2} \right) + a\ \ln (x) + C
\end{equation*}

Exemplo 2:

Calcular a integral $\displaystyle \int \frac{dx}{\sqrt{a^2+x^2}}$.

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
\begin{gather*}
\text{tg}(\theta) = \frac{x}{a}\\
\ \\
x = a\ \text{tg}(\theta) \tag{a}\\
\ \\
dx = a\ \text{sec}^2(\theta)\ d\theta \tag{b}\\
\ \\
\sqrt{a^2+x^2} = a\ \text{sec}(\theta) \tag{c}
\end{gather*}
Assim, seja a integral:
\begin{equation*}
I = \int \frac{dx}{\sqrt{a^2+x^2}}\\
\ \\
I = \int \frac{a\ \text{sec}^2(\theta)}{a\ \text{sec}(\theta)}\ d\theta \\
\ \\
I = \int \text{sec}(\theta)\ d\theta\\
\ \\
I = \ln \left( \text{sec}(\theta) + \text{tg}(\theta) \right)  + C
\end{equation*}

Vamos agora reescrever o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos as relações:

\begin{equation*}
\text{sec}(\theta) = \frac{\sqrt{a^2+x^2}}{a}\\
\ \\
\text{tg}(\theta) = \frac{x}{a}
\end{equation*}
Assim:
\begin{equation*}
I = \ln \left( \frac{\sqrt{a^2+x^2}}{a}+\frac{x}{a} \right) + C\\
\ \\
I = \ln \left(\frac{\sqrt{a^2+x^2}+x}{a} \right) + C\\
\ \\
I = \ln \left(\sqrt{a^2+x^2}+x\right) - \ln(a) + C
\end{equation*}

Como $C$ é uma constante arbitrária e $\ln(a)$ também é uma constante, podemos reescrever o resultado como:

\begin{equation*}
I = \ln \left( \sqrt{a^2+x^2}+x \right)+ C
\end{equation*}

Exemplo 3:

Calcular a integral $\displaystyle \int \frac{\sqrt{x^2-a^2}}{x}\ dx$.

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim escrevemos:
\begin{gather*}
\text{sec}(\theta) = \frac{x}{a}\\
\\\
x = a\ \text{sec}(\theta) \tag{a}\\
\ \\
dx = a\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta \tag{b} \\
\ \\
\sqrt{x^2-a^2} = a\ \text{tg}(\theta) \tag{c}
\end{gather*}
Assim, seja a integral:
\begin{equation*}
I = \int \frac{\sqrt{x^2-a^2}}{x}\ dx\\
\ \\
I = \int \frac{a\ \text{tg}(\theta)}{a\ \text{sec}(\theta)}\ a \ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta\\
\ \\
I = \int a\ \text{tg}^2(\theta)\ d\theta\\
\ \\
I = a \int \left(\text{sec}^2(\theta)-1\right)\ d\theta\\
\ \\
I = a\ \text{tg}(\theta) - a\ (\theta) + C
\end{equation*}

Vamos reescrever o resultado em termos da variável original $x$. Observando o triângulo encontramos as relações:

\begin{equation*}
\text{tg}(\theta) = \frac{\sqrt{x^2-a^2}}{a}\\
\ \\
\theta = \text{arctg}\left( \frac{\sqrt{x^2-a^2}}{a} \right)
\end{equation*}
Assim:
\begin{equation*}
I = a\ \frac{\sqrt{x^2-a^2}}{a} - a\ \text{arctg}\left( \frac{\sqrt{x^2-a^2}}{a} \right)+C\\
\ \\
I = \sqrt{x^2-a^2} - a\ \text{arctg} \left( \frac{\sqrt{x^2-a^2}}{a} \right) + C
\end{equation*}

Exemplo 4:

Calcular a integral $\displaystyle \int \frac{dx}{x^2\sqrt{16-x^2}}$.

Esta é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
\begin{gather*}
\text{sen}(\theta) = \frac{x}{4}\\
\ \\
x = 4\ \text{sen}(\theta) \tag{a}\\
\ \\
dx = 4\ \cos(\theta)\ d\theta \tag{b}\\
\ \\
\sqrt{16-x^2} = 4\ \cos(\theta) \tag{c}
\end{gather*}
Seja a integral:
\begin{equation*}
I = \frac{dx}{x^2 \sqrt{16-x^2}}\\
\ \\
I = \frac{4\ \cos(\theta)\ d\theta}{\left(4\ \text{sen}(\theta)\right)^2\ 4\ \cos(\theta)}\\
\ \\
I = \frac{1}{16} \int \frac{d\theta}{\text{sen}^2(\theta)}\\
\ \\
I = \frac{1}{16} \int \text{cosec}^2(\theta)\ d\theta\\
\ \\
I = -\frac{1}{16} \text{cotg}(\theta)\ d\theta +C
\end{equation*}

Agora, reescrevemos o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos a relação:

\begin{equation*}
\text{cotg}(\theta) = \frac{\sqrt{16-x^2}}{x}
\end{equation*}
Assim:
\begin{equation*}
I = -\frac{\sqrt{16-x^2}}{16x} + C
\end{equation*}

Exemplo 5:

Calcular a integral $\displaystyle \int \frac{dx}{x^2 \sqrt{4+x^2}}$.

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

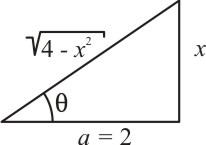
Assim, escrevemos:
\begin{gather*}
\text{tg}(\theta) = \frac{x}{2}\\
\ \\
x = 2\ \text{tg}(\theta) \tag{a}\\
\ \\
dx = 2\ \text{sec}^2(\theta)\ d\theta \tag{b}\\
\ \\
\sqrt{4+x^2} = 2\ \text{sec}(\theta) \tag{c}
\end{gather*}
Seja a integral:
\begin{equation*}
I = \int \frac{dx}{x^2 \sqrt{4+x^2}}\\
\ \\
I = \int \frac{2\ \text{sec}^2(\theta)\ d\theta}{\left(2\ \text{tg}(\theta)\right)^2\ 2\ \text{sec}(\theta)}\\
\ \\
I = \frac{1}{4} \int \frac{\text{sec}(\theta)}{\text{tg}^2(\theta)}\ d\theta\\
\ \\
I = \frac{1}{4} \int \text{cosec}^2(\theta)\ \cos(\theta)\ d\theta\\
\ \\
I = \frac{1}{4} \text{cosec}(\theta)+C
\end{equation*}

Reescrevendo o resultado em termos da variável original $x$ e utilizando as relações observadas no triângulo retângulo, fazemos:

\begin{equation*}
\text{cosec}(\theta) = \frac{4+x^2}{x}
\end{equation*}
Assim:
\begin{equation*}
I = \frac{1}{4} \cdot \frac{\sqrt{4+x^2}}{x}+C\\
\ \\
I = \frac{\sqrt{4+x^2}}{4x}+C
\end{equation*}

Exemplo 6:

Calcular a integral $\displaystyle \int \frac{dx}{x^3 \sqrt{x^2-25}}$.

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
\begin{gather*}
\text{sec}(\theta) = \frac{x}{5}\\
\ \\
x = 5\ \text{sec}(\theta) \tag{a}\\
\ \\
dx = 5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta \tag{b}\\
\ \\
\sqrt{x^2-25} = 5\ \text{tg}(\theta) \tag{c}
\end{gather*}
Seja a integral:
\begin{equation*}
I = \int \frac{dx}{x^3 \sqrt{x^2-25}}\\
\ \\
I = \int \frac{5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta}{(5\ \text{sec}(\theta))^3 \ 5\ \text{tg}(\theta)}\\
\ \\
I = \int \frac{5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta}{125\ \text{sec}^3(\theta)\ 5\ \text{tg}(\theta)}\\
\ \\
I = \frac{1}{125} \int \frac{d\theta}{\text{sec}^2(\theta)}\\
\ \\
I = \frac{1}{125} \int \cos^2(\theta)\ d\theta\\
\end{equation*}

A integral de $\cos^2(\theta)$ é $\displaystyle \frac{1}{2}(\theta + \text{sen}(\theta)\ \cos(\theta))$, assim:

\begin{equation*}
I = \frac{1}{125} \cdot \frac{1}{2}(\theta + \text{sen}(\theta)\ \cos(\theta))+C\\
\ \\
I = \frac{1}{250} (\theta + \text{sen}(\theta)\ \cos(\theta))+C
\end{equation*}

Agora, representamos o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos as relações:

\begin{equation*}
\text{sen}(\theta) = \frac{\sqrt{x^2-25}}{x}\\
\ \\
\cos(\theta) = \frac{5}{x}\\
\ \\
\theta = \text{arctg} \left( \frac{5}{\sqrt{x^2-25}} \right)
\end{equation*}
Assim:
\begin{equation*}
I = \frac{1}{250} \left( \text{arctg}\left( \frac{5}{\sqrt{x^2-25}} \right) + \frac{\sqrt{x^2-25}}{x}\cdot \frac{5}{x} \right) + C\\
\ \\
I = \frac{1}{250} \left( \frac{5\sqrt{x^2-25}}{x^2} + \text{arctg} \left( \frac{5}{\sqrt{x^2-25}} \right) \right) + C
\end{equation*}

Exemplo 7:

Para ilustrar o uso desse método, vamos determinar a equação da tractriz, que é uma curva definida pela trajetória de um objeto arrastado ao longo de um plano horizontal por um fio de comprimento constante quando a outra extremidade do fio se move ao longo de uma reta no plano. A palavra tractriz provém do latim tractum, que significa "draga". Vamos considerar um plano formado por eixos ortogonais $x\ y$ e o objeto comece no ponto $(a,\ 0)$ com a outra extremidade do fio na origem. Se esta se move para cima ao longo do eixo dos $y$:

o fio será sempre tangente à curva e o comprimento da tangente entre o eixo dos $y$ e o ponto de contato será sempre igual a $a$. O coeficiente angular da tangente é dado pela fórmula:

\begin{equation*}
\frac{dy}{dx} = -\frac{\sqrt{a^2-x^2}}{x}
\end{equation*}

Separando as variáveis e usando o resultado do exemplo 1, temos:

\begin{equation*}
y = - \int \frac{\sqrt{a^2-x^2}}{x}\ dx \\
\ \\
y = a\ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right) - \sqrt{a^2-x^2}+C
\end{equation*}
Quando $x=a$, $y=0$ e $C=0$. Logo:
\begin{equation*}
y = a\ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right)-\sqrt{a^2-x^2}
\end{equation*}
que é a equação da tractriz.

Se as extremidades do fio movem-se para baixo no eixo dos $y$, então uma outra parte da curva é gerada. Se girarmos essas duas partes em torno do eixo dos $y$, a superfície resultante será uma pseudo-esfera, com forma de uma "trombeta dupla".

Tente resolver estes exercícios:

\begin{equation*}
1) \qquad \int \frac{x^3}{\sqrt{9-x^2}}\ dx \\
\ \\
2) \qquad \int \frac{x^2}{(4-x^2)^{3/2}}\ dx\\
\ \\
3) \qquad \int \frac{dx}{x^2\ \sqrt{x^2-9}}\\
\ \\
4) \qquad \int \frac{dx}{x^3\ \sqrt{x^2-4}}\\
\ \\
5) \qquad \int \sqrt{9-4x^2}\ dx
\end{equation*}

Links para este artigo:

• http://bit.ly/Subst-Trig
• https://www.obaricentrodamente.com/2012/06/integracao-por-substituicao.html

Referências:

• Cálculo com Geometria Analítica V1 - Simmons
• Cálculo V1 - Munen & Foulis
• Cálculo Diferencial e Integral - Frank Ayres Jr

Veja mais:

• Integração por Frações Parciais – Fatores Lineares 
• Integração por Frações Parciais – Fatores Quadráticos Irredutíveis 
• Método de Integração por Substituição 
• Método de Integração por Partes