Introdução: Um pouco de História
Houve um momento na História da Matemática em que a necessidade de expressar a raiz de um número negativo se tornou fundamental. Em equações quadráticas do tipo:\begin{equation*}
ax^2+bx+c=0
\end{equation*}
Temos uma fórmula fechada para sua resolução, que é a fórmula para equações de $2^\circ$ grau:
\begin{equation*}
x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}
\end{equation*}
Sendo $\displaystyle \Delta = b^2-4ac$.
O número $\Delta$ é o discriminante da equação e através dele podemos saber quantas raízes a equação de segundo grau possui:
Se $\Delta > 0$, temos $2$ raízes reais.
Se $\Delta = 0$, temos 1 raiz real.
Se $\Delta < 0$, não temos nenhuma raiz real e aqui que se encontrava o problema: Como expressar a raiz de $\Delta$ se $\Delta < 0$? Isso implicaria em dizer que: qual o número elevado ao quadrado resulta um número negativo?
Então, se tivermos a equação:
\begin{equation*}
x^2-4x+5=0\\
x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
x=\frac{4 \pm \sqrt{16-20}}{2}\\
x=\frac{4 \pm \sqrt{-4}}{2}
\end{equation*}
Vemos que caímos num caso particular em que a fórmula para a equação de $2^\circ$ grau não encontra raízes reais. Para contornar este problema, Bombelli admitiu que:
\begin{equation*}
\sqrt{-4} = \sqrt{4 \cdot (-1)} = 2\sqrt{-1}
\end{equation*}
Assim, considerando um novo tipo de número.
Leonhard Euler $(1707 – 1783)$ usou em $1777$ a letra $i$ para representar o número $\sqrt{-1}$, chamando-o de unidade imaginária, pois $i^2 = -1$.
Logo, seria possível encontrar uma solução para a equação:
\begin{equation*}
x=\frac{4\pm \sqrt{-4}}{2}
\end{equation*}
Fazemos:
\begin{equation*}
x=2 \pm \frac{\sqrt{4\cdot (-1)}}{2} = 2 \pm \frac{2 \sqrt{-1}}{2} = 2 \pm \sqrt{-1} = 2 \pm i
\end{equation*}
Surgiu, assim, um novo tipo de número, chamado por Gauss de Número Complexo, sendo expresso por:
\begin{equation*}
a+bi
\end{equation*}
Gauss, por volta de $1800$, associou a cada número na forma $a + bi$ um ponto $P$ do plano cartesiano, definido pelo par ordenado $(a, b)$:
[Figura 1]
Consequentemente, foi criado um novo conjunto numérico chamado de Conjunto dos Números Complexos e podemos fazer uma representação por diagramas de Venn:
[Figura 2]
Elementos do Conjunto Complexo
Um número complexo costuma-se ser simbolizado pela letra $z$. Qualquer elemento de $z$ de $\mathbb{C}$ tem a forma:\begin{equation*}
z = a+bi
\end{equation*}
com $a$ e $b$ $\in \mathbb{R}$, sendo $a$ a parte real $(\text{Re}(z))$ e $b$ a parte imaginária $(\text{Im}(z))$
Oposto de um Número Complexo
O oposto de um número complexo $z=a+bi$ é o número complexo:\begin{equation*}
-z = -a - bi
\end{equation*}
Igualdade de Números Complexos
Dois números complexos $z_1 = a+bi$ e $z_2 = c+di$ são iguais, se, e somente se $a=c$ e $b=d$, de modo que:\begin{equation*}
a+bi = c+di \Leftrightarrow a=c~\text{e}~b=d
\end{equation*}
Assim:
\begin{equation*}
\text{Re}(z_1) = \text{Re}(z_2) \Leftrightarrow a=c\\
\text{Im}(z_1) = \text{Im}(z_2) \Leftrightarrow b=d
\end{equation*}
Adição de Números Complexos
Dado dois números complexos $z_ 1 = a + bi$ e $z_2 = c + di$, temos que:\begin{equation*}
z_1 + z_2 = a+bi + a+di\\
z_1 + z_2 = (a+c) + i(b+d)\\
z_1+z_2 = [\text{Re}(z_1) + \text{Re}(z_2)] + i[\text{Im}(z_1) + \text{Im}(z_2)]
\end{equation*}
Subtração de Números Complexos
Dado dois números complexos $z_ 1 = a + bi$ e $z_2 = c + di$, temos que:\begin{equation*}
z_1 - z_2 = (a+bi) - (a+di)\\
z_1 - z_2 = a+bi - c - di\\
z_1 - z_2 = (a-c) + i(b-d)\\
z_1 - z_2 = [\text{Re}(z_1) - \text{Re}(z_2)] + i[\text{Im}(z_1) - \text{Im}(z_2)]
\end{equation*}
Conjugado de um Número Complexo
Dado um número complexo $z = a + bi$, o conjugado de $z$ é denominado por $\overline{z}$ e é dado por:\begin{equation*}
\overline{z} = a-bi \Leftrightarrow z = a+bi
\end{equation*}
Notem que:
\begin{equation*}
z \cdot \overline{z} = (a+bi) (a-bi) = a^2 - abi + abi - b^2i^2 = a^2 - b^2i^2
\end{equation*}
Mas $i^2=-1$, logo:
\begin{equation*}
z \cdot \overline{z} = a^2 + b^2
\end{equation*}
Multiplicação de Números Complexos
Dados dois números complexos $z_ 1 = a + bi$ e $z_2 = c + di$, o produto $z_1 \cdot z_2$ é dado por:\begin{equation*}
z_1 \cdot z_2 = (a+bi)(c+di) = ac + adi + cbi + bdi^2
\end{equation*}
Mas $i^2=-1$, logo:
\begin{equation*}
z_1 \cdot z_2 = ac + adi + cbi -bd\\
z_1 \cdot z_2 = (ac - bd)(ad + bc)i
\end{equation*}
Divisão de Números Complexos
Dado dois números complexos $z_1 = a + bi$ e $z_2 = c + di \neq 0$, o quociente $z_1 / z_2$ é obtido multiplicando ambos os termos pelo conjugado do divisor:\begin{equation*}
\frac{z_1}{z_2} = \frac{z_1}{z_2} \cdot \frac{\overline{z_2}}{\overline{z_2}} = \frac{a+bi}{c+di}\cdot \frac{c-di}{c-di} = \frac{ac - adi + cbi - bdi^2}{c^2 - cdi + cdi - d^2i^2}= \frac{ac - adi + cbi + bd}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}
\end{equation*}
Separando a parte Real da Imaginária, obtemos:
\begin{equation*}
\frac{z_1}{z_2} = \frac{ac + bd}{c^2 + d^2} + \frac{bc - ad}{c^2 + d^2}i
\end{equation*}
Inverso de um Número Complexo
Dado um número complexo não-nulo $z = a + bi$, o inverso deste número é dado por:\begin{equation*}
z^{-1} = \frac{1}{z} = \frac{1}{a+bi}
\end{equation*}
Ainda podemos escrever $z ^{– 1}$ como:
\begin{equation*}
z^{-1} = \frac{1}{a+bi} \cdot \frac{a-bi}{a-bi} = \frac{a-bi}{a^2 + b^2}
\end{equation*}
Potências de $i$ com Expoente Natural
Com relação às potências de $i$ com expoente natural, temos que:\begin{matrix}
i^0 &=& 1\\
i^1 &=& i&&&&\\
i^2 &=& -1&&&&\\
i^3 &=& i^2 \cdot i &=& -1 \cdot i &=& -i\\
i^4 &=& i^2 \cdot i^2 &=& (-1) \cdot (-1) &=& 1\\
i^5 &=& i^4 \cdot i &=& 1 \cdot i &=& i\\
i^6 &=& i^4 \cdot i^2 &=& 1 \cdot (-1) &=& -1\\
i^7 &=& i^6 \cdot i &=& -1 \cdot i &=& -i\\
i^8 &=& i^4 \cdot i^4 &=& 1\cdot 1 &=& 1
\end{matrix}
Percebemos que as potências se repetem de $4$ em $4$. Então, para calcular indicaremos $q$ como quociente e $R$ como resto da divisão de $n$ por $4$:
Daqui temos que $n = 4q + R$. Logo:
\begin{equation*}
i^n = i^{4q+R} =i^{4q} \cdot i^{R} = (i^4)^q \cdot i^R = 1^q \cdot i^R
\end{equation*}
Logo:
\begin{equation*}
i^n = i^R
\end{equation*}
Portanto, para calcularmos $i^n$, basta calcular $i^R$, onde $R$ é o resto da divisão de $n$ por $4$.
Plano de Argand–Gauss
Gauss associou a cada número $z = a + bi$, um ponto $P$ do Plano Cartesiano. A parte Real $(Re)$ do complexo é representada por um ponto no eixo horizontal e este é chamado de Eixo Real. A parte Imaginária $(Im)$, por sua vez, é representada por um ponto no eixo vertical, chamado de Eixo Imaginário. O ponto $P$, correspondente ao número complexo $z = a + bi$ é chamado de imagem ou afixo de $z$.A interpretação geométrica dos complexos foi descoberta em $1797$ por Caspar Wessel $(1745 – 1818)$, mas somente em $1806$, o matemático suíço Jean Robert Argand $(1768 – 1822)$ publicou um artigo sobre a representação gráfica dos números complexos. Gauss já havia concebido tal representação, mas só a publicou $30$ anos após a publicação de Wessel. Hoje, o plano dos números complexos é conhecido com Plano de Gauss ou Plano de Argand–Gauss e é representado como:
[Figura 3: Plano de Argand-Gauss]
Módulo e Argumento de um Número Complexo
No Plano de Gauss, a distância da origem até o ponto $P$ é chamada de módulo e representada por $|z|$, indicada na figura abaixo pela letra grega $\rho$ (Rô):
[Figura 4: módulo]
Para calcularmos a distância $\rho$, aplicamos o teorema pitagórico no triângulo $OaP$:
\begin{equation*}
\rho ^2 = a^2 + b^2\\
\rho = \sqrt{a^2 + b^2}
\end{equation*}
Algumas propriedades podem ser destacadas:
$P1)$ $|z| \geq 0$
$P2)$ $|z_1 \cdot z_2| = |z_1| \cdot |z_2|$
$P3)$ $|z| = 0 \Longrightarrow z=0$
$P4)$ $|\overline{z}| = |z|$
$P5)$ $\displaystyle \left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|}$
$P6)$ $\displaystyle |z|^n = |z^n|$
O ângulo formado pela reta suporte de $OP$ e o Eixo Real é denominado por $theta$, sendo $0 \leq \theta \leq 2\pi$ e é chamado de argumento de $z$, para $z \neq 0$ e indicamos por $\text{ARG}(z)$. Podemos escrever:
\begin{equation*}
\theta = \text{ARG}(z)
\end{equation*}
Tomando o triângulo retângulo $OaP$ da figura $4$, temos:
[Figura 5: triângulo retângulo]
Daqui obtemos as relações:
\begin{equation*}
\text{sen}(\theta) = \frac{b}{\rho} = \frac{b}{|z|} = \frac{b}{\sqrt{a^2+b^2}}\\
\cos(\theta) = \frac{1}{\rho} = \frac{1}{|z|} = \frac{a}{\sqrt{a^2+b^2}}\\
\text{tg}(\theta) = \frac{b}{a}
\end{equation*}
Forma Trigonométrica ou Polar dos Números Complexos
Seja o número complexo em sua forma algébrica $z = a + bi$, sendo $z \neq 0$. Das relações trigonométricas acima, observadas na figura $5$, temos que:\begin{equation*}
\text{sen}(\theta) = \frac{b}{\rho} \Longrightarrow b = \rho \cdot \text{sen}(\theta)\\
\cos(\theta) = \frac{a}{\rho} \Longrightarrow a = \rho \cdot \cos(\theta)
\end{equation*}
Se substituirmos essas relações na forma algébrica de $z=a+bi$ obteremos:
\begin{equation*}
z = a + bi\\
z = \rho \cdot \cos(\theta) + \rho \cdot \text{sen}(\theta) i\\
z = \rho \left(\cos(\theta) + i ~\text{sen}(\theta)\right)
\end{equation*}
A forma polar de $z$ é muito útil para efetuarmos potenciação e radiciação de números complexos.
Produto de Números Complexos na Forma Polar
Dados os números complexos em sua forma polar:\begin{equation*}
z_1 = \rho_1 \left(\cos(\theta_1) + i~ \text{sen}(\theta_1)\right)\\
z_2 = \rho_2 \left(\cos(\theta_2) + i~\text{sen}(\theta_2) \right)
\end{equation*}
O produto entre $z_1$ e $z_2$ é dado por:
\begin{equation*}
z_1 \cdot z_2 = \rho_1 \left(\cos(\theta_1) + i~\text{sen}(\theta_1)\right) \cdot \rho_2 \left(\cos(\theta_2) + i~\text{sen}(\theta_2) \right)\\
z_1 \cdot z_2 = \rho_1 \rho_2 \left[\cos(\theta_1)\cos(\theta_2) + i~\cos(\theta_1)\text{sen}(\theta_2) + i~\text{sen}(\theta_1) \cos(\theta_2) + i^2~\text{sen}(\theta_1) \text{sen}(\theta_2)\right]\\
z_1 \cdot z_2 = \rho_1 \rho_2 [(\cos(\theta_1)\cos(\theta_2)-\text{sen}(\theta_1)\text{sen}(\theta_2)\\ + i~(\cos(\theta_1)\text{sen}(\theta_2)+\text{sen}(\theta_1)\cos(\theta_2))]
\end{equation*}
Sabemos que:
\begin{equation*}
\cos(\theta_1)\cos(\theta_2)-\text{sen}(\theta_1)\text{sen}(\theta_2) = \cos(\theta_1 + \theta_2)
\end{equation*}
e
\begin{equation*}
\text{sen}(\theta_1)\cos(\theta_2)+\text{sen}(\theta_2)\cos(\theta_1) = \text{sen}(\theta_1 + \theta_2)
\end{equation*}
Assim:
\begin{equation*}
z_1\cdot z_2 = \rho_1 \rho_2[\cos(\theta_1+\theta_2) + i~\text{sen}(\theta_1 + \theta_2)]
\end{equation*}
Por indução temos que:
\begin{equation*}
z_1 \cdot z_2 \cdot ~\cdots ~\cdot z_n =\\ \rho_1\rho_2 \cdots \rho_n[\cos(\theta_1+\theta_2+\cdots + \theta_n) + i~\text{sen}(\theta_1+\theta+2+\cdots+ \theta_n)]
\end{equation*}
Divisão de Números Complexos na Forma Polar
Dados os números complexos em sua forma polar:\begin{equation*}
z_1 = \rho_1 (\cos(\theta_1) + i~\text{sen}(\theta_1))\\
z_2 = \rho_2 (\cos(\theta_2) + i~\text{sen}(\theta_2))
\end{equation*}
A divisão entre $z_1$ e $z_2$ é dada por:
\begin{equation*}
\frac{z_1}{z_2} = \frac{\rho_1 (\cos(\theta_1) + i~\text{sen}(\theta_1))}{\rho_2 (\cos(\theta_2) + i~\text{sen}(\theta_2))} \cdot \frac{\rho_2 (\cos(\theta_2) - i~\text{sen}(\theta_2))}{\rho_2 (\cos(\theta_2) - i~\text{sen}(\theta_2))}
\end{equation*}
Vamos fazer, separadamente, as multiplicações do numerador e denominador da equação (1):
Numerador:
\begin{equation*}
\bullet ~\rho_1(\cos(\theta_1)+i~\text{sen}(\theta_1)) \cdot (\cos(\theta_2) -i~\text{sen}(\theta_2))=\\
= \rho_1(\cos(\theta_1)\cos(\theta_2) - i~\cos(\theta_1) \text{sen}(\theta_2) +\\+ i~\text{sen}(\theta_1)\cos(\theta_2) - i^2~\text{sen}(\theta_1)\text{sen}(\theta_2))\\
=\rho_1[(\cos(\theta_1)\cos(\theta_2) + \text{sen}(\theta_1)\text{sen}(\theta_2)) + \\+i~(\text{sen}(\theta_1)\cos(\theta_2) - \text{sen}(\theta_2)\cos(\theta_1))]\\
=\rho_1[\cos(\theta_1-\theta_2) + i~\text{sen}(\theta_1 - \theta_2)]
\end{equation*}
Denominador:
\begin{equation*}
\bullet ~\rho_2(\cos(\theta_2) + i~\text{sen}(\theta_2))(\cos(\theta_2)-i~\text{sen}(\theta_2))=\\
=\rho_2 (\cos^2(\theta_2) - i~\cos(\theta_2)\text{sen}(\theta_2) +\\+ i~\cos(\theta_2)\text{sen}(\theta_2) - i^2~\text{sen}^2(\theta_2))\\
= \rho_2(\cos^2(\theta_2)+\text{sen}^2(\theta_2))\\
=\rho_2(1)=\rho_2
\end{equation*}
Substituindo os valores do numerador e do denominador na divisão original obtemos:
\begin{equation*}
\frac{z_1}{z_2} = \frac{\rho_1 (\cos(\theta_1) + i~\text{sen}(\theta_1))}{\rho_2 (\cos(\theta_2) + i~\text{sen}(\theta_2))} \cdot \frac{\rho_2 (\cos(\theta_2) - i~\text{sen}(\theta_2))}{\rho_2 (\cos(\theta_2) - i~\text{sen}(\theta_2))}\\
\frac{z_1}{z_2} = \frac{\rho_1[\cos(\theta_1-\theta_2) + i~\text{sen}(\theta_1 - \theta_2)]}{\rho_2}\\
\frac{z_1}{z_2} = \frac{\rho_1}{\rho_2} [\cos(\theta_1-\theta_2) + i~\text{sen}(\theta_1 - \theta_2)]
\end{equation*}
Potenciação de Números Complexos na Forma Polar - (Primeira Fórmula de De Moivre)
Dado um número complexo não-nulo em sua forma polar $z=\rho [\cos(\theta) + i~\text{sen}(\theta)]$ e um número $n \in \mathbb{N}$ . A n-ésima potência de $z$ será dada por:\begin{equation*}
z^n = \rho^n[\cos(n\theta) + i~\text{sen}(n\theta)]
\end{equation*}
Para maiores detalhes consulte a demonstração da Primeira Fórmula de De Moivre.
Radiciação de Números Complexos na Forma Polar - (Segunda Fórmula de De Moivre)
Dado um número complexo não-nulo em sua forma polar $z=\rho [\cos(\theta) + i~\text{sen}(\theta)]$. A n-ésima raiz de $z$ será dada por:\begin{equation*}
z_w = \sqrt[n]{\rho}\left[ \cos\left( \frac{\theta+2k\pi}{n}\right) + i~\text{sen}\left(\frac{\theta + 2k\pi}{n}\right)\right]
\end{equation*}
Para maiores detalhes consulte a demonstração da Segunda Fórmula de De Moivre.
Veja mais:
Demonstração da 1ª Fórmula de De Moivre
Demonstração da 2ª Fórmula de De Moivre
Aplicação da 2ª Fórmula de De Moivre
Relação Trigonométrica Fundamental
Adição e Subtração de Arcos




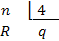




Olá amigo Kleber,
ResponderExcluirmeu caro vc pode enviar a questão de Física para o meu e-mail, e vou analisá-la. Não lhe garanto nada, mas posso tentar!
faltou na forma exponencial
ResponderExcluirno diagrama dos conjuntos numéricos há um espaço para números que não são naturais, não são racionais, não são irracionais, mas estão dentro do conjunto dos reais. Quem seriam estes números?
ResponderExcluirops, tb não são inteiros
ResponderExcluirNo trecho "Forma Trigonométrica ou Polar dos Números Complexos" começa uma série de erros, ou eu não estou entendendo a ideia ?
ResponderExcluirOlá Fábio. Tem alguns erros de digitação. Vou providenciar as correções. Obrigado pro avisar.
ExcluirUffa, obrigado ! Pensei que estava completamente boiando !
ResponderExcluirEstou aprendendo mto com o conteúdo de seu blog, muito obrigado mesmo !