Ultrapassando os Limites da Computação Pessoal... Quão Longe Podemos Ir?
Por Alexander J. Yee & Shigeru Kondo
Em 02 de agosto de 2010, foi completado o cálculo de π em 5.000.000.000.000 de casas decimais em um único computar e em tempo recorde.
Este cálculo traz mais 230.000.000.0000 a mais do que o recorde anterior por Fabrice Bellard, em dezembro de 2009.
O cálculo atual foi feito usando um programa criado por Alexander Yee e um computador desktop construído por Shigeru Kondo.
Veja uma pequena parte dos números calculados:
3,
1415926535 8979323846 2643383279 5028841971 6939937510 : 50
5820974944 5923078164 0628620899 8628034825 3421170679 : 100
4610126483 6999892256 9596881592 0560010165 5256375678 : 10,000
6683008238 3404656475 8804051380 8016336388 7421637140 : 12,000
1173213138 9574706208 8474802365 3710311508 9842799275 : 15,000
2968106203 7765788371 6690910941 8074487814 0490755178 : 20,000
8353013617 8653673760 6421667781 3773995100 6589528877 : 25,000
5091576463 9074693619 8815078146 8526213325 2473837651 : 40,000
0652623405 3394391421 1127181069 1052290024 6574236041 : 50,000
1716133957 5779076637 0764569570 2597388004 3841580589 : 75,000
7015078933 7728658035 7127909137 6742080565 5493624646 : 100,000
6136953089 9547584883 0242619627 5898594151 3780515805 : 120,000
8500384293 8167759796 1912729990 4591343960 4283622782 : 150,000
0400704911 1330970230 4687661585 7483135080 1444759928 : 200,000
5140252095 1792646811 5682982031 3618827396 4266233216 : 250,000
4956017828 2456727368 5631218502 0980470362 4641761986 : 400,000
4953622322 2219746596 1933252907 4042487602 5138195242 : 500,000
8761414451 9713784817 6211789772 4143554673 5467024250 : 750,000
5678796130 3311646283 9963464604 2209010610 5779458151 : 1,000,000
8653704276 8589418353 8706624969 4535897512 9763649216 : 1,200,000
7293649500 4049671124 7947151173 1960773799 1914462295 : 1,500,000
2907174473 5892565046 1663735632 3687106519 1457297909 : 2,000,000
0962872052 7420345883 0294305194 4240317833 1476913570 : 2,500,000
6667851395 4724032259 8065882978 5967469747 3349203390 : 4,000,000
4886585519 1846702365 4217617835 0518172132 0764619715 : 5,000,000
5377913223 9928659517 0653604450 1005321525 5014054157 : 7,500,000
2976735807 0882130902 2460461146 5810642210 6680122702 : 1,000,000,000,000
5296320811 9703828272 7315356530 7867141740 4641807691 : 1,200,000,000,000
9649292043 0823196832 7127227140 6977745121 1028636395 : 1,500,000,000,000
8386341797 9368318191 5708299469 1313121384 3887908330 : 2,000,000,000,000
7023378492 4587524911 1838622539 0987058051 8718886518 : 2,500,000,000,000
3638467628 3610607856 5071920145 5255995193 8577295739 : 4,000,000,000,000
6399906735 0873400641 7497120374 4023826421 9484283852 : 5,000,000,000,000
Abaixo segue um screnshot do programa utilizado com a validação concluída. O cálculo foi feito em várias etapas e não há uma única tela que mostre todo o cálculo do início ao fim.
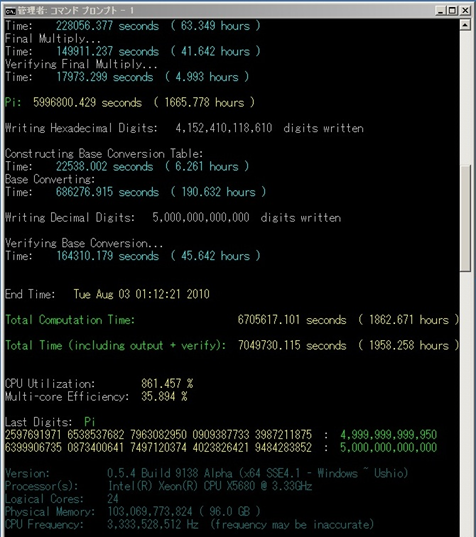 [Clique na imagem para ver em tamanho original]
[Clique na imagem para ver em tamanho original]
O cálculo principal foi de 90 dias no ambiente de trabalho sugerido por Kondo. Durante a computação um erro foi detectado e corrigido via software e os resultado finais não seriam afetados. O erro de cálculo acredita-se ser causado por uma anomalia de hardware ou simplesmente uma instabilidade do hardware.
Devido ao tamanho do cálculo, uma enorme quantidade de memória foi necessária: cerca de 22TB de disco foi necessária para realizar a computação; e outros 3,8TB de disco foram necessária para armazenar a saída de dígitos decimais e hexadecimais.
Se os dígitos fossem armazenados em um único arquivo descompactado texto em ASCII, o tamanho combinado dos dígitos decimais e hexadecimais seria de 8,32TB.
Todas as unidades usadas são binárias:
GB = 230 bytes
TB = 240 bytes
A Computação de Cálculo de π
Início: às 06h19 PM (JST) em 04 de maio de 2010
Fim: às 01h12 AM (JST) em 03 de agosto de 2010
Total de 90 dias de computação.
A Verificação do Cálculo
64 horas – Preliminar – BBP Bellard’s
66 horas – Secundário – BBP Plouffe
Veja cronologia detalhada aqui.
Objetivos
“Porque é PI... e porque nós podemos!”
Em uma nota mais séria Yee diz que após o anúncio de Fabrice Bellard 2,7 trilhões de dígitos em um trabalho “relativamente barato”, ficou bastante pessoal que o limite da computação pessoal era muito superior.
Yee e Kondo utilizaram um hardware mais poderoso, e por serem fanáticos por hardwares, tiveram à disposição máquinas poderosas e, então, decidiram ver o quão longe poderiam ir utilizando os limites da computação pessoal.
O principal desafio para um calcula de tal porte é que software e hardware são levados para além dos seus limites.
Para um cálculo tão longo, o fracasso não é apenas uma probabilidade. É um dado adquirido, pois existem demasiados componentes que podem falhar. Assim surgem as perguntas:
1) Quanto pode um hardware ser expandido, mantendo um nível aceitável de confiabilidade?
2) É possível construir um software com suficiente tolerância a falhas para cobrir as falhas de hardware?
Hardware Utilizado
O computador utilizado tinha as seguintes configurações:
Processador:
2 X Intel Xeon X5680 @ 3.3 GHz – (12 núcleos físicos – 24 hiperprocessamento)
Memória:
96 GB DDR3 @ 1066MHz – (12 X 8 GB – 6 canais) – Samsung (M393B1K70BH1)
Placa mãe:
Asus Z8PE-D12
Discos Rígidos:
1 TB SATA II (Boot drive) – Hitashi (HDS721010CLA332)
3 X 2 TB SATA II(Armazenamento de saída de PI) – Seagate (ST32000542AS)
16 X 2TB SATA II (Computação) – Seagate (ST32000641AS)
Raid Controller:
2 X LSI SAS MegaRAID 9260-8i
Sistema Operacional:
Windows Server 2008 R2 Enterprise X64
Operado por:
Shigeru Kendo
Fotos do Hardware Utilizado
As Fórmulas Utilizadas no Cálculo
Para o cálculo principal, foi utilizada a fórmula de Chudnovsky:
Para a verificação foi utilizada as seguintes fórmulas BBP:
Fórmula de Plouffe:
Fórmula de Bellard:
A fórmula de Chudnovsky foi utilizada para calcular 4.152.410.118.610 dígitos hexadecimais de π. Para verificar a exatidão dos dígitos, as fórmulas BBP forma utilizadas para calcular diretamente os dígitos hexadecimais em várias posições, incluindo a 4.152.410.118.610ª posição.
Uma conversão radix foi feita para conversão dos dígitos de base 16 para base 10, produzindo 5 trilhões de casas decimais!
Verificação de Dígitos Decimais
Após a conversão radix, π ficou disponível em base 10 e foram feitas as seguintes verificações:
Computação usando aritmética de base 10:
Computação usando aritmética binária:
Se A = B , há a “probabilidade muito alta” da conversão estar correta.
Há muito mais a ser visto. Acessem o site:
Number World
Veja Mais:
Uma Breve Cronologia de PI
A História do Símbolo do Infinito




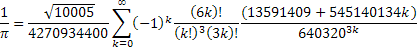
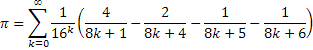
![clip_image002[9] clip_image002[9]](http://lh5.ggpht.com/_Qmjqb2Gk9no/TPvB-iGnv-I/AAAAAAAAK74/UslpVgobaZ0/clip_image002%5B9%5D_thumb.gif?imgmax=800)
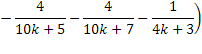

∏ = x/y x=∏y logo x=∞ e y = ∞/x então ∏=∞
ResponderExcluirem 2013 foi feito um caculo que mostrou pi com 8.000.000.000.000.000 casa decimais ( nao sei nem falar este nomero
ResponderExcluirmeu deus nunca vi mentira maior que essa, vocês não veem que nunca vão chegar em um resultado, o pi é um número infinito seus bestas, e o máximo que chegaram até hoje é de 2,5 bilhões se não me falha a memória..... vocês deveriam pensar bem antes de colocar uma mentira tão grande como essa e se passarem por burros e idiotas na internet outra vez!
ResponderExcluirmisericórdia! é o fim do mundo mesmo meu deus!
Os dados são de 2010, e na época Shigeru Kondo calculou 5 trilhões de dígitos. Em setembro de 2016, o cálculo chegou a 12 trilhões.
Excluirhttp://www.numberworld.org/misc_runs/pi-12t/
https://en.wikipedia.org/wiki/Chronology_of_computation_of_%CF%80#cite_note-39
O fato de você vir aqui destilar a sua ignorância só me faz crer que quem é burro(a) é você, pois não se dá ao trabalho de fazer uma simples pesquisa no google. Experimente, não dói!
O que se encontra nestes cálculos são aproximações. Não vou gastar meu tempo com você tentando te explicar como calcular aproximações de pi. Pesquise se quiser.
Procure ser mais gentil em seus comentário para que haja uma discussão construtiva.
Parabéns Kleber, falou tudo.
ExcluirQuanta ignorância, em vez de buscar conhecimento para saber o que falar, se sente inseguro e com medo do que pode vir e fala asneiras.
ExcluirOlá. Saberia me informar onde posso baixar um arquivo confiavel com os primeiros 2 milhões de dígitos ou mais?
ResponderExcluirobg
ResponderExcluirMuito bom.
ResponderExcluir