 Certamente não era nada confortável uma viagem de Londres a Edimburgo no distante ano de 1615. Em veículos puxados a cavalos, por estradas esburacadas e poeirentas, o percurso parecia interminável. Mas para o eminente professor Henry Briggs (1556 – 1630), que ocupava no Gresham College de Londres a primeira cátedra de matemática criada na Inglaterra, valia a pena o sacrifício. Afinal, ia conhecer John Napier (1550 – 1617), que no ano anterior tornara pública uma invenção sua que sacudiria a matemática da época: os logaritmos.
Certamente não era nada confortável uma viagem de Londres a Edimburgo no distante ano de 1615. Em veículos puxados a cavalos, por estradas esburacadas e poeirentas, o percurso parecia interminável. Mas para o eminente professor Henry Briggs (1556 – 1630), que ocupava no Gresham College de Londres a primeira cátedra de matemática criada na Inglaterra, valia a pena o sacrifício. Afinal, ia conhecer John Napier (1550 – 1617), que no ano anterior tornara pública uma invenção sua que sacudiria a matemática da época: os logaritmos.
O nobre escocês John Napier, Barão de Murchiston, ao contrário de Briggs, não era um matemático profissional. Além de administrar suas grandes propriedades, dedicava-se a escever sobre vários assuntos. Às vezes sem conseguir se livrar dos preconceitos da época, como num trabalho de 1593 em que procurava mostrar que o papa era o anticristo e que o Criador pretendia dar fim ao mundo entre 1688 e 1700. Às vezes como um visionário iluminado, como quando previu os submarinos e os tanques de guerra, por exemplo. Às vezes com a ponderação de um autêntico cientista, como no caso dos logaritmos, em cuja criação trabalhou cerca de 2º anos.
O termo logaritmo foi criado por Napier: de logos e arithmos, que significavam, respectivamente, “razão” e “número”. E a obra em que, no ano de 1614, apresentou essa sua descoberta recebeu o título de Mirifice logarithmorum canonis descriptio (ou seja, Uma descrição da maravilhosa regra dos logaritmos). Nela Napier explica a natureza dos logaritmos, segundo sua concepção, e fornece uma tábua de logaritmos dos senos de 0° a 90°, de minuto em minuto. A razão de aplicar sua idéia à trigonometria se deveu ao fato que o objetivo principal dessa tábua era facilitar os longos e penosos cálculos que navegadores e astrônomos enfrentavam diuturnamente.
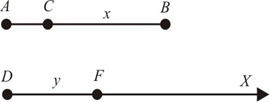
Em linguagem moderna, Napier concebeu os logaritmos da seguinte maneira: Imaginemos os pontos C e F percorrendo respectivamente o segmento AB e a semi-reta DX, partindo ao mesmo tempo de A e D, com a mesma velocidade inicial; admitamos, ainda, que, numericamente, a velocidade de C seja dada em função de CB e que a velocidade de F seja constante; nessas condições Napier definiu como logaritmo de x = CB o número y = DF. Assim, explicitamente, nesse conceito não intervém a idéia de base. Mas pode-se provar que:
A potência de 107 surge aí porque Napier considerava que AB = 107. Aliás, à época de Napier o seno não era definido como hoje, por meio de uma razão; era a medida da semicorda do ângulo central, tomando como unidade um submúltiplo do raio da circunferência considerada. E, para evitar frações, um submúltiplo muito pequeno – no caso 1/107 do raio.
Napier também estava ansioso por conhecer Briggs, a ponto de se decepcionar com o atraso de sua chegada, achando que não viria. Consta que ao se verem ficaram vários minutos sem conseguirem articular nenhuma palavra. Durante o mês que Briggs passou em Edimburgo, certamente o assunto dominante de suas conversas com Napier foram os logaritmos. E acabaram concordando que uma tábua de logaritmos de base 10 seria mais útil. Mas Napier não viveria para levar a termo esse trabalho – Briggs e outros o fariam.
Considerando as prioridades da época, Briggs e Napier acertaram nessa opção. Mas, com o advento das calculadoras manuais e dos computadores, as tábuas de logaritmos perderam sua utilidade. Hoje, o que importa especialmente são certas propriedades funcionais da função logaritmo e de sua inversa, a função exponencial. E nesse sentido deve-se privilegiar, isto sim, a base e = 2,7182...
Texto de: Hygino H. Domingues
Veja Mais:
Utilizando Tábuas para Calcular Logaritmos
Utilizando Tábuas para Encontrar Aproximações de Raízes
Utilizando Tábuas para Encontrar Aproximações de Expressões Complexas



essa pagina é otima para estudantes!!
ResponderExcluire para sabermos mais sobre a informatica
amei essa pagina ela é muito boa
ResponderExcluirfiz um trabalho e tirei 10 obrigada!
poor:rafaell ravi queiroga
gostei muito sou um cara super intelingente
ResponderExcluire adororo paginas que me mostrem algo novo
sou um ricasso de fortaleza bjss lucas silva
Obrigado pelos comentários.
ResponderExcluir