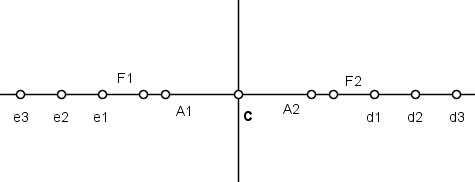
Vamos construir uma hipérbole a partir de seus vértices e de seus focos. Sejam dados o eixo real contendo os focos F1 e F2, os vértices A1 e A2 e o centro C:
Para o ramo da esquerda, com a ponta seca do compasso em F1 e raio qualquer menor que F1C, marque o ponto e1 e com mesma abertura com a ponta seca em e1, marque e2 e do mesmo modo marque e3. Para o ramo da direita proceda da mesma forma, sendo F2d1 = F1e1.
Com centro em F1 e abertura igual a A1e1, A1e2 A1e3, descreva os arcos indicados em verde; Para o ramo da direita, proceda da mesma forma com centro em F2:
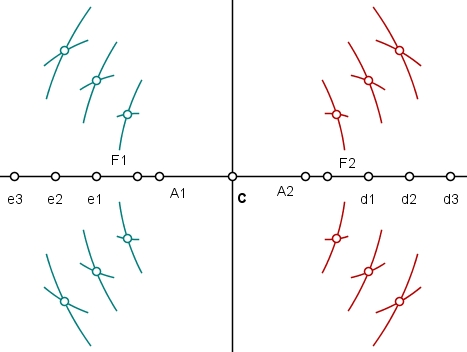
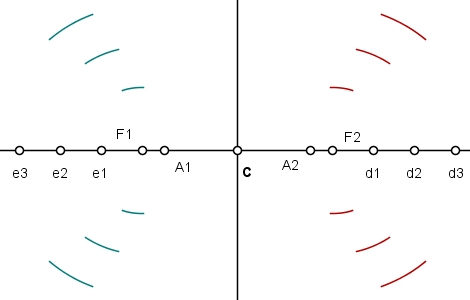 Agora, com a ponta seca do compasso em F1 e abertura igual a A1d1, A1d2 e A1d3, descreva arcos interceptando os arcos traçados na etapa anterior; Com centro em F2, proceda da mesma forma:
Agora, com a ponta seca do compasso em F1 e abertura igual a A1d1, A1d2 e A1d3, descreva arcos interceptando os arcos traçados na etapa anterior; Com centro em F2, proceda da mesma forma:
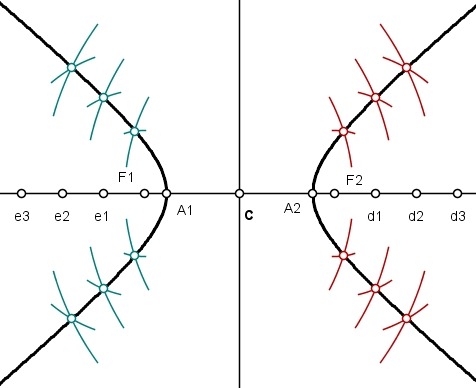
Por estes pontos de intersecção e pelos vértices A1 e A2, passam os ramos da hipérbole:
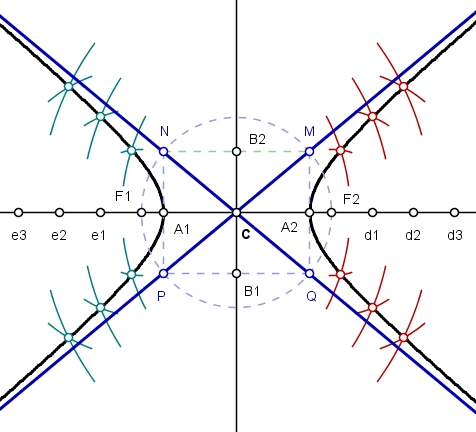
Para encontrarmos as assíntotas, descrevendo uma circunferência centrada em C e raio CF1. Trace perpendiculares ao eixo real passando pelos vértices A1 e A2. Os pontos de intersecção com circunferências definem o quadrilátero MNPQ. As assíntotas sãos os prolongamentos das diagonais desse quadrilátero:
Vejam os ramos da hipérbole em preto e as assíntotas em azul.
Veja mais:
A Equação da Hipérbole
Construções Geométricas de Tangentes com Régua e Compasso (Parte 1)
Construções Geométricas de Tangentes com Régua e Compasso (Parte 2)




Olá Kleber,
ResponderExcluirGostei bastante desse método de construção da hipérbole, complementado seu artigo anterior sobre sua equação.
Acompanho seu blog há algum tempo e sempre vejo ótimos artigos por aqui.
Saudações.
Prof. Alexandre
Muito bom o seu post. Agora como fazer se as assíntotas já são dadas? Por exemplo, se já se sabe o valor de b?
ResponderExcluirAbraços.
Olá. Eu já havia tentado isso também, quando estava fazendo um estudo sobre trissecção de ângulo utilizando uma hipérbole. Na época não tinha conseguido e acabei deixando pra trás. Vou ver se consigo alguma coisa.
ExcluirAbraços.
Encontrei algo que ajudou bastante: http://www.professores.uff.br/kowada/ga/ead/ga1V1aula21.pdf
ExcluirObrigado pela atenção.
Abraços
É exatamente para esse problema, a solução dada por Papus de Alexandria. Interessante, não é mesmo?
ResponderExcluirObrigado pelo material, vou estudá-lo.
ResponderExcluirAbraços!
Muito bom da mesma forma que minha professora me ensinou. Passei aqui pra relembrar.
ResponderExcluirCaro amigo seu blog é muito claro e fácil de compreender confesso que agora sim estou entendendo bem hipérbole. Mas, gostaria de saber se poderia me ajudar nessas questão:
ResponderExcluirENCONTRE UMA EQUAÇÃO DE UMA HIPERBOLE EQUILATERA QUE PASSA PELOS PONTO P(2,3) TEM FOCOS NO EIXO Y E CENTRO NA ORIGEM DO SISTEMA CARTESIANO.
A minha filha estava precisando, excelente explicação 👏👏
ResponderExcluir