Os trabalhos de Arquimedes são obras-primas de exposição matemática. Além de exibirem grande originalidade, habilidade computacional e rigor nas demonstrações, são escritos numa linguagem altamente acabada e objetiva. Cerca de dez tratados de Arquimedes se preservaram até nossos dias e há vestígios de outros extraviados. Veja aqui a lista das obras de Arquimedes que, depois de muitas vicissitudes, chegaram à nós, seguindo a ordem da edição crítica de Heiberg.
Onde r é o raio e k é uma constante de proporcionalidade. Podemos definir a espiral como o lugar dos pontos P que se movem uniformemente ao longo de um raio que, por sua vez, gira uniformemente numa plano em torno da origem.
Vamos aqui construir a espiral de Arquimedes utilizando apenas régua e compasso.
O processo de construção consiste em dividir uma circunferência em n partes iguais, dividir o raio em n partes iguais e descrever circunferências concêntricas com raios iguais à distância da origem O às divisões do raio. Em seguida, marcar os pontos Pn nas intersecções dos raios rn com as circunferências cn. A curva que passa por esses pontos é a espiral de Arquimedes. Vejamos passo-a-passo:
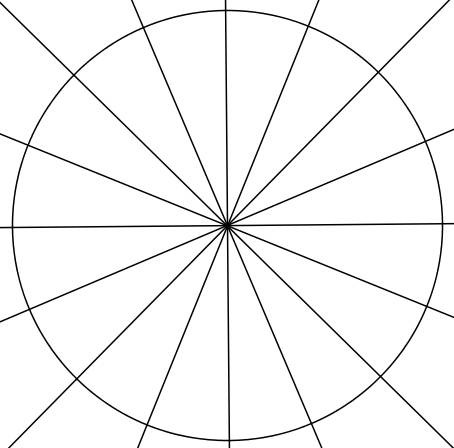
1) Descreva uma circunferência e divida-a em n partes iguais. Vamos utiliza n = 16 por ser de fácil obtenção, somente traçando as mediatrizes:
2) Agora vamos dividir o raio em n = 16 partes iguais. Já vimos aqui como dividir um segmento de reta em n partes:
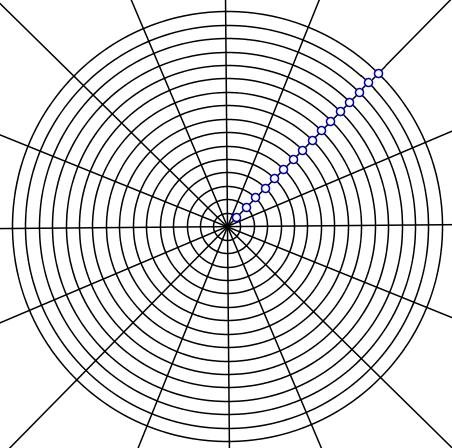
3) E tracemos as circunferências concêntricas passando pelos pontos da divisão do raio:
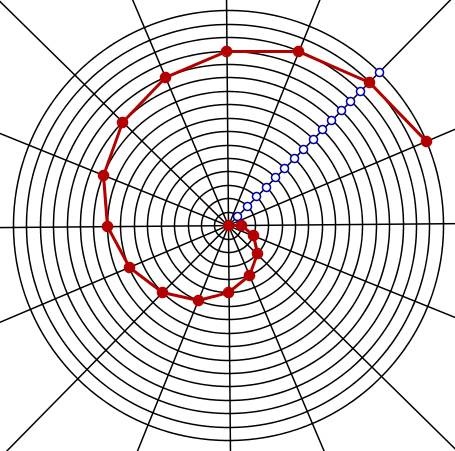
4) Marcamos os pontos P nas intersecções das circunferências cn com os raios rn e unimos esses pontos com segmentos de retas:
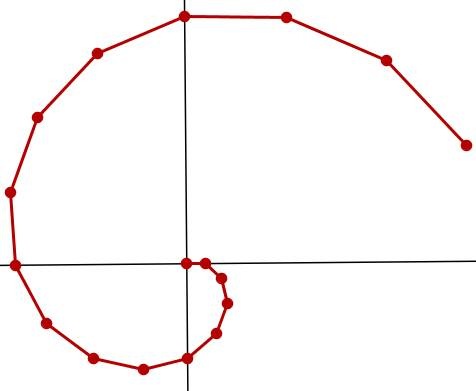
5) A curva que passa por esses pontos é a espiral de Arquimedes:
Referências:
[1] Introdução à História da Matemática – Howard Eves
Veja mais:
Construção Geométrica da Parábola com Régua e Compasso
Construção Geométrica da Hipérbole com Régua e Compasso
Construção Geométrica da Elipse com Régua e Compasso (Parte 1)
Construção Geométrica da Elipse com Régua e Compasso (Parte 2)
Estava esses dias estudando alguns assuntos da obra de Arquimedes e me deparei com esta curva que também pode ser usada para a quadratura do círculo. Parabéns pelo post!
ResponderExcluirObrigado Paulo. Além disso também é possível trisseccionar ângulos! Incrível não é como Arquimedes era inteligente! Vou estudar um pouco mais sobre esse assunto e quem sabe consigo um bom artigo.
ResponderExcluirObrigado e um abraço.
Espetacular!
ResponderExcluirMuito bom o post.
ResponderExcluirTenho muitas construções geométricas desde a época que cursava faculdade, uma delas é a construção de espirais policentrais usando régua e compasso. Quem sabe consigo reproduzi-las no Geogebra e publicar alguns desenhos. Me senti inspirado, vamos ver se o tempo deixa.
Abraço!
Uma pena nã oensinarem mais desenho geométrico no ensino fundamental. Faz uma diferença enorme no aprendizado.
ResponderExcluirObrigado pelos comentários!
Olá Kleber,
ResponderExcluirDe fato trabalho Desenho Geométrico no Ensino Fundamental de uma escola particular. Quando construímos a Espiral de Arquimedes os alunos ficam fascinados por esse tema.
Abs.
Carlos Roberto
Diadematematica