A massa (m) de um corpo é a medida da quantidade de matéria nele existente; já o volume (V) é a medida do espaço por ele ocupado. Se a massa por unidade de volume for constante através de todo o corpo, este corpo é homogêneo ou tem massa específica constante.
Em Física é desejável considerar uma dada massa concentrada em um único ponto, denominado centro de gravidade. Se um corpo é homogêneo, esse ponto coincide com o centro geométrico. Por exemplo, o centro de gravidade de um círculo é o centro deste círculo. Isso é fácil de imaginar: posicione a ponta seca do compasso em uma folha de papel e descreva uma circunferência. Assim, o centro O onde foi posicionada a ponta seca do compasso é o centro de gravidade do círculo formado.
O centro de uma folha de papel retangular se encontra entre as duas faces, porém consideramos como existindo em uma das faces, na intersecção de suas diagonais. Assim, o centro de gravidade de uma folha de pequena espessura coincide com o centro geométrico da folha considerada como uma área plana.
O momento (ML) de uma área plana em relação a um eixo L é o produto da área A pela distância de seu centro de gravidade ao eixo. O momento de uma área composta em relação a um eixo é a soma dos momentos das áreas componentes em relação ao eixo.
Para determinarmos o momento de uma área plana em relação a um eixo coordenado é útil fazer um esboço da área em questão. Assim podemos utilizar o conceito do retângulo elementar, que tem largura infinitesimal. Formamos, então, o produto da área do retângulo pela distância do seu centro de gravidade ao eixo. Em seguida, fazemos a soma para todos os retângulos, aplicando a integral definida.
Para uma área plana A, tendo seu centro de gravidade em e momentos denotados por Mx e My em relação aos eixos dos x e y serão dados por:
Exemplo 1: Para exemplificar e nos acostumar com o método, vamos determinar os momentos e as coordenadas do centro de gravidade da figura abaixo.
Com a geometria desta figura é simples, podemos dividi-las em vários retângulos, cujos centros de gravidade são denotados por: A, B. C e D.
Vejam que o retângulo superior (A) tem uma área A igual a 10 unidades de área (u.a.):
E o centro de gravidade será:
Vejam que a coordenada x é exatamente a metade do comprimento do retângulo e a coordenada y é a metade de sua altura. Mas para a altura, fazemos:
Para o retângulo (B), temos que:
Para o retângulo (C), temos que:
E para o retângulo (D), temos:
A área total da figura é:
Podemos agora calcular os momentos dos retângulos em relação ao eixo dos x, fazendo o produto entre a área e a distância ao eixo dos x:
Assim, o momento da área da figura em relação ao eixo dos x é a soma dos momentos dos retângulos individuais:
E analogamente, o momento da área da figura em relação ao eixo dos y é:
Logo, temos que:
Assim, o ponto de coordenadas igual a (67/34 ; 5) é o centro de gravidade da figura.
Exemplo 2: Achar os momentos em relação aos eixos coordenados da área plana limitada no 2º quadrante pela curva x = y2 – 9.
Aqui vamos introduzir o conceito do retângulo elementar, que é um retângulo de largura infinitesimal. Considere o esboço do gráfico:
Observando o retângulo elementar da figura acima, podemos ver que sua área é igual a e seu centro de gravidade é dado por
. Logo, seu momento em relação ao eixo dos x é
. Então:
Da mesma forma podemos determinar o momento do retângulo elementar em relação ao eixo dos y, que é igual a . Então:
Exemplo 3: Achar o centro de gravidade da área limitada no primeiro quadrante pela parábola y = 4 – x 2.
O centro de gravidade do retângulo elementar é (x ; 1/2y).
A área sob a curva no primeiro quadrante será dada pela soma dos retângulos elementares:
Os momentos Mx e My serão dados por:
e
Para o cálculo das coordenadas do centro de gravidade, fazemos:
e
Logo, as coordenadas do centro de gravidade da área limitada pela parábola no primeiro quadrante da curva são (3/4 ; 8/5).
Exemplo 4: Achar o centro de gravidade da área sob a curva y = 2sen (3x), desde x = 0 à x = π/3.
Fazendo uso do retângulo elementar, cujo centro de gravidade é igual a (x ; 1/2y), temos que:
Para o cálculo das coordenadas do centro de gravidade, fazemos:
e
Logo, as coordenadas do centro de gravidade da área limitada pela parábola no primeiro quadrante da curva são (π/6 ; π/4).
Referências:
[1] Cálculo Diferencial e Integral – Frank Ayres Jr. – McGraw-Hill
Veja mais:
O Cálculo Integral
Volume de uma Calota Esférica
Volume de um Segmento Esférico
Teste da Integral para Convergência de Séries
















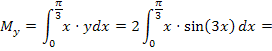


É por isso que li que Newton usou integral para dizer que a força G atua no centro das esferas. É interessante que naquela época foi uma ferramenta que ele próprio inventou...
ResponderExcluirNewton foi um cientista à frente de seu tempo. Realmente foi incrível suas descobertas, e hoje fazemos uso de muitas delas sem mesmo saber o quanto de energia foi desprendida a partir de uma ideia. Quanto mais eu estudo sobre Newton, maior é minha admiração.
ResponderExcluirAbraços amigo.
Boa tarde Kleber Kilhian!
ResponderExcluirQuero, antes de tudo, te dar parabéns pelo seu blog "baricentro da mente". Venho consultando ele para estudos particulares. As demonstrações são claras e objetivas. Se me permite, tenho uma curiosidade quanto a sua pessoa. Gostaria de saber o que você estudou e faz atualmente. É somente uma curiosidade, nada demais. Se puder me responder ficarei agradecido. No mais, desejo sorte na sua vida e saúde para você e sua família. abraços.
Perdoe kleber. Esqueci de colocar meu nome no comentário acima. Meu é Fernando.
ResponderExcluirOlá Fernando. Obrigado pelos elogios.
ResponderExcluirSou licenciado em Matemática pela faculdade UNIFIG em Guarulhos. No entanto, não leciono. Sou Técnico em Eletrônica há 18 anos e trabalho no ramo e atualmente estou numa empresa de tecnologia onde desenvolvemos computadores de bordo customizados, rastreadores, velocímetro digitais, entre outros. Em minhas horas vagas me dedico à minha família, e quando posso, estudo um pouco sobre os artigos aqui publicados.
Fico satisfeito em saber que meu trabalho está ajudando outras pessoas.
Fique a vontade em perguntar e volte sempre!
Abraços.
no exemplo 1: Não seria 76/34 = 38/17 ?
ResponderExcluirAssim, o ponto de coordenadas igual a (38/17 ; 5)?
Olá amigo. Sim, a resposta que dei só não foi simplificada. Assim a resposta que você deu está correta.
ExcluirObrigado pela visita. Volte sempre!
O QUE QUIS DIZER É QUE VC COLOCOU 67/34 E NAO 76/34 QUE SERIA O CORRETO..
ResponderExcluirOTIMA EXPLICAÇÃO..ME SALVOU NA PROVA DE RM ;)
VLW
SUGESTÃO: FAZER PASSO A PASSO DE UMA DIAGRAMA DE TENSÃO V,N,M
"A massa (m) de um corpo é a medida da quantidade de matéria nele existente"
ResponderExcluirEsse conceito está errado. Massa se divide em inercial e gravitacional, ambas medidas em kg no SI. Quantidade de matéria é uma grandeza fundamental medida em mol e pertence as sete fundamentais do SI.
Tem um erro no exemplo 3 na hora de calcular as coordenadas do centro de gravidade MY/A; MX/A o valor de A calculado a partir da integral deu 18/3 e vocês colocaram 16/3.
ResponderExcluirVerdade. Foi um erro de digitação. Em breve farei a correção.
ExcluirAbraços.