Que sentido tem falarmos em medir tempos da ordem de milhões de anos? Tem um sentido histórico referente ao passado, ou seja, podemos tentar determinar a idade de objetos ou materiais (época em que foram formados), ou a época no passado em que ocorreram eventos de interesse.
O principal método empregado para este fim é o da datação radioativa. A ideia básica do método é muito simples e pode ser compreendida pela seguinte analogia: se tivermos sobre uma chama uma chaleira com água e conhecermos a quantidade de água na chaleira no instante em que se inicia a ebulição, bem como a quantidade vaporizada por unidade de tempo, podemos determinar o tempo transcorrido desde o início da ebulição medindo a quantidade de água restante na chaleira.
Um “relógio natural” deste tipo são as substâncias radioativas. A radioatividade foi descoberta por acaso por Henri Becquerel em 1896, pela sensibilização de chapas fotográficas que haviam sido guardadas numa gaveta onde havia sais de urânio. Foi descoberto posteriormente que o urânio emite radiações que o fazem passar por uma série de transmutações radioativas (em elementos diferentes), até chegar a um elemento estável, o chumbo. Descobriu-se também a existência de um grande número de outros elementos radioativos.
O decréscimo com o tempo da quantidade restante de um elemento radioativo não é proporcional ao tempo transcorrido, como no exemplo da chaleira, mas obedece à assim chamada “lei exponencial” da desintegração radioativa. Para entendê-la, vamos de novo recorrer a uma analogia: consideremos um país hipotético onde a taxa de inflação é de 100% ao ano.
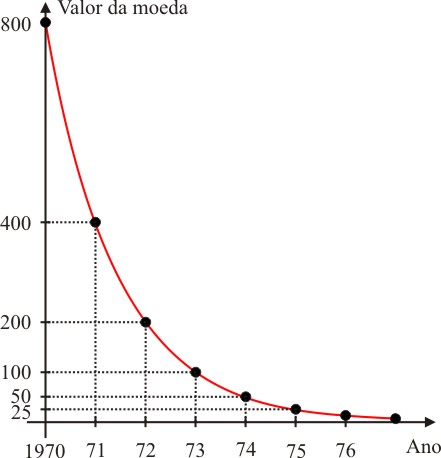 [Figura 1: Decaimento exponencial]
[Figura 1: Decaimento exponencial]
O gráfico acima mostra como evoluiria em função do tempo o valor aquisitivo de uma soma fixa dessa moeda, equivalente a 800 unidades no ano 1970. Ao fim de cada ano, o valor se terá reduzido à metade do valor no ano anterior. O valor após x anos será uma fração do valor inicial dada por:
$$
\frac{1}{\alpha} = \frac{\text{valor após }x \text{ anos}}{\text{valor inicial}}=\left( \frac{1}{2}\right)^x=\frac{1}{2^x}
$$
Se conhecermos o valor $\alpha$, podemos então determinar o tempo decorrido $x$, em anos, por:
$$
(x)_{anos} = \log _2 \alpha
$$
O tempo em que leva para se passar de um dado valor à metade desse valor, chama-se meia-vida. No exemplo acima, a meia-vida do poder aquisitivo da moeda é 1 ano.
O número N de átomos numa amostra de uma substância radioativa também obedece à lei exponencial de desintegração, com meias-vidas que podem variar desde frações de segundo até bilhões de anos, conforme a substância. Costuma-se designar por $T_{1/2}$ a meia-vida. Por exemplo, para $U^{238}$ (urânio 238), $T_{1/2} \approx 4,5 \times 10^9$ anos. Se $N_0$ é a população inicial de átomos radioativos (número inicial na atmosfera), após decorrido um tempo $t$, que corresponde a:
$$
x = \frac{1}{T_{1/2}} \quad \text{meias-vidas}
$$
a população se terá reduzido a uma fração:
$$
\frac{1}{\alpha} = \frac{N(t)}{N_0}
$$
do valor inicial, onde $N(t)$ é o número de átomos radioativos no instante $t$. Combinando as equações acima, obtemos o valor do tempo decorrido $t$:
$$
t = T_{1/2} \cdot \log _2 \left[ \frac{N(t)}{N_0} \right] \tag{1}
$$
Na aplicação de método de datação radioativa à medida de tempos muito remotos no passado, tem importância fundamental o fato de que os átomos radioativos são relógios de muita confiança, “a prova de choques”, porque as amostras analisadas terão sido submetidas a tremendas variações de pressão, temperatura e outras condições ambientais. A meia-vida da desintegração radioativa não é afetada por esses fatores, porque depende apenas de processos envolvendo forças de interação e energias nucleares, muito maiores do que as que estão associadas às flutuações do ambiente.
Datação pelo $K^{40}$
Um dos métodos mais empregados de datação geológica baseia-se nas propriedades de um isótopo radioativo do potássio, o $K^{40}$. O isótopo de ocorrência mais comum, que é estável, é o $K^{39}$, e a abundância relativa atual numa amostra de potássio é de 1 átomo de $K^{40}$ para cada 8.400 átomos de $K^{39}$.
A meia-vida do $K^{40}$ é:
$$
T_{1/2} = 1,3 \times 10^9 \quad \text{anos}
$$
Como sabemos disso? Não é esperando um bilhão de anos para ver uma população inicial reduzir-se a cerca da metade! A meia-vida de uma substância radioativa pode ser medida detectando as radiações por ela emitidas. O número de contagens do detector permite medir a fração dos átomos que se desintegram por segundo, determinando, assim, $T_{1/2}$. Para ima amostra macroscópica, em que a população de átomos radioativos pode ser da ordem de $10^{20}$ átomos, isto leva a um número de contagens por segundo facilmente detectável, mesmo para meias-vidas tão longas como a do $K^{40}$.
O $K^{40}$ se desintegra de duas maneiras diferentes, que mantêm proporções fixas entre si: 12% dos átomos de $K^{40}$ se desintegram em argônio $40 (A^{40})$ e os 88% restantes em cálcio $40 (Ca^{40})$. O argônio é um gás nobre, ou seja, quimicamente inerte (não se combina com outras substâncias), e fica preso nos interstícios do material que continha o $K^{40}$, de modo que é preservado após sua formação. Isto já não acontece com o cálcio, que forma vários outros compostos químicos.
Suponhamos, por exemplo, que a análise química de uma amostra de rocha de $1\ g$ revele a presença de $4,21 \times 10^{-2}\ g$ de potássio $(39+40)$ e $9,02 \times 10^{-7}\ g$ de argônio $(40)$. O cálcio não precisa ser analisado. Qual é a idade da amostra?
Podemos obter o número atual de átomos de cada elemento na amostra a partir das quantidades em gramas, lembrando que o número de átomos em $1 \text{mol}$ de $K$ e $A$ é o número de Avogadro:
$$6,02 \times 10^{23}\quad \text{átomos/mol}
$$
e que as massas atômicas são:
$$
K^{39} \quad \text{à} \quad 39,10\\
\ \\
A^{40} \quad \text{à} \quad 39,95
$$
Assim, $39,1\ g$ de $K^{39}$ equivalem a $6,02 \times 10^{23}$ átomos de $K^{39}$, e $39,95\ g$ de $A^{40}$ equivalem a $6,02 \times 10^{23}$ átomos de $A^{40}$.
Os dados acima revelam então que há atualmente na amostra $6,48 \times 10^{20}$ átomos de potássio e $1,36 \times 10^{16}$ átomos de argônio. Dada a abundância relativa de $K^{40}$, o número atual de átomos de $K^{40}$ é:
$$N(t) = \frac{6,48 \times 10^{20}}{8.400} = 7,71 \times 10^{16}\quad \text{átomos} \tag{2}
$$
Por outro lado, todos os átomos de $A^{40}$ na amostra provêm de desintegração do $K^{40}$, mas só se formam $12$ átomos de $A^{40}$ para cada $100$ desintegrações de $K^{40}$ (as restantes levam ao $Ca^{40})$. Logo, o número total de átomos de $K^{40}$ que se desintegram deve ser:
$$\frac{100}{12} \times 1,36 \times 10^{16} = 1,133 \times 10^{17}
$$
e a população inicial de $K^{40}$ na amostra era:
$$N_0 = 11,33 \times 10^{16} + 7,71 \times 10^{16} = 1,90 \times 10^{17} \tag{3}
$$
Substituindo os valores encontrados em $(2)$ e $(3)$ na equação $(1)$, obtemos:
$$t = T_{1/2} \cdot \log _2 \left[ \frac{N(t)}{N_0} \right]
$$
Onde a meia vida do $K^{40}$ = $T_{1/2} = 1,3 \times 10^9$ anos:
t = 1,3 \times 10^9 \cdot \log _2 \left[ \frac{1,90}{0,771} \right]\\
\ \\
t = 1,3 \times 10^9 \cdot \log _2 2,464\\
\ \\
t = 1,3 \times 10^9 \cdot \frac{\log 2,464}{\log 2}\\
\ \\
t = 1,3 \times 10^9 \times 1,30\\
\ \\
t = 1,69 \times 10^9 \quad \text{anos}
$$
Referências
- Física Básica, V.1, H. Moysés Nussenzveig




Postar um comentário