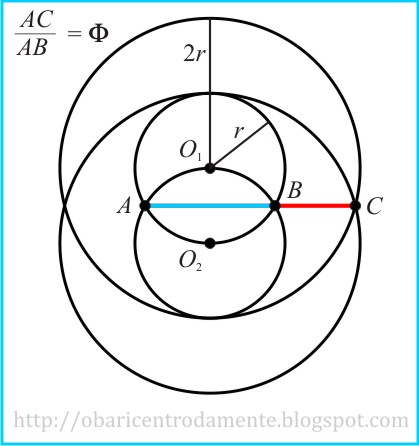
Esta é uma construção de com sobreposição de circunferências. Duas circunferências concêntricas de raios r e 2r sobrepõem-se a outras duas circunferências concêntricas idênticas, de tal modo que o centro das duas primeiras seja um ponto da circunferência menor da segunda. Unindo com um segmento de reta os pontos de intersecção entre as duas circunferências menores e prolongando-a até o ponto de intersecção das circunferências maiores, obtemos que a razão entre AC e AB é a razão áurea, obtendo PHI.
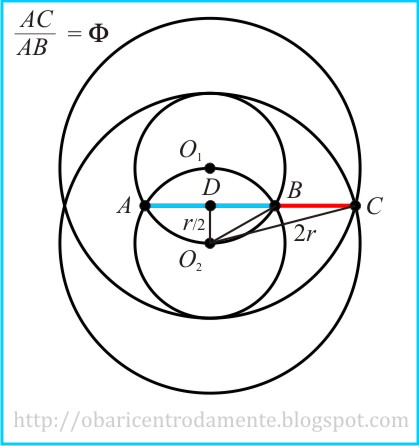
O problema se resume em determinar as medidas dos segmentos AC e AB. Para isso, considere a figura abaixo:
Vamos determinar primeiramente o comprimento do segmento DB = AD. Considere o triângulo retângulo O2BD. Pelo teorema pitagórico, temos que:
Para determinarmos o comprimento do segmento DC, aplicamos o teorema pitagórico no triângulo O2CD:
O comprimento AC é dado por:
A razão áurea é dada por:
Esta construção foi desenvolvida por Kurt Hofstetter em 2002 e publicada no Forum Geometricorum, volume 2 em 2002.
Veja mais:
Construção Geométrica de PHI em Circunferências (Parte 1)
Construção Geométrica de PHI em Circunferências (Parte 2)
Construção Geométrica de PHI em Circunferências (Parte 3)


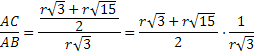

Olá, Kleber!
ResponderExcluirSaímos da "obrigação" de sempre se usar três circunferências para se achar a dimensão áurea. Rsrsrs! Parece complicado, mas, não é, uma vez que os valores dos raios "amarram" a precisão geométrica do desenho. Depois, os Cálculos já são por demais conhecidos, quando trabalhamos com o triângulo retângulo fazendo uso do teorema de Pitágoras.
Com você, não há problema que não fique... atraente de se ver e fácil de se entender, meus parabéns!
Um abraço!!!!!
Olá Valdir!!
ResponderExcluirÉ verdade, não é necessário fazer uso de 3 circunferências para determinar a razão áurea. Mas parece que em muitas construções são nessessárias as condições quanto ao tamanho dos raios, como essa construção por exemplo (r e 2r). Mas de qualquer forma, vale a demonstração por sua beleza e simplicidade de construção.
Algumas outras construções, envolvem apenas 3 segmento de reta (sem nenhuma circunferência) que é muito interessante. Aos poucos vou publicando.
Um abraço.