Construção geométrica de tangentes com régua e compasso - Parte 1

Construções geométricas é um ramo da Matemática muito importante para o desenvolvimento do raciocínio lógico-dedutivo e possui muitas aplicações em desenhos técnicos e mecânicos de máquinas, por exemplo.

Neste artigo, vamos nos concentrar em um problema clássico que é o de traçar tangentes a algumas curvas. Este estudo será dividido em duas partes e nesta primeira parte vamos simplesmente nos abster ao traçado propriamente dito das tangentes à circunferências. Além disso, usaremos os teoremas da Geometria plana para justificar as construções.

1) Traçar uma tangente por um ponto dado sobre a circunferência

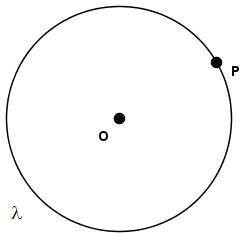
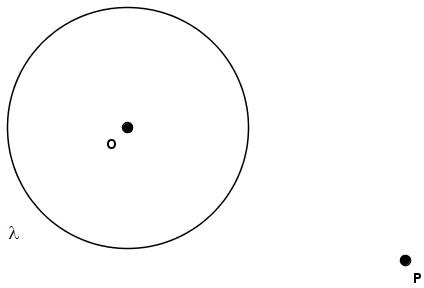
Sejam $\lambda$ uma circunferência de centro $O$ e $P$ pertencente a $\lambda$:

[Figura 1]

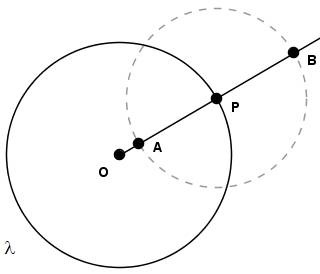
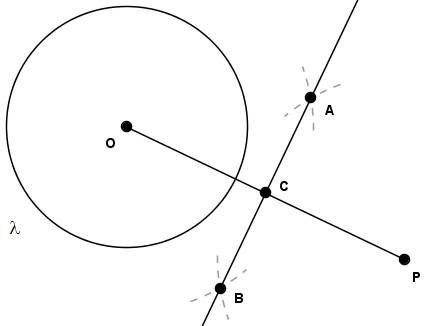
Prolongando o raio $OP$ e com centro em $P$ e abertura do compasso menor que o raio $OP$, determinemos os pontos $A$ e $B$:

[Figura 2]

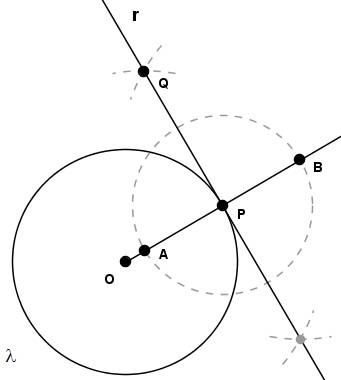
Determinemos, agora, a mediatriz entre os pontos $A$ e $B$ encontrando o ponto $Q$. A reta que passa por $P$ e $Q$ é a reta tangente pedida:

[Figura 3]

Justificativa: A tangente traçada pelo ponto $P$ é uma reta perpendicular ao raio $OP$. Sendo $r$ a mediatriz de $AB$, segue o resultado obtido.

2) De um ponto dado fora de uma circunferência, traçar tangentes a esta circunferência

Sejam $\lambda$ uma circunferência de centro $O$ e raio qualquer e $P$ um ponto não pertencente à $\lambda$:

[Figura 4]

Unindo $O$ e $P$ e tomando a mediatriz de $OP$, que passa pelos pontos $A$ e $B$, determinamos $C$ na intersecção com $OP$:

[Figura 5]

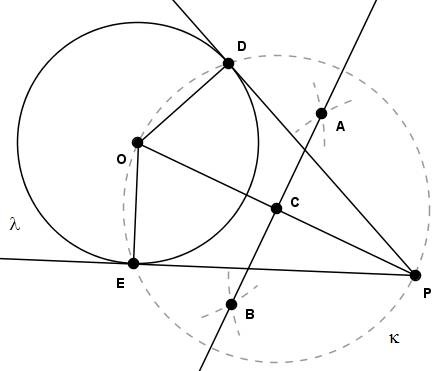
Com centro em $C$ e raio $OC$, traçamos a circunferência $\kappa$ que intercepta $\lambda$ nos pontos $D$ e $E$:

[Figura 6]

As retas que passam por $PD$ e $PE$ são as tangentes pedidas.

Justificativa: As retas tangentes a uma circunferência traçadas de um ponto externo possuem a propriedade de serem perpendiculares ao raio pelos pontos de tangência. Por construção $OP$ é o diâmetro da circunferência $\kappa$ e o triângulo $ODP$ é retângulo em $D$, pois está inscrito na semicircunferência $OAP$.

Outra propriedade é que os segmentos das tangentes a uma circunferência conduzidas por um mesmo ponto são congruentes:

$$
PD \cong PE
$$

3) Traçar as tangentes comuns, exteriores, a duas circunferências

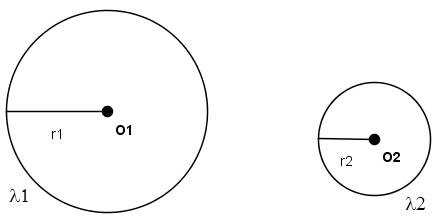
Sejam duas circunferências $\lambda_1$ e $\lambda_2$ de centros $O_1$ e $O_2$, cujos raios $r_1$ e $r_2$ são tais que $r_1+r_2 < d(O_1,O_2)$, ou seja, as circunferências são disjuntas. Suponha também que $r_1<r_2$:

[Figura 7]

Ligando os centros $O_1$ e $O_2$, determinamos a mediatriz que intercepta $O_1O_2$ em $C$.

[Figura 8]

Descrevemos a circunferência $\lambda_3$ de centro $O_1$ e raio $r_3=r_1-r_2$:

[Figura 9]

Observação: Para determinarmos o raio $r_3$, com abertura do compasso igual ao raio de $\lambda_1$, descrevemos uma circunferência de raio $PQ$ com centro em $P$. Em seguida, com abertura do compasso igual ao raio de $\lambda_2$, descrevemos outra circunferência de raio $QR$ centrada em $Q$. A distância $PR$ é o raio da circunferência $\lambda_3$:

[Figura 10]

Com centro em $C$ e raio $O_1C$ descrevemos uma circunferência que intercepta $\lambda_3$ nos pontos $A$ e $B$:

[Figura 11]

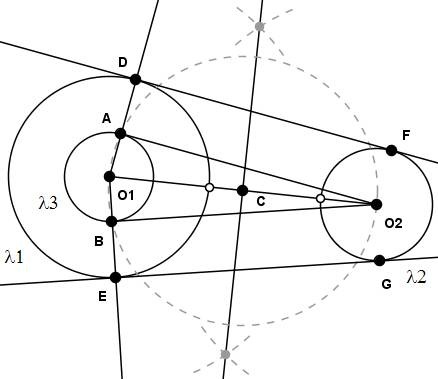
Unimos os pontos $O_2$ e $A$ e os pontos $O_2$ e $B$. Observe que $O_2A$ e $O_2B$ são tangentes externas a $\lambda_3$ traçadas de $O_2$. Prolongamos $O_1A$ até o ponto $D$ pertencente a $\lambda_1$ e também $O_2B$ até o ponto $E$ pertencente a $\lambda_1$. Traçamos em seguida por $D$ um segmento paralelo a $AO_2$ que intercepta $\lambda_2$ no ponto $F$. Analogamente $EG$ é paralelo a $BO_2$.

[Figura 12]

Veja mais:

Construção geométrica de tangentes parte 2

Reta Tangente a uma Curva
Ângulo entre Circunferência e Circunferências Ortogonais