Demonstração da Fórmula do Volume de Pirâmide

Após procurar por um bom tempo uma demonstração convincente da fórmula do volume de uma pirâmide, resolvi botar os neurônios para trabalhar. Demorou um pouco mas consegui descobrir de onde vem aquele 1/3 da área da base pela altura. Para entender a demonstração é necessário conhecer um pouco de cálculo integral.

Parte 1: Demonstração Fórmula Volume Pirâmide de Base Circular

Vamos considerar primeiramente um caso particular de pirâmide: o cone.

Considere a área sombreada sob a curva f (x) = ax:

Podemos notar que a figura formada é um triângulo retângulo com um dos vértices na origem. Se rotacionarmos este triângulo 360º em torno do eixo x, observamos que a figurar formada é um cone com vértice na origem:

Para encontrarmos o volume deste cone, vamos supor fatias paralelas ao eixo y com larguras infinitesimais dx e raio y:

O Volume de um Cilindro é dado por:

Como o raio do cilindro de altura infinitesimal é igual a y e sua altura é igual a dx, podemos reescrever a fórmula de seu volume como:

Podemos dizer que o cone é formado por infinitos  cilindros de alturas infinitesimais dx, onde o raio y é variável para cada cilindro. A soma destes cilindros será dada pela integral definida:

Que equivale a dizer:

onde f (x) é a curva f (x) = ax, x₀ e x₁ são os limites da área sob a curva (o vértice e o centro da base do cone gerado, respectivamente).

Temos então que o volume do cone é dado por:

mas f (x) = ax, portanto:

Integrando em relação a x, temos:

mas como x₀ = 0 (origem), temos:

Em contrapartida temos que:

Substituindo ( II ) em ( I ), obtemos:

Mas y₁ é o raio da base no cone e x₁ é sua altura. Então podemos reescrever o volume como:

Se a área da base do cone é:

Temos que:

Que é a famosa fórmula para cálculo de volume de uma pirâmide qualquer.

 

Exemplo 1: Dado o cone abaixo, calcular seu volume.

Primeiramente, vamos remanejar o cone acima para melhor entendimento:

Se utilizarmos a fórmula pronta para cálculo de volume de pirâmide, temos:

Que é o mesmo valor encontrado utilizando o conceito de integral definida.

 

Parte 2: Demonstração Fórmula Volume Pirâmide de Base Qualquer

Consideremos a pirâmide de base quadrada abaixo:

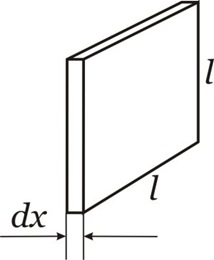
Para encontrarmos o volume desta pirâmide, vamos supor fatias paralelas ao eixo y com alturas infinitesimais dx:

O volume deste prisma de altura infinitesimal é dado por:

Mas l / 2 é igual a y, então:

Podemos dizer que o volume da pirâmide é constituído por infinitos prismas de alturas infinitesimais dx, onde os lados l são variáveis para cada prisma.

A soma destes prismas de alturas infinitesimais é dado pela integral definida:

Integrando em relação a x, temos:

Mas como x₀, então:

Temos que f (x) = ax:

Substituindo (II) em (I), temos:

Mas y₁ é a metade da aresta lateral da base da pirâmide e x₁é sua altura h:

Como a área de base é l², então:

Que é a famosa fórmula para cálculo de volume de uma pirâmide qualquer.

Vimos que numa pirâmide de base circular e quadrada, encontramos a mesma fórmula para o volume. Se quisermos aplicar o mesmo conceito para uma pirâmide de base pentagonal, hexagonal ou n-gonal, veremos que todas recaem à mesma fórmula para o volume.

---

Veja mais:

Demonstração da Fórmula do Volume de Tronco de Cone Partindo da Fórmula do Volume de Pirâmide
Demonstração da Fórmula do Volume de Cone por Semelhança de Triângulo
Demonstração da Fórmula de Tronco de Pirâmide

---