Esta é uma construção geométrica simples, utilizando apenas duas circunferências e um segmento de reta, que relaciona raízes quadradas do tipo $\displaystyle \sqrt{3R^2}$.
Teorema 1:
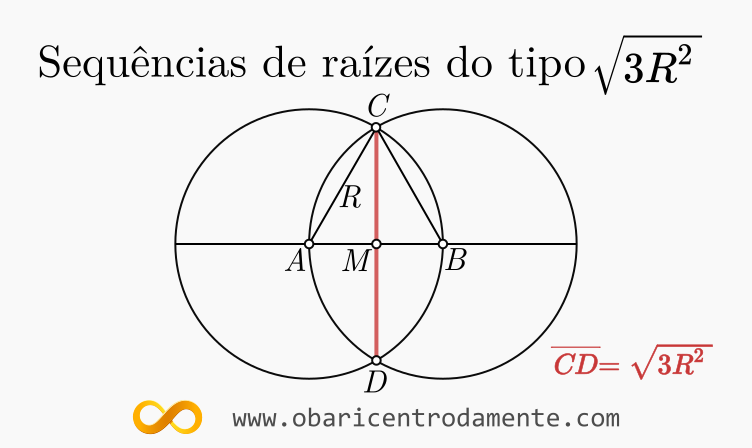
Seja a circunferência $C_1$ de raio $R$ de centro $A$. Seja a circunferência $C_2$ de raio $R$ que passe por $A$ centrada em $B$. Marque as intersecções entre as circunferências como $C$ e $D$. Então o segmento $\displaystyle \overline{CD}=\sqrt{3R^2}$.
Demonstração:
Por construção o triângulo $ABC$ é equilátero, cujos lados medem $R$. Seja $M$ o ponto médio entre os centros das circunferências e seja $h$ o segmento $\overline{CM}$. Pelo teorema pitagórico, temos que:
\begin{equation*}R^2=h^2+\left( \frac{R}{2}\right)^2 \Rightarrow h=\frac{\sqrt{3R^2}}{2}
\end{equation*}
Mas $\overline{CD}=2h$, logo:
\begin{equation*}
\overline{CD}=\sqrt{3R^2}
\end{equation*}
Considerando raios de valores inteiros, podemos construir uma tabela:
Corolário 1:
A área do quadrado construído sobre o segmento $\overline{CD}$ vale $A=3R^2$.
Demonstração:
Sendo $R=\overline{AB}$, $\overline{CD}=\sqrt{3R^2}$, que é um dos lados do quadrado, sua área é dada por:
\begin{equation*}A=\overline{CD}^2=\left(\sqrt{3R^2} \right)^2=3R^2
\end{equation*}
Podemos montar uma tabela:
Vejam que para $R\in \mathbb{N}$, temos uma sequência numérica para a área do quadrado construído. Para valores de $R$ até $100$, temos:
3,
12, 27, 48, 75, 108, 147, 192, 243, 300, 363, 432, 507, 588, 675, 768,
867, 972, 1083, 1200, 1323, 1452, 1587, 1728, 1875, 2028, 2187, 2352,
2523, 2700, 2883, 3072, 3267, 3468, 3675, 3888, 4107, 4332, 4563, 4800,
5043, 5292, 5547, 5808, 6075, 6348, 6627, 6912, 7203, 7500, 7803, 8112,
8427, 8748, 9075, 9408, 9747, 10092, 10443, 10800, 11163, 11532, 11907,
12288, 12675, 13068, 13467, 13872, 14283, 14700, 15123, 15552, 15987,
16428, 16875, 17328, 17787, 18252, 18723, 19200, 19683, 20172, 20667,
21168, 21675, 22188, 22707, 23232, 23763, 24300, 24843, 25392, 25947,
26508, 27075, 27648, 28227, 28812, 29403, 30000
Vejam que a sequência acima é uma P.A. de segunda ordem, pois:
\begin{equation*}a_{N-1}-a_N=b_N \qquad \text{onde} \qquad b_N=b_1+(N-1)r
\end{equation*}
Montemos uma tabela com os $10$ primeiros termos da sequência para uma análise:
A P.A. definida pelos termos $b_N$ tem razão aritmética $r=6$. Por definição, numa P.A., a diferença entre um termo e seu antecessor é uma constante denominada $r$, o que justifica na tabela acima $N>1$.






Chamando a sequência acima de a_n, observamos que a_{n+1} - a_n = b_n, onde b_n é uma PA de 1ª ordem.
ResponderExcluirb_n = ( 9, 15, 21, 27, 33, 39, ...)
Logo, por definição, a sequência a_n é uma PA de 2ª ordem.
Olá Aldeck. Bem observado. Já incluí um complemento.
ExcluirAbraços.
Como se demonstra que (a_n) é uma PA de segunda ordem? É que eu "vi" (ou "observei") que os 100 primeiros termos constituem uma PA de segunda ordem. Esta observação mostra que (a_n) é uma PA de segunda ordem para n variando de 0 a 100. Contudo isto não implica que (a_n) é uma PA de segunda ordem para n variando nos inteiros positivos.
ResponderExcluirDizemos que uma sequência $(a_n)$ é uma P.A. de segunda ordem se as diferenças entre os termos consecutivos é uma P.A. não-estacionária, isto é
Excluir$a_{n+1} - a_n = b_n$ onde $b_n = b_1 + (n-1)r;$
Veja a tabela acima.
Leia o artigo neste link:http://fatosmatematicos.blogspot.com.br/2009/12/pas-de-segunda-ordem.html
A tabela só tem 10 linhas. Como se prova que o padrão observado na tabela persiste ad infinitum?. Se o padrão não persistir, a_n não é uma PA de segunda ordem.
ExcluirPodemos testar os valores obtidos nas fórmulas e verificar que o padrão persiste. Mas enquanto não tiver uma demonstração, talvez por indução, os resultados ficam somente como uma verificação.
Excluir