A notação sigma para somas

A definição formal de integral definida envolve a soma de uma quantidade muito grande de termos, tornando-se necessária uma notação especial.

No simbolismo matemático usamos a letra grega maiúscula Sigma, representada pelo glifo $\displaystyle \sum$, correspondente à letra latina $S$, e é chamada de Notação Sigma. Não por acaso é a primeira letra da palavra soma, que ajuda a lembrar o propósito da notação sigma, designando a ideia de somatório ou adição.

Quando usamos o símbolo $\displaystyle \sum$, queremos representar a soma de todos os termos que obedecem a uma forma geral. Assim:

$$ \sum _{k=m}^n a_k=a_m+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_n $$

Lê-se: A soma de $a_k$, com $k$ assumindo valores que variam de $m$ a $n$.

A variável $k$ é o índice do somatório e designa uma valor inicial chamado limite inferior igual a $m$, assumindo valores inteiros até alcançar o limite superior igual a $n$.

Não necessariamente o índice é representado pela letra $k$. Podemos usar as letras $i$, $j$, $k$, ou outra qualquer dependendo da necessidade, servindo ao mesmo propósito. Então:

$$ \sum_{k=1}^N a_k = \sum_{i=1}^N a_i = \sum_{j=1}^N a_j $$

Se quisermos somar os números naturais de $2$ a $6$, por exemplo, escrevemos na notação de somatório:

$$ \sum_{k=2}^6 k = 2+3+4+5+6 $$

Vejamos outros exemplos específicos na notação sigma:

Exemplo 1:

$$ \sum_{k=1}^5 k^2 = 1^2 + 2^2 +3^2+4^2+5^2 $$ $$ \sum_{k=1}^5 k^2=1+4+9+16+25 $$ $$ \sum_{k=1}^5 k^2=55 $$

Esta é a soma dos quadrados dos cinco primeiros números naturais.

Exemplo 2:

$$ \sum_{k=1}^4 2^k =2^1+2^2+2^3+2^4 $$ $$ \sum_{k=1}^4 2^k =2+4+8+16 $$ $$ \sum_{k=1}^4 2^k =30 $$

Esta é a soma das quatro primeiras potências de $2$.

Exemplo 3:

$$ \sum_{k=1}^N 2k =2+4+6+\cdots+2N $$

Esta é a soma dos $N$ primeiros números pares.

Exemplo 4:

$$ \sum_{k=1}^N (2k-1)=1+3+5+\cdots+(2N-1) $$

Esta é a soma dos $N$ primeiros números ímpares.

Exemplo 5:

$$ \sum_{k=1}^N (3^k-3^{k-1})=(3^1-3^0)+(3^2-3^1)+\cdots+(3^N-3^{N-1}) $$

Aqui fazemos uma pequena manipulação:

$$ \sum_{k=1}^N (3^k-3^{k-1})=-3^0+(3^1-3^1)+(3^2-3^2)+\cdots +(3^{N-1}-3^{N-1})+3^N $$

$$ \sum_{k=1}^N (3^k-3^{k-1})=3^N-3^0=3^N-1 $$

Exemplo 6:

$$ \sum_{k=1}^N k =1+2+3+\cdots+N $$ $$ \sum_{k=1}^N k = \frac{N(N+1)}{2} $$

Esta é a fórmula para a soma dos $N$ termos de uma P.A. finita.

Exemplo 7:

Podemos ainda fazer o processo inverso: dada uma sequência, vamos encontrar a notação sigma:

$$ 3+9+27+81 = 3^1+3^2+3^3+3^4= \sum_{k=1}^4 3^k $$

Exemplo 8:

$$ 5+9+13+17+21+15 $$

$$ = 5+(5+4)+(5+8)+(5+12)+(5+16)+(5+20) $$

$$ = 5+(5+4)+(5+4\cdot 2)+(5+4\cdot 3)+(5+4\cdot 4)+(5+4\cdot 5) $$

$$ = \sum_{k=0}^5 (5+4k) $$

A Notação Sigma é essencialmente útil para indicar a soma dos termos de uma sequência numérica. Normalmente, quando trabalhamos com sequências, é conveniente começar com um termo de ordem zero: $a_0$. Assim, o segundo termos é $a_1$, o terceiro é $a_2$, e assim por diante. Podemos escrevê-la como $a_0, a_1, a_2, \cdots $. Assim, o k-ésimo termo da sequência é $a_k$ e a soma dos $N$ termos pode ser escrita como:

$$ \sum_{k=0}^N a_k=a_0+a_1+a_2+\cdots + a_N $$

Se quisermos somar apenas o terceiro, o quarto e o quinto termos, escrevemos:

$$ \sum_{k=2}^4 a_k=a_2+a_3+a_4 $$

Propriedades Básicas dos Somatórios

Algumas propriedades básicas dos somatórios podem ser estabelecidas. Consideremos que $a_0, a_1, a_2, \cdots, a_N$ e $b_0, b_1, b_2, \cdots , b_N$, representam sequências de números e seja $A, B,C$ números constantes.

P1 - Propriedade da Constante

$$ \sum_{k=1}^N C= NC $$

P2 - Propriedade da Homogenidade

$$ \sum_{k=1}^N Ca_k = C\sum_{k=1}^N a_k $$

P3 - Propriedade Aditiva

$$ \sum_{k=1}^N \left(a_k+b_k\right)=\sum_{k=1}^N a_k + \sum_{k=1}^N b_k $$

P4 - Propriedade Linear

$$ \sum_{k=1}^N \left(Aa_k + Bb_k\right) = A\sum_{k=1}^N a_k + B\sum_{k=1}^N b_k $$

P5 - Desigualdade Triangular Generalizada

$$ \left| \sum_{k=1}^N a_k \right| \leq \sum_{k=1}^N \left| a_k \right| $$

P6 - Propriedade Telescópica

$$ \sum_{k=1}^N \left(b_k - b_{k-1}\right) = b_N - b_0 $$

P7 - Soma de uma Sequência Aritmética

$$ \sum_{k=0}^N \left(A+Ck\right) = \left(N+1\right)\left(A+\frac{NC}{2}\right) $$

P8 - Soma de uma Sequência Geométrica

$$ \sum_{k=0}^N AC^k = A\left(\frac{1-C^{N+1}}{1-C}\right), \qquad C\neq 1 $$

P9 - Soma dos Inteiros Sucessivos

$$ \sum_{k=1}^N k = \frac{N(N+1)}{2} $$

P10 - Soma dos Quadrados Sucessivos

$$ \sum_{k=1}^N k^2 = \frac{N(N+1)(2N+1)}{6} $$

P11 - Soma dos Cubos Sucessivos

$$ \sum_{k=1}^N k^3 = \frac{N^2(N+1)^2}{4} $$

Exemplos usando as propriedades básicas dos somatórios:

Exemplo 9:

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right) $$

Usamos a propriedade P4:

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right) = \sum_{k=1}^{20} 2k^2+\sum_{k=1}^{20}(-3k)+\sum_{k=1}^{20} 1 $$

Agora, usamos as propriedades P1 e P2:

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right) = 2\sum_{k=1}^{20}k^2 - 3\sum_{k=1}^{20}k + 20 $$

Agora usamos a propriedade P10 no primeiro somatório e a P9 no segundo:

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right) = \frac{2(20)(21)(41)}{6}-\frac{3(20)(21)}{2}+20 $$

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right) = 5740-630+20 $$

$$ \sum_{k=1}^{20} \left(2k^2-3k+1\right)=5130 $$

Exemplo 10:

$$ \sum_{k=1}^N k^2(5k+1) $$

$$ \sum_{k=1}^N k^2(5k+1)=\sum_{k=1}^N5k^3+\sum_{k=1}^N k^2 $$

$$ \sum_{k=1}^N k^2(5k+1)=5\left(\frac{N^2(N+1)^2}{4}\right) + \frac{N(N+1)(2N+1)}{6} $$

$$ \sum_{k=1}^N k^2(5k+1)= \frac{5N^2(N+1)^2}{4} + \frac{N(N+1)(2N+1)}{6} $$

$$ \sum_{k=1}^N k^2(5k+1)=N(N+1)\left(\frac{5N(N+1)}{4}+\frac{2N+1}{6}\right) $$

$$ \sum_{k=1}^N k^2(5k+1)=N(N+1)\left(\frac{15N(N+1)+2(2N+1)}{12}\right) $$

$$ \sum_{k=1}^N k^2(5k+1)=\frac{N(N+1)(15N^2+15N)+2N+2}{12} $$

$$ \sum_{k=1}^N k^2(5k+1)=\frac{(N^2+N)(15N^2+15N)+2N+2}{12} $$

$$ \sum_{k=1}^N k^2(5k+1)=\frac{15N^4+15N^3+15N^3+15N^2+2N+2}{12} $$

$$ \sum_{k=1}^N k^2(5k+1)=\frac{15N^4+30N^3+15N^2+2N+2}{12} $$

$$ \sum_{k=1}^N k^2(5k+1)=\frac{15N^2(N^2+2N+1)+2(N+1)}{12} $$

Exemplo 11:

$$ \sum_{k=0}^N \frac{1}{2^k} $$

Usando a propriedade P8:

$$ \sum_{k=0}^N \frac{1}{2^k}=\sum_{k=0}^N \left(\frac{1}{2}\right)^k $$

$$ \sum_{k=0}^N \frac{1}{2^k}= \frac{\displaystyle 1-\left(\frac{1}{2}\right)^{N+1}}{\displaystyle 1-\frac{1}{2}} $$

$$ \sum_{k=0}^N \frac{1}{2^k}= 2-\frac{1}{2^N} $$

Exemplo 12:

Encontre a soma dos $100$ primeiros inteiros ímpares.

Pela propriedade P7, fazemos $A=1$, $C=2$, $N=99$:

$$ \sum_{k=0}^{99} (1+2k)=1+3+5+\cdots +199 $$

$$ \sum_{k=0}^{99} (1+2k)=100\left(1+\frac{99(2)}{2}\right) $$

$$ \sum_{k=0}^{99} (1+2k)=10.000 $$

A Área sob uma Parábola

Este é um bom exemplo para aplicarmos a notação sigma. Calculemos a área $A$ sob a parábola $y=x^2$ entre $x=0$ e $x=1$.

Usando o conceito de integral definida, obtemos:

$$ A=\int_0^1 x^2dx=\left[\frac{x^3}{3}\right]_0^1=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \text{ u.a.} $$

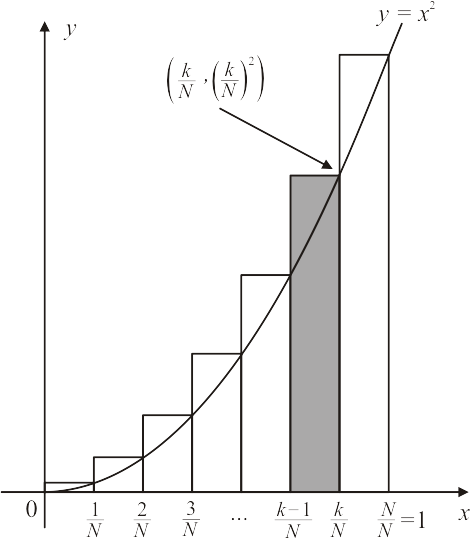
Agora, usemos a notação sigma. Considere a figura abaixo:

O intervalo $[0,1]$ foi subdividido em subintervalos iguais:

$$ \left[0,\frac{1}{N}\right] ,\left[\frac{1}{N},\frac{2}{N}\right] , \left[\frac{2}{N},\frac{3}{N}\right],\cdots ,\left[\frac{N-1}{N},\frac{N}{N}\right] $$

Vejam que o k-ésimo intervalo é:

$$ \left[\frac{k-1}{N},\frac{k}{N}\right] $$

Em cada subintervalo, podemos formar um retângulo circunscrito à curva, cuja altura do k-ésimo retângulo é $\displaystyle \left(\frac{k}{N}\right)^2$ e sua área é $\displaystyle \frac{1}{N}\cdot \left(\frac{k}{N}\right)^2$.

Podemos obter uma estimativa para a área $A$ somando as áreas dos $N$ retângulos circunscritos:

$$ A\approx \sum_{k=1}^N \frac{1}{N}\left(\frac{k}{N}\right)^2 $$

E pela fórmula para a soma dos quadrados sucessivos:

$$ A\approx \sum_{k=1}^N \frac{1}{N}\left(\frac{k}{N}\right)^2 \\ \ \\ A\approx \sum_{k=1}^N \left(\frac{1}{N^3}\right)k^2\\ \ \\ A\approx \left(\frac{1}{N}\right)^3 \sum_{k=1}^N k^2\\ \ \\ A\approx \frac{1}{N^3} \left( \frac{N(N+1)(2N+1)}{6}\right)\\ \ \\ A\approx \frac{(N+1)(2N+1)}{6N^2} $$

Aplicando a distributiva no numerador, segue que:

$$ A\approx \frac{1}{3}+\frac{1}{2N}+\frac{1}{6N^2} $$

Como os retângulos são circunscritos à curva e somente aproximam a área, então:

$$ A \leq \frac{1}{3} + \frac{1}{2N} + \frac{1}{6N^2} $$

Utilizemos agora, retângulos inscritos à mesma curva no mesmo intervalo, com os mesmos $N$ subintervalos:

Notamos que a altura do k-ésimo retângulo inscrito é $\displaystyle \left(\frac{k-1}{N}\right)^2$ e sua área é $\displaystyle \frac{1}{N}\left(\frac{k-1}{N}\right)^2$.

Novamente podemos obter uma estimativa para a área $A$, somando as áreas dos $N$ retângulos inscritos:

$$ A\approx \sum_{k=1}^N \frac{1}{N}\left(\frac{k-1}{N}\right)^2 $$

$$ A\approx \frac{1}{N^3}\sum_{k=1}^N (k^2-2k+2) $$

$$ A\approx \frac{1}{N^3}\left(\sum_{k=1}^N k^2-2\sum_{k=1}^Nk+\sum_{k=1}^N\right) $$

$$ A\approx \frac{1}{N^3}\left(\frac{N(N+1)(2N+1)}{6}-\frac{2N(N+1)}{2}+N\right) $$

$$ A\approx \frac{2N^2-3N+1}{6N^2} $$

Então, a área vale aproximadamente:

$$ A\approx \frac{1}{3}-\frac{1}{2N}+\frac{1}{6N^2} $$

Como os retângulos são inscritos à curva e somente aproxima a área, então:

$$ A\geq \frac{1}{3}-\frac{1}{2N}+\frac{1}{6N^2} $$

Deste modo, a área $A$ sob a curva, tem que estar entre as duas estimativas encontradas, de modo que:

$$ \frac{1}{3}-\frac{1}{2N}+\frac{1}{6N^2}\leq A \leq \frac{1}{3}+\frac{1}{2N}+\frac{1}{6N^2} $$

$$ \sum_{k=1}^N\frac{1}{N}\left(\frac{k-1}{N}\right)^2 \leq A \leq \sum_{k=1}^N \frac{1}{N}\left(\frac{k}{N}\right)^2 $$

À medida que $N$ aumenta, ambas as estimativas se aproximam de um valor, tendo $1/3$ como limite. Como a área $A$ está entre as duas estimativas, podemos nos aproximar o quanto desejarmos do valor limite $1/3$, tomando cada vez mais subintervalos. Quando o número de subintervalos tende ao infinito, a área $A$ sob a curva $f(x)=x^2$, no intervalo $[0,1]$ tende a ser igual a $1/3$.

Exercícios: Desenvolva os somatórios

a) $\displaystyle \sum_{k=1}^6 (2k+1)$

b) $\displaystyle \sum_{k=3}^7 \frac{k}{k-2}$

c) $\displaystyle \sum_{k=-1}^3 3^k$

d) $\displaystyle \sum_{k=1}^{50}(2k+3)$

e) $\displaystyle \sum_{k=1}^N k(k+1)$

f) $\displaystyle \sum_{k=6}^{100}k^2$

g) $\displaystyle \sum_{k=1}^{\infty}\frac{1}{k(k+1)}$

Referências:

• Cálculo V1 - Munem-Foulis
• Cálculo com Geometria Analítica V1 - Simmons

Veja mais:

• A Soma de Gauss
• O Cálculo Integral: O Cálculo das Áreas
• Como Kepler quase descobriu o Cálculo