Trabalhando com Frações

Objetivos:

Desenvolver através de brincadeiras, o aprendizado, raciocínio e manipulação de frações.

Material utilizado:

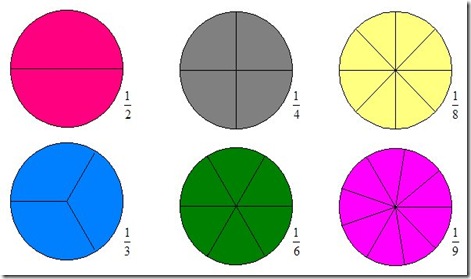
- 6 círculos de madeira, cortados de modo a formarem fatias equivalentes às frações:

1/2, 1/3, 1/4, 1/6, 1/8 e 1/9

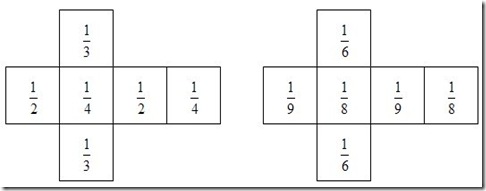
- 2 dados, onde o primeiro dado terá faces numeradas com

1/2, 1/3 e 1/4

e o segundo dado com faces numeradas com:

1/6 , 1/8 e 1/9

Os círculos:

Os dados:

O jogo:

A idéia é completar 1 inteiro (círculo completo) utilizando várias fatias de valores diferentes. Para isso utilizaremos 2 dados e 6 círculos fatiados de maneiras diferentes.

Regras do jogo:

Joga-se os dados, obtendo uma combinação de frações entre eles;

Soma-se as duas parcelas;

Para visualizar a quantidade obtida, tomamos os valores de cada dado e associamos às peças correspondentes de cada fatia dos círculos, unindo-as e obtendo uma fatia equivalente;

Calculamos o quanto falta para obtermos 1 inteiro (círculo completo);

Utilizando as fatias que sobram, devemos completar a círculo;

Para completarmos 1 inteiro, devemos utilizar no mínimo 2 fatias.

Possibilidades de combinações:

Dado 1:

1/2 , 1/3 e 1/4

Dado 2:

1/6, 1/8 e 1/9

Total de 9 combinações diferentes.

Desenvolvimento teórico das combinações:

- Combinação 1:

1/2 + 1/6 = 2/3, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 1/3. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser 1/3 ou 1/6+1/6.

- Combinação 2:

1/2 + 1/8 = 5/8, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 3/8. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 1/8 + 1/8 +1/8 ou 1/8 + 1/4.

Combinação 3:

1/2 + 1/9 = 11/18, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 7/18. Poderíamos adicionar 7 fatias de 1/18, mas como o jogo não possui fatias com esse valor, temos que achar combinações equivalente a 7/18.

Se somarmos uma fatia de 1/6 à 11/18, obteremos 7/9. Para completarmos 1 inteiro, devemos adicionar 2/9. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 1/9 + 1/9.

- Combinação 4:

1/3 + 1/6 = 1/2, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 1/2. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por algumas combinações: 1/2, 1/4 + 1/4, 1/4 + 1/8 + 1/8 ou 1/8 + 1/8 + 1/8 + 1/8.

- Combinação 5:

1/3 + 1/8 = 11/24, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 13/24. Poderíamos adicionar 13 fatias de 1/24, mas como o jogo não possui fatias com esse valor, temos que achar combinações equivalente a 13/24.

Se somarmos 1/6 à 11/24, obteremos 5/8. Para completarmos 1 inteiro, devemos adicionar 3/8. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 3 fatias de 1/8 ou 1/8 + 1/4.

- Combinação 6:

1/3 + 1/9 = 4/9, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 5/9. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 5 fatias de 1/9 ou 1/9 + 1/9 + 1/3.

- Combinação 7:

1/4 + 1/6 = 5/12, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 7/12. Poderíamos adicionar 7 fatias de 1/12, mas como o jogo não possui fatias com esse valor, temos que achar combinações equivalente a 7/12.

Se somarmos 1/3 à 5/12, obteremos 3/4. Para completarmos 1 inteiro, devemos adicionar 1/4. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 1/4 ou 1/8 + 1/8.

Se somarmos 1/4 à 5/12, obteremos 2/3. Para completarmos 1 inteiro, devemos adicionar 1/3. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 1/3 ou 1/6 + 1/6.

- Combinação 8:

1/4 + 1/8 = 3/8, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 5/8. Pegamos a fatia correspondente e encaixamos no círculo, que pode ser composta por 5 fatias de 1/8 ou 1/8 + 1/2 ou 1/4 + 1/4 + 1/8 ou 1/4 + 1/8 + 1/8 + 1/8.

- Combinação 9:

1/4 + 1/9 = 13/36, para completarmos o círculo e formarmos 1 inteiro, devemos adicionar 23/36. Poderíamos adicionar 23 fatias de 1/36, mas como o jogo não possui fatias com esse valor, temos que achar combinações equivalente a 23/36.

Se somarmos qualquer uma das fatias disponíveis no jogo, ainda assim não conseguiríamos completar 1 inteiro sem mesmo fazer outras combinações.

Utilizando as fatias disponíveis e encaixando-as, logo chegaríamos à conclusão que se somarmos 1/6, 1/4, 1/9, 1/9 à 13/36, obteremos 1 inteiro.

Neste caso, pela álgebra, conseguimos um desenvolvimento interessante, podemos dizer que:

23/36 = A/B + C/D + E/F

Sabemos que, através do princípio de equivalência de frações, a soma dos termos dos denominadores, B, D e F, tem que ser igual a 36.

Tomando todas as frações disponíveis do jogo (1/2, 1/3, 1/4, 1/6, 1/8, 1/9), a única combinação possível para que tenhamos, através da soma, o denominador igual a 36 é: 4, 6 e 9.

Então temos:

23/36 = A/4 + C/6 + E/9

logo temos que:

23/36 = (9A + 6C + 4E) / 36

Usando do princípio de equivalência de frações, temos:

23 = 9A + 6C + 4E

Agora temos que descobrir os valores de A, C e E, dentro dos padrões de peças do jogo, para satisfazer a equação.

Tomando A=1, C=1 e E=2, temos:

23/36 = (9.1 + 6.1 + 4.2) / 36

23/36 = 23/36

Então, as frações procuradas são 1/4, 1/6 e 2/9.

Utilizando as peças, temos que, para completar 1 inteiro, precisaremos de fatias equivalentes a 1/4, 1/6, 1/9 e 1/9.

Exposição:

Reunir grupos em salas de aula de 4 pessoas para poderem raciocinar de maneira mais rápida e intuitiva e acompanhar o desenvolvimento de cada um.

Horas gastas no Projeto:

Elaboração e desenvolvimento da teoria: 3h.

Digitação e desenho das figuras: 5h.

Total gasto: 8h.