Neste artigo, veremos alguns exemplos de otimização fazendo uso de derivadas.
Para encontrarmos os valores de máximo ou mínimo, primeiramente devemos encontrar a função que nos leva à solução do problema, calcular sua derivada e obter uma função que dependa somente de uma variável. Em seguida, igualamos a zero, obtendo uma equação. E por fim, calculamos seu valor e obtendo o valor de máximo ou de mínimo.
Exemplo 1:
Dado um cone de geratriz igual a $5\ cm$, determinar suas dimensões de modo que se tenha o maior volume possível.
Primeiramente, vamos esboçar um cone genérico, destacando o triângulo retângulo:
Lembrando que o volume do cone é dado por:
$$
V = \frac{1}{3} \cdot A_b \cdot h = \frac{1}{3}\ h\ \pi\ r^2 \tag{1.1}
$$
Dos dados fornecidos no enunciado do problema, temos que:
$$
5^2 = r^2 + h^2\\
\ \\
25 = r^2 + h^2
$$
Obtemos:
$$
r^2 = 25-h^2 \tag{1.2}
$$
Substituindo o valor de $r$ da relação $(1.2)$ na fórmula do volume do cone:
$$
V = \frac{1}{3}\ h\ \pi (25-h^2)\\
\ \\
V = \frac{25\ \pi\ h}{3} - \frac{\pi\ h^3}{3}
$$
Vamos agora calcular a derivada da função $V(h)$:
$$
V(h) = \frac{25\ \pi\ h}{3} - \frac{\pi\ h^3}{3}\\
\ \\
V^\prime = \frac{25\ \pi}{3} - \frac{3\pi\ h^2}{3}\\
\ \\
V^\prime = \frac{25\ \pi}{3} - \pi\ h^2
$$
Igualamos a zero para obtermos uma equação que nos leve ao valor de máximo:
$$
\frac{25\ \pi}{3} - \pi\ h^2 = 0\\
\ \\
\pi\ h^2 = \frac{25\ \pi}{3}\\
\ \\
h^2 = \frac{25}{3}\\
\ \\
h = \frac{5}{\sqrt{3}}\\
\ \\
h = \frac{5\sqrt{3}}{3}\\
\ \\
h \approx 2,88\ cm
$$
Encontramos a altura $h$ do cone. Agora, para encontrar o raio $r$ de sua base, substituímos o valor de $h$ na relação $(1.1)$:
$$
r^2 = 25 - h^2\\
\ \\
r^2 = 25 - \left(\frac{5\sqrt{3}}{3}\right)^2\\
\ \\
r^2 = 25 - \frac{25 \cdot 3}{9}\\
\ \\
r^2 = 25 - \frac{25}{3}\\
\ \\
r^2 = \frac{75-25}{3}\\
\ \\
r^2 = \frac{50}{3}\\
\ \\
r^2 = \frac{5\sqrt{2}}{\sqrt{3}}\\
\ \\
r^2 = \frac{5\sqrt{6}}{3}\ cm
$$
O cone que possui geratriz igual a $5\ cm$ e que possui o maior volume é o que possui as medidas:
Raio igual a : $\displaystyle r = \frac{5\sqrt{6}}{3} \approx 4,08\ cm$
Altura igual a: $\displaystyle h = \frac{5\sqrt{3}}{3} \approx 2,88\ cm$.
Exemplo 2:
Deseja-se confeccionar uma trave para um campo de futebol com uma viga de $18\ m$ de comprimento. Encontre as dimensões para que a área do gol seja máxima.
Iniciamos esboçando um desenho de uma trave genérica:
Pelos dados fornecidos no enunciado do problema, temos que:
$$
2x + y = 18
$$
Isolando $y$, obtemos:
$$
y = 18 - 2x \tag{2.1}
$$
A área do gol é dada pela fórmula da área de um retângulo:
$$
A = x \cdot y \tag{2.2}
$$
Substituindo a relação $(2.1)$ em $(2.2)$, obtemos:
$$
A = x(18 - 2x)\\
\ \\
A = 18x - 2x^2
$$
Agora, calculamos a derivada da função $A(x)$:
$$
A(x) = 18x - 2x^2\\
\ \\
A^\prime = 18 - 4x
$$
Igualamos a zero para obtermos uma equação linear que nos leve ao cálculo de máximo:
$$
18-4x=0\\
\ \\
4x=18\\
\ \\
x = \frac{9}{2}\\
\ \\
x = 4,5
$$
Encontramos a altura $x$ da trave. Para encontrarmos seu comprimento, substituímos o valor de $x$ na relação $(2.1)$:
$$
y = 18 - 2x\\
\ \\
y = 18 - 2\cdot \frac{9}{2}\\
\ \\
y = 18 - 9\\
\ \\
y = 9
$$
Portanto, a trave deverá ter altura de $4,5\ m$ e comprimento de $9\ m$ para que a área do gol seja a maior possível.
As dimensões oficiais de uma trave de futebol são dois postes de $2,44\ m$ e um travessão de $7,32\ m$.
Exemplo 3:
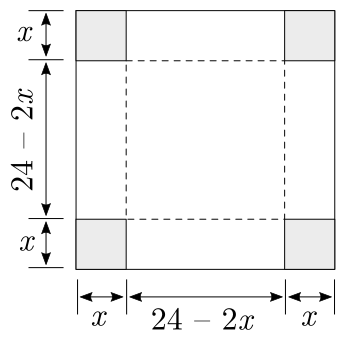
Um fabricante de caixas de papelão pretende construir caixas sem tampas a partir de folhas quadradas de cartão com área igual a $576\ cm^2$, cortando quadrados iguais nos quatro cantos e dobrando os lados para cima. Determinar o lado do quadrado que deve ser cortado para se obter uma caixa com o maior volume possível.
Interpretando o enunciado, podemos esboçar:
Como a área total é de $576\ cm^2$, o lado da folha vale:
$$
A = \ell^2\\
\ \\
576 = \ell^2\\
\ \\
\ell = 24\ cm
$$
O volume da caixa é dado pelo produto da área da base e sua altura:
$$
V = A_b \cdot h\\
\ \\
V = \ell^2 \cdot x\\
\ \\
V = (24-2x)^2 \cdot x\\
\ \\
V = (576-96x + 4x^2)\cdot x\\
\ \\
V = 4x^3 - 96x^2 + 576x
$$
Calculamos a derivada a função $V(x)$:
$$
V(x) = 4x^3 - 96x^2 + 576x\\
\ \\
V^\prime = 12x^2 -192x + 576
$$
Igualamos a zero, obtendo a equação quadrática:
$$
12x^2-192x+576=0
$$
Dividimos a equação por $12$ para facilitar os cálculos:
$$x^2 - 16x + 48 = 0
$$
Aplicamos a fórmula de Bháskara:
$$
x = \frac{-b\pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{16 \pm \sqrt{64}}{2}\\
\ \\
x = \frac{16 \pm 8}{2}\\
\ \\
x_1 = 12\\
\ \\
x_2 = 4
$$
Encontramos dois valores para $x$, mas vejam que somente $x_2=4$ satisfaz o problema, já que temos o lado da folha igual a $\ell = 24-2x$ e se substituirmos $x_1=12$ na relação, obteremos um lado nulo. O que não faz sentido. Então, a caixa deverá ter as dimensões:
Para o lado:
$$
\ell = 24-2x\\
\ \\
\ell = 24 - 8\\
\ \\
\ell = 16\ cm^2
$$
E para a altura:
$$
h=x\\
\ \\
h = 4\ cm
$$
Exemplo 4:
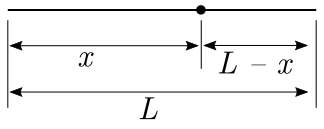
Dividindo um arame de comprimento $L$ em duas partes, faz-se com uma das partes uma circunferência e com a outra um quadrado. Determinar o ponto em que se deve cortar o arame para que a soma das áreas geradas pelo quadrado e circunferência seja mínima.
Vamos fazer uma figura representativa:
Vamos adotar que a parte do arame de comprimento $x$ será a que faremos a circunferência $C$ e que a parte de comprimento $L-x$ será o perímetro $P$ do quadrado.
Temos que o comprimento da circunferência é dado por:
$$
C = 2\ \pi\ r\\
\ \\
x = 2\ \pi\ r
$$
Assim:
$$
r = \frac{x}{2\ \pi} \tag{4.1}
$$
A área do círculo é dada por:
$$
A = \pi\ r^2 \tag{4.2}
$$
Substituindo $(4.2)$ na $(4.1)$, obtemos:
$$
A = \pi \left(\frac{x}{2\ \pi}\right)^2
$$
Assim:
$$
A = \frac{x^2}{4} \tag{4.3}
$$
O perímetro do quadrado é dado por:
$$
P = 4 \cdot \ell\\
\ \\
L-x = 4\ \ell
$$
E seu lado vale:
$$
\ell = \frac{L-x}{4} \tag{4.4}
$$
A área do quadrado é dada por:
$$
A = \ell^2 \tag{4.5}
$$
Substituindo $(4.4)$ em $(4.5)$, obtemos:
$$
A = \left( \frac{L-x}{4}\right)^2
$$
Assim:
$$
A = \frac{L^2-2Lx+x^2}{16} \tag{4.6}
$$
Queremos que a soma das áreas do círculo e do quadrado sejam mínima, então somamos as duas áreas, dadas em $(4.3)$ e $(4.6)$:
$$
A_T = \frac{x^2}{4\ \pi} + \frac{L^2-2Lx+x^2}{16}\\
\ \\
A_T = \frac{4x^2+\pi\ L^2 - 2\ \pi\ L\ x + \pi\ x^2}{16\ \pi}\\
\ \\
A_T = \frac{x^2(4+\pi) +\pi\ L^2 - 2\ \pi\ L\ x}{16\ \pi}
$$
Para obter:
$$
A_T = \frac{1}{16\ \pi} \Big[ x^2(4+\pi)+\pi\ L^2 - 2\ \pi\ L\ x \Big] \tag{4.7}
$$
Calculamos agora a derivada da função $A_T(x)$. Vejam que a função está em função de $x$ e $\pi\ L^2$ é uma constante:
$$
A_T(x) = \frac{1}{16\ \pi} \Big[ x^2(4+\pi)+\pi\ L^2 - 2\ \pi\ L\ x \Big] \\
\ \\
A_T^\prime = \frac{1}{16\ \pi} \Big[ x(8+2\ \pi) + 0 - 2\ \pi\ L \Big]\\
\ \\
A_T^\prime = \frac{x(8+2\ \pi)}{16\ \pi} - \frac{2\ \pi\ L}{16\ \pi}\\
\ \\
A_T^\prime = \frac{x(8+2\ \pi)}{16\ \pi} - \frac{L}{8}
$$
Igualamos a zero e obtemos a equação:
$$
\frac{x(8+2\ \pi)}{16\ \pi} - \frac{L}{8} = 0\\
\ \\
\frac{x(8+2\ \pi)}{16\ \pi} = \frac{L}{8}\\
\ \\
x(8 +2\ \pi) = 2\ \pi\ L\\
\ \\
x = \frac{2\ \pi\ L}{8 + 2\ \pi}\\
\ \\
x = \frac{\pi\ L}{4 + \pi}
$$
Portanto, o arame deverá ser cortado no ponto:
$$
x = \frac{\pi\ L}{4 + \pi}
$$
Exemplo 5:
Considere uma família de retângulos onde seus perímetros medem $64\ cm$. Encontrar as medidas de um retângulo em que sua área seja máxima.
Seja o retângulo:
O perímetro de um retângulo é dado por:
$$
P = 2x+2y
$$
Assim:
$$
64 = 2x + 2y
$$
Simplificando:
$$
32 = x + y \tag{5.1}
$$
Da relação acima, obtemos:
$$
x = 32 - y \tag{5.2}
$$
A área de um retângulo é dado por:
$$
A = x \cdot y \tag{5.3}
$$
Substituindo a relação $(5.2)$ em $(5.3)$, obtemos:
$$
A = (32 - y)\cdot y\\
\ \\
A = 32y - y^2
$$
Calculando a derivada da função $A(y)$:
$$
A(y) = 32y - y^2\\
\ \\
A^\prime = 32 - 2y
$$
Igualamos a zero, obtendo a equação:
$$
32 - 2y = 0\\
\ \\
32 = 2y\\
\ \\
y = 16
$$
Agora que encontramos o valor de um dos lados do retângulo, substituímos este valor na relação $(5.2)$:
$$
x = 32- y\\
\ \\
x = 32 - 16\\
\ \\
x = 16
$$
Com este resultado, concluímos que, para que a área seja máxima, o retângulo que possui a maior área é um quadrado cujos lados medem $16\ cm$.
Exemplo 6:
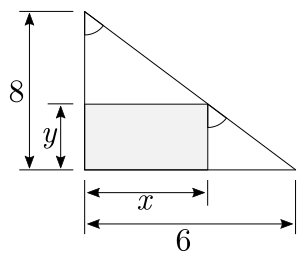
Dada a figura abaixo, encontrar as dimensões do retângulo destacado para que sua área seja máxima.
Temos que encontrar uma equação em termos de $x$ e $y$. Por semelhança de triângulos, temos:
Assim:
$$
\frac{8}{8-y} = \frac{6}{x}\\
\ \\
8x = 48 - 6y
$$
Isolando $x$:
$$
x = 6 - \frac{3}{4}\ y \tag{6.1}
$$
A área do retângulo é dada por:
$$
A = x \cdot y \tag{6.2}
$$
Substituindo o valor de $x$ na $(6.2)$:
$$
A = \left( 6 - \frac{3}{4}\ y\right)\ y\\
\ \\
A = 6y - \frac{3}{4}\ y^2
$$
Calculamos a derivada:
$$
A = 6y - \frac{3}{4}\ y^2\\
\ \\
A^\prime = 6 - \frac{3}{2}\ y
$$
Agora, igualamos a zero:
$$
6 - \frac{3}{2}\ y = 0\\
\ \\
\frac{3}{2}\ y = 6\\
\ \\
3y = 12\\
\ \\
y = 4
$$
Substituindo o valor de $y$ na $(6.1)$:
$$
x = 6 - \frac{3}{4}\cdot 4\\
\ \\
x = 6 - 3\\
\ \\
x = 3
$$
Portanto, para que o retângulo tenha área máxima, seus lados devem medir $3$ e $4$ e sua área será igual a $12$ unidades de área.
Exemplo 7:
Observando a figura abaixo, encontre o valor de $x$ para que a área sombreada seja máxima.
A área sombreada é dada pela diferença das áreas:
$$
A_S = A_Q - (A_1+A_2) \tag{7.1}
$$
Vamos encontrar a área $A_1$:
$$
A_1 = \frac{x \cdot 2x}{2} = x^2 \tag{7.2}
$$
Agora, vamos encontrar a área $A_2$:
$$
A_2 = \frac{4\ (10-x)}{2} = 20-2x \tag{7.3}
$$
Substituindo as relações $(7.2)$ e $(7.3)$ em $(7.1)$, encontramos a função quadrática:
$$
A_S = 100 - (x^2 + 20 - 2x)\\
\ \\
A_S = -x^2 + 2x + 80
$$
Calculamos sua derivada:
$$
A_S^\prime = -2x + 2
$$
Igualamos a zero:
$$
-2x+2=0\\
\ \\
2x=2\\
\ \\
x=1
$$
Agora, já podemos encontrar os valores dos lados dos dois triângulos $1$ e $2$, mas ainda falta encontrar o valor da hipotenusa:
Observando o triângulo $1$, temos que:
$$
H_1^2 = 2^2 + 1^2\\
\ \\
H_1^2 = 4+1\\
\ \\
H_1^2 = 5\\
\ \\
H_1 = \sqrt{5}
$$
Do triângulo $2$, temos que:
$$
H_2^2 = 4^2 + 9^2\\
\ \\
H_2^2 = 16+81\\
\ \\
H_2^2 = 97\\
\ \\
H = \sqrt{97}
$$
Logo, os triângulos possuem as medidas:
Exemplo 8:
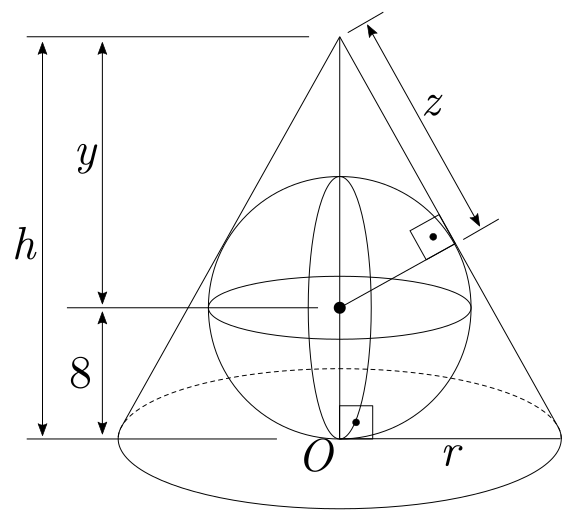
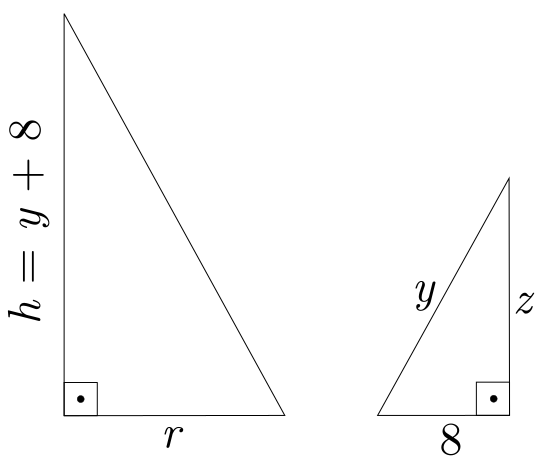
Determinar as medidas do raio e da altura de um cone que contém uma esfera de raio $r=8$ unidades e com volume mínimo.
Analisando a figura acima, podemos destacar dois triângulos retângulos e verificar suas semelhanças:
Do triângulo da direita, temos:
$$
y^2 = z^2 + 8^2\\
\ \\
z^2 = y^2 - 64\\
$$
Assim:
$$
z = \sqrt{y^2 - 64} \tag{8.2}
$$
Por semelhança entre os triângulos, temos que:
$$
\frac{r}{8} = \frac{y+8}{\sqrt{y^2-64}}
$$
Isolando $r$:
$$
r = \frac{8(y+8)}{\sqrt{y^2-64}} \tag{8.2}
$$
Elevamos ambos os membros ao quadrado para eliminar a raiz:
$$
r^2 = \frac{64(y+8)^2}{y^2-64}\\
\ \\
r^2 = \frac{64(y+8)(y+8)}{(y-8)(y+8)}
$$
Obtendo:
$$
r^2 = \frac{64(y+8)}{(y-8)} \tag{8.3}
$$
O volume de um cone é dado por:
$$
V = \frac{1}{3}\ \pi\ h\ r^2 \tag{8.4}
$$
Substituímos a altura $h=y+8$ e a relação $(8.3)$ na relação $(8.4)$:
$$
V = \frac{64\ \pi}{3} \cdot \frac{(y+8)^2}{(y-8)} \tag{8.5}
$$
A relação acima é uma função $V(y)$ e para calcularmos sua derivada devemos aplicar a regra para derivada de uma função quociente.
Lembrando que, se $f(x)=\cfrac{u}{v}$, então $f^\prime = \cfrac{u'v-v'u}{v^2}$. Assim:
$$
V^\prime = \frac{128\pi (y+8)\cdot 3(y-8)-64\pi (y+8)^2\cdot 3}{9(y-8)^2}\\
\ \\
V^\prime = \frac{128\pi(y+8)(y-8)-64\pi(y+8)^2}{3(y-8)^2}\\
\ \\
V^\prime = \frac{128\pi(y^2-64)-64\pi(y^2+16y+64)}{3(y-8)^2}\\
\ \\
V^\prime = 64\pi \left[ \frac{2(y^2-64)-(y^2+16y+64)}{3(y-8)^2} \right]\\
\ \\
V^\prime = 64\pi \left[ \frac{2y^2-128-y^2-16y-64}{3(y-8)^2} \right]\\
\ \\
V^\prime = 64\pi \left[ \frac{y^2 - 16y - 192}{3(y-8)^2} \right]
$$
Agora, podemos igualar a zero. Observe que o valor de $y$ deve ser diferente de $8$ e de $0$:
$$
64\pi \left[ \frac{y^2 - 16y - 192}{3(y-8)^2} \right] = 0 \tag{8.6}
$$
A relação $(8.6)$ nos fornece uma equação composta por uma razão entre duas equações. Mas como o denominador não deve ser igual a zero, nos resta que a equação gerada pelo numerador seja igual a zero. Neste caso, também descartamos $64\pi$, pois é uma constante. Assim, obtemos uma equação quadrática:
$$
y^2 - 16y -192 = 0\\
\ \\
y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\
\ \\
y = \frac{16 \pm \sqrt{256+768}}{2}\\
\ \\
y = \frac{16 \pm \sqrt{1024}}{2}\\
\ \\
y = \frac{16 \pm 32}{2}\\
\ \\
y_1 = 24\\
\ \\
y_2 = -8
$$
A raiz $y_2=-8$ não nos interessa, portanto tomamos $24$ como valor de $y$.
Para determinarmos as medidas do cone, tomamos sua altura, dada por:
$$
h = y + 8\\
\ \\
h = 24 + 8\\
\ \\
h = 32
$$
Agora, vamos determinar o raio da base do cone. Para isso, utilizamos o resultado obtido em $(8.2)$:
$$
r = \frac{8(24 + 8)}{\sqrt{24^2 -64}}\\
\ \\
r = \frac{256}{\sqrt{512}}\\
\ \\
r = \frac{2^8}{\sqrt{2^9}}\\
\ \\
r = 8\sqrt{2}
$$
As medidas do raio da base do cone e de sua altura são $r=8\sqrt{2}$ e $h=32$.
Referências:
- Notas de aula
Links para este artigo:
- https://bit.ly/-derivadas-maximos-minimos
- https://www.obaricentrodamente.com/2010/03/aplicacao-de-derivadas-para-determinacao-de-maximos-e-minimos.html






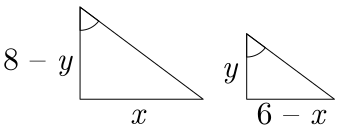



Muito bom o post e obrigado pelas citações.
ResponderExcluirExcelente. Como é fascinante o raciocinio matemático quando a teoria flui de forma tão clara como a apresentada.
ResponderExcluirObrigado amigo pelo comentário e pelo reconheciemnto do meu trabalho.
ResponderExcluirUm abraço!
Este comentário foi removido pelo autor.
ExcluirOlá Romário, veja este exemplo, só muda os valores:
Excluirhttp://br.answers.yahoo.com/question/index?qid=20110704171725AA4BPUj
Abraços.
Obrigado!
ExcluirNo seu primeiro exemplo você errou quando achou o valor do raio, pois era para ter dado 5 vezes raiz quadrada de 2 sobre RAIZ QUADRADA de 3, que racionalizando teremos 5 vezes raiz quadrada de 6 sobre 3.
ResponderExcluirAtt, Gustavo.
Verdade Gustavo. Corrigido. Obrigado por avisar. Um abraço!
ExcluirProfessor, antes de mais nada, muito obrigado por seu altruísmo de dividir conhecimento. Além de bastante claro, é um primor de didática.
ResponderExcluirCaro professor, estou com uma dúvida. No exemplo 4, no desenvolvimento (4.3), não seria A = (x2) / 4pi? Não estaria faltando a letra grega no denominador?
Desculpa se estou confundindo as coisas e fazendo perder seu tempo.
Abraço
Mauro
Olá Mauro, obrigado por seu comentário. Sua dúvida procede, pois realmente faltou o $\pi$ no denominador. Deve ter sido um erro de digitação, já que mais abaixo o $\pi$ volta... vou arrumar esta passagem.
ResponderExcluirUm abraço!
KLEBER, QUE BOAS ORIENTAÇÕES AMIGO......VOU TENTAR FAZER A PROVA DO PROFMAT PELA TERCEIRA VEZ.....O QUE FAÇO PARA PASSAR MEU AMIGO... SOU PROFESSOR DE MATEMÁTICA NO ENSINO MÉDIO......AQUI NA BAHIA......COLEGIO ESTADUAL......MAIS MINHA GRADUAÇÃO FOI A CONTINUADA APENAS 3 ANOS...LOGO TENHO DIFICULDADES EM DESAFIOS MATEMÁTICOS...E TAMBÉM TRABALHO COM MATEMÁTICA E FÍSICA...........UM GRANDE ABRAÇO
ResponderExcluirNo exemplo 6, como ficaria se um dos lados do retângulo fosse sobre a hipotenusa?
ResponderExcluirexelente post
ResponderExcluirMuito Bom..Parabéns!!!
ResponderExcluirEu queria que, se possível, você me ajudasse nessa questão Kleber:
ResponderExcluirDeve-se fazer uma caixa retangular com base quadrada e sem tampa. Achar o volume da máxima caixa que pode ser feita com 1200 pés quadrados de material.
Obrigado! (:
Matheus, veja a resolução na imagem neste link: http://img51.imageshack.us/img51/7263/dv5d.jpg
ExcluirPara o volume, multiplicar área da base pela altura, acho que ficou faltando na resolução...
Abraços.
Muito bom o post. Gostaria de saber o porquê de igualar a derivada à zero e a relação com aquela fórmula do Yvértice para calcular o máximo da área.
ResponderExcluirFlávio, Veja este comentário feito pelo Prof. Paulo Sérgio C. Lino:
ExcluirPrimeiramente tem que ficar claro que nem todos os problemas de otimização envolvem funções quadráticas e por isso, o conceito de derivada é adequado.
Antes de tudo, temos que definir o que é um ponto de máximo local e um ponto de mínimo local. Dizemos que um $P_0(x_0,f(x_0))$ sobre um gráfico de um função $f$ é um ponto de máximo local se $f(x) \leq f(x_0)$ para todo $x$ próximo ou numa vizinhança de $x_0$. A definição de ponto de mínimo local é análoga. E o que isso tem haver com derivadas? Aí surge o teorema de Fermat, que afirma que nos pontos de máximos e mínimos locais de uma função $f$, a derivada é nula. Por isso, que anulamos a derivada da função para encontrar tais pontos. Além disso, os pontos que anulam a derivada são chamados de pontos críticos. Nem todo ponto crítico é um ponto de máximo ou mínimo local, pois eles podem ser pontos de inflexão.
O valor do raio está errado, ao invés de 2 raiz de 2, é 8 raiz de 2.
ResponderExcluirPoderia me ajudar no esboço do desenho para desenvolver este exercício ... "Obtenha as dimensões da maior caixa fechada com base quadrada que pode ser construída com 12m² de papelão."...acredito que seja parecido com a questão 3.
ResponderExcluirProfessor, acredito que o gabarito da ultima questão, com relação ao raio do cone esteja equivocado. Sendo ele, 8 raiz de 2, e nçao 2 raíz de 2. grato pela atenção, e muito bom os exercícios!
ResponderExcluirCorretíssimo Maurício. Em breve farei a correção. Obrigado por relatar o erro.
ExcluirUm abraço!
Alguém consegue me ajudar com este problema.
ResponderExcluirUm metalúrgico foi contratado por uma fábrica de papel para projetar e construir um tanque retangular de aço, com base quadrada, sem tampa e com 108m³ de capacidade. O tanque será construído soldando-se chapas de aço umas às outras ao longo das bordas. Como engenheiro, sua tarefa é:
a) determinar as dimensões para a base e a altura que farão o tanque pesar o mínimo possível, considerando um único tipo de aço.
b) determinar as dimensões para a base e a altura que farão o tanque custar o mínimo possível, considerando que o preço do metro quadrado para a base será de R$ 202,00 e para as laterais será de R$ 186,00.
c) nas condições descritas no item “b”, quanto custará o tanque?
De onde saiu 96 do exemplo 3?
ResponderExcluirVem do produto notável:
Excluir$$(24-2x)^2 = 576 - 96x + 4x^2$$
Olá!
ExcluirSegue a regra:
a^2-2ab+b^2
como saber se vai maximizar ou minimizar a área, ao fazer a derivada?
ResponderExcluirEu fiz a mesma pergunta a meu professor quando aprendi na faculdade. Disse que, se montar a equação corretamente, ela já te leva à maximização ou à minimização, de acordo com o problema.
ExcluirValeu, Kleber, isso faz muito sentido, a forma como moldamos a equação determina se a derivada levará ao máximo ou mínimo, tive essa luz ontem após umas pesquisas no Google. Concluí, também, que na dúvida, vale apelar para a segunda derivada uma vez que ela denuncia a concavidade, por exemplo, no caso de uma equação quadrática.
Excluir"Igualamos a zero para obtermos uma equação que nos leva ao valor de máximo" Por que se iguala a zero qual a ideia disto? porque pelo que sei igualamos a eq. do 2º grau para obtermos os zeros ou raizes da função
ResponderExcluirOlá amigo.
ExcluirNão confunda igualar uma equação a zero para encontrar suas raízes com igualar uma derivada a zero para determinar os pontos de máximos e mínimos de uma função.
Quando uma função tem pontos de máximo ou mínimo, a primeira derivada é igual a zero nesse ponto, ou seja a reta tangente nesse ponto é paralela ao eixo dos x.