Volume de uma Calota Esférica

Para esta demonstração, podemos partir do mesmo princípio utilizado para o cálculo do Volume da Esfera, envolvendo o conceito de integral definida. Podemos adotar o mesmo raciocínio para encontrarmos a função $f (x)$ a ser integrada, alterando somente os limites de integração.

 

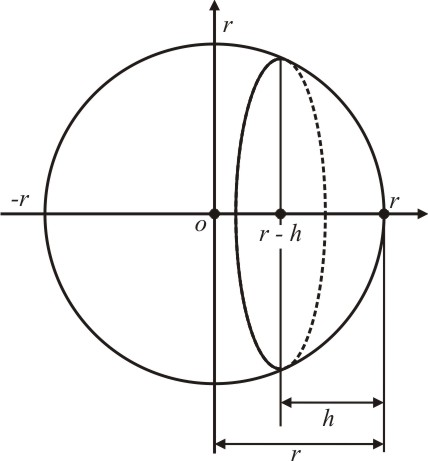
Primeiramente, vamos definir: Calota esférica é o sólido gerado a partir de uma esfera ao ser seccionada por um plano:

Figura 1

Desta forma, os limites de integração serão de $r – h$ até $r$.

Para simplificar este desenvolvimento, vamos partir da função $f (x)$, que foi originada da equação da circunferência de centro na origem:

$$
y = \sqrt{r^2-x^2} \tag{1}
$$

Veja o desenvolvimento completo acessando o link para o artigo: Volume da Esfera.

 

Vamos posicionar a figura 1 de outro modo, mais conveniente:

Figura 2

Suponha, agora, a calota esférica de altura $h$ formada por infinitos cilindros de alturas infinitesimais $dx$ e raios $y$, onde $y$ é variável para cada ponto de $h$:

Figura 3

Sabemos que o volume do cilindro é dado por:

$$
V_{cilindro} = A_b \cdot h\\
\ \\
V_{cilindro} = \pi\ y^2 \cdot h
$$

E, neste caso:

$$
V_{cilindro} = \pi\ y^2\ dx \tag{2}
$$

A soma destes infinitos cilindros de alturas infinitesimais forma a calota esférica, nos limites $r – h$ e $r$. Então, o seu volume será dado por:

$$
V = \int_{r-h}^{r} y^2\ dx
$$

Fatorando a constante:

$$
V = \pi \int_{r-h}^{r} y^2\ dx \tag{3}
$$

Substituímos a equação $(1)$ na integral $(3)$:

$$
V = \pi \int_{r-h}^r \left( \sqrt{r^2-x^2} \right)^2\ dx\\
\ \\
V = \pi \int_{r-h}^r \left( r^2 -x^2\right)\ dx
$$

Integrando em relação a $x$, obtemos:

$$
V = \pi \left[ r^2\ x - \frac{x^3}{3} \right]_{r-h}^{r}
$$

Aplicando os limites:

$$
V = \pi \left[ \left( r^2 r - \frac{r^3}{3} \right) - \left(r^2 (r-h) - \frac{(r-h)^3}{3}\right) \right]
$$

Agora é somente álgebra:

$$
V = \pi \left[ \left(r^3-\frac{r^3}{3}\right) - \left(r^3-r^2h-\frac{r^3-3r^2h+3rh^2-h^3}{3}\right)\right]\\
\ \\
V = \pi \left[ \left(\frac{3r^3-r^3}{3}\right) - \left(\frac{3r^3-3r^2h-r^3+3r^2h-3rh^2+h^3}{3}\right)\right]\\
\ \\
V = \frac{\pi}{3} \Big( 2r^3-3r^3+r^3+3rh^2-h^3 \Big)\\
\ \\
V = \frac{\pi}{3} \Big( 3rh^2-h^3 \Big)\\
$$

E por fim:

$$
V = \frac{1}{3}\ \pi\ h^2(3r-h)
$$

Links para este artigo:

• https://bit.ly/volume-calota-esferica
  
• https://www.obaricentrodamente.com/2010/09/volume-de-uma-calota-esferica.html

 

Veja mais:

• Volume da esfera
  
• Volume do anel esférico
  
• Volume do segmento esférico