Como determinar o ângulo interno de um polígono regular

Vamos construir um método para podermos determinar o ângulo interno de um polígono regular qualquer a partir de seu número de lados. Um método simples é decompor o polígono em triângulos, traçando diagonais a partir de um único vértice, pois sabemos que a soma dos ângulos internos de um triângulo qualquer é igual a $180°$ e assim fica mais fácil. Assim, podemos concluir que:

1) Para o polígono regular de 4 lados, o quadrado, podemos decompô-lo em 2 triângulos:

2) Para o polígono regular de 5 lados, o pentágono, podemos decompô-lo em 3 triângulos:

3) Para o polígono regular de 6 lados, o hexágono, podemos decompô-lo em 4 triângulos:

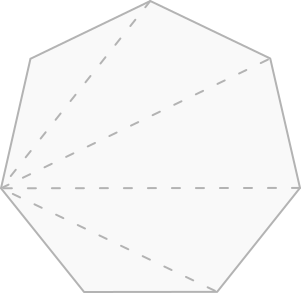
4) Para o polígono regular de 7 lados, o heptágono, podemos decompô-lo em 5 triângulos:

Vejam que há uma associação entre o número de lados do polígono e a quantidade de triângulos em que podemos decompô-lo. Assim, montamos a tabela:

Desta forma, encontramos a lei de formação e chegamos à conclusão que o número de triângulos $(T)$ formado pelas diagonais partindo de um único vértice é igual ao número de lados do polígono menos 2:

$$
T = n-2
$$

Para o quadrado, onde podemos dividi-lo em dois triângulos, temos que a soma dos ângulos internos será de $180° + 180° = 360°$:

E o ângulo interno formado por cada vértice será dado pela divisão de $360°$ pelo número de lados do polígono:

$$
\frac{360°}{4} = 90°
$$

Seguindo o mesmo raciocínio para outros polígonos regulares, chegamos à fórmula:

$$
\alpha = \frac{T \cdot 180°}{n}
$$

Onde $\alpha$ é o ângulo interno de cada vértice, $T$ é o número de triângulos em que o polígono pode ser decomposto e $n$ é o número de lados deste polígono. Mas $T = n – 2$ , logo:

$$
\alpha = \frac{180° \cdot (n-2)}{n}
$$

Construímos então uma tabela onde se relaciona o número de lados de um polígono com o ângulo interno de cada vértice:

Vejam que quanto o número de lados de um polígono cresce, tendendo ao infinito, mais perto de $180°$ é o ângulo interno dos vértices. Isso quer dizer que, se ampliarmos um dos vértices veremos os segmentos que formam o ângulo alfa tendendo a uma reta.

Links para este artigo:

• https://bit.ly/angulo-interno-poligono
  
• http://www.obaricentrodamente.com/2011/07/como-determinar-o-angulo-interno-de-um.html
  

Veja mais:

• Como determinar o número de diagonais de um polígono convexo de n lados
• Soma dos ângulos internos e externos de um polígono convexo
  
• Como calcular a distância entre dois pontos no plano