Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível.
Considere um raio de luz que parte de um ponto $A$ e segue a um ponto $P$ sobre um espelho plano sendo refletido e passando por um ponto $B$. O raio incidente e o raio refletido possuem ângulos iguais a $\alpha$ e $\beta$, respectivamente.
Suponha que o raio de luz siga o caminho mais curto de $A$ a $B$ passando pelo espelho. Provemos que essa lei de reflexão seguindo o caminho $APB$ é mais curto quando $\alpha = \beta$.

[Figura 1]
Considere que o ponto $P$ assuma várias posições no espelho, sendo cada posição determinada por um valor de $x$, conforme se pode observar na figura acima. Vamos considerar o comprimento $L$ do percurso do raio de luz como sendo uma função de $x$. Assim, podemos escrever a seguinte expressão:
\begin{equation*}L = \sqrt{a^2+x^2} + \sqrt{b^2+(c-x)^2} = (a^2+x^2)^{1/2} + \left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
A derivada desta expressão nos leva a:
\begin{equation*}
\frac{dL}{dx} = \frac{1}{2} \left(a^2+x^2\right)^{-1/2} \cdot (2x)+\frac{1}{2}\left[ b^2+(c-x)^2 \right]^{-1/2} \cdot 2(c-x)(-1)
\end{equation*}
\begin{equation}
\frac{dL}{dx} = \frac{x}{\sqrt{a^2+x^2}} - \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Minimizamos o comprimento $L$ igualando a deriva acima a zero, obtendo:
\begin{equation}\frac{x}{\sqrt{a^2+x^2}} = \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Esta equação nos revela que para os ângulos $\alpha$ e $\beta$ nos dois triângulos retângulos da figura acima, as razões entre a hipotenusa e o lado adjacente são iguais e assim $\alpha$ e $\beta$ são iguais.
Derivando a função $L(x)$ e em seguida igualando a zero, minimizamos o comprimento $L$. Podemos ainda utilizar a relação dada em $(1)$ no teste da segunda derivada:
\begin{equation*}\frac{d^2L}{dx^2} = \frac{a^2}{(a^2+x^2)^{3/2}} + \frac{b^2}{\left[b^2+(c-x)^2 \right]^{3/2}}
\end{equation*}
Basta observar que a quantidade acima será positiva, já que $a$, $b$ e $c$ são distâncias entre pontos.
Podemos ainda utilizar a trigonometria nos triângulos retângulos da figura acima, de modo que a condição de minimização dada em $(2)$ pode ser escrita como:
\begin{equation*}\cos(\alpha) = \cos(\beta)
\end{equation*}
O que nos leva a $\alpha = \beta$.
Esta lei de reflexão já era conhecida pelos gregos da Antiguidade, mas o fato de que o raio de luz refletido segue o caminho mais curto foi descoberto muito mais tarde por Heron de Alexandria, no século $I~d.C.$.
A demonstração de Heron é simples, porém engenhosa: sejam $A$ e $B$ os mesmos pontos da figura anterior, reproduzidos na figura abaixo, e seja $B~^\prime$ a imagem especular de $B$. A superfície do espelho é o plano bissetor de $BB~^\prime$. O segmento $AB~^\prime$ intercepta o espelho num ponto $P$ e este é o ponto onde o raio de luz é refletido ao passar de $A$ para $B$, pois então $\alpha = \gamma$ e $\gamma = \beta$ e assim $\alpha = \beta$. O percurso total do raio de luz é dado por:
\begin{equation*}AP + PB = AP + PB~^\prime = AB~^\prime
\end{equation*}
O percurso de $A$ a $B$, passando por qualquer outro ponto $P~^\prime$ do espelho é:
\begin{equation*}AP~^\prime + P~^\prime B = AP~^\prime + P~^\prime B~^\prime
\end{equation*}
que é maior do que o terceiro lado do triângulo $AP~^\prime B~^\prime$, o lado $AB~^\prime $, o que mostra que o percurso real de $A$ para $B$ do raio de luz refletido no espelho é o menor possível.

[Figura 2]
Temos que deixar claro que estes cálculos só tem sentido se considerarmos que o raio de luz tem todo o percurso em um único meio a uma velocidade constante. No entanto, em meios diferentes, como ar, água, vidro, a luz tem velocidades diferentes. Se um raio de luz passa do ar para a água, ele é refratado passando a uma direção mais próxima da perpendicular à interface. O percurso $APB$ não é mais o caminho mais curto de $A$ a $B$.
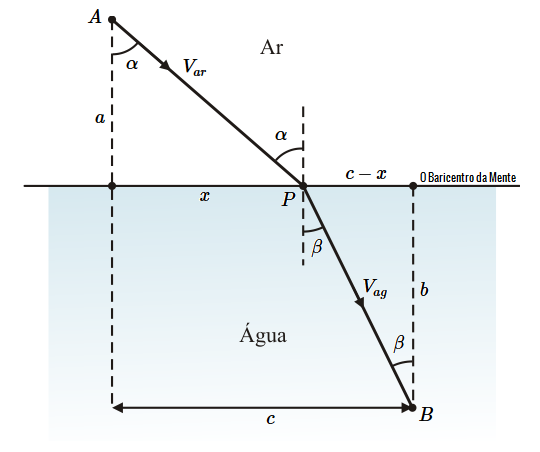
[Figura 3]
Em $1621$ o cientista holandês Snell descobriu empiricamente que o caminho real do raio de luz é o que satisfaz a equação:
\begin{equation}\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \text{constante}
\end{equation}
onde essa constante é independente da posição de $A$ e $B$. Esse fato é chamado de Lei de Refração de Snell. Podemos provar a Lei de Snell partindo do pressuposto de que o raio percorre um caminho de $A$ a $B$ de modo a minimizar o tempo total de percurso.
Seja a velocidade da luz no ar denotada por $V_{ar}$ e na água $V_{ag}$ e seja $T$ o tempo total do percurso, tempo no ar mais o tempo na água:
\begin{equation*}T = \frac{\sqrt{a^2+x^2}}{V_{ar}} + \frac{\sqrt{b^2+(c-x)^2}}{V_{ag}}\\
\ \\
T = \frac{1}{V_{ar}}\left(a^2+x^2\right)^{1/2} + \frac{1}{V_{ag}}\left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
Se calcularmos a derivada desta função $T(x)$ e observarmos o seu significado em termos da figura acima, obteremos:
\begin{equation*}\small \frac{dT}{dx} = \frac{1}{V_{ar}} \cdot \frac{1}{2}\cdot \left(a^2+x^2\right)^{-1/2} \cdot 2x + \frac{1}{V_{ag}}\cdot \frac{1}{2}\cdot \left( b^2+(c-x)^2 \right)^{-1/2} \cdot 2(c-x)\cdot (-1)\\
\end{equation*}
\begin{equation}
\frac{dT}{dx} = \frac{1}{V_{ar}}\cdot\frac{x}{\sqrt{a^2+x^2}} - \frac{1}{V_{ag}}\cdot \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
E ainda pela figura acima, temos:
\begin{equation*}
\text{sen}(\alpha) = \frac{x}{\sqrt{a^2+x^2}} \quad \text{e} \quad \text{sen}(\beta)=\frac{c-x}{\sqrt{b^2(c-x)^2}}
\end{equation*}
Substituindo na derivada anterior, obtemos:
\begin{equation*}
\frac{dT}{dx} = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Para obtermos o $T$ mínimo, igualamos essa derivada a zero:
\begin{equation*}
0 = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}\\
\ \\
\frac{\text{sen}(\alpha)}{V_{ar}} = \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Ou ainda:
\begin{equation}
\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \frac{V_{ar}}{V_{ag}}
\end{equation}
Esta é a forma mais reveladora da Lei de Snell porque dá um significado físico da constante que aparece em $(3)$, pois é a razão entre a velocidade da luz no ar e a velocidade (menor) da luz na água. Essa constante é chamada de índice de refração da água. Se substituirmos a água por qualquer outro meio translúcido, como álcool, glicerina, vidro, ... então a constante terá um valor numérico diferente, pois cada meio possui um índice de refração diferente.
Podemos aplicar o teste da segunda derivada em $(4)$ para verificar se $(5)$ realmente minimiza $T$, observando se esta é positiva:
\begin{equation*}\frac{d^2T}{dx^2} = \frac{1}{V_{ar}}\frac{a^2}{(a^2+x^2)^{3/2}} + \frac{1}{V_{ag}}\frac{b^2}{\left( b^2+(c-x)^2 \right)^{3/2}}>0
\end{equation*}
Links para este artigo:
- http://bit.ly/derivadas-reflexao-refracao
- https://www.obaricentrodamente.com/2016/07/aplicacao-de-derivadas-no-estudo-sobre-a-reflexao-e-refracao-de-um-raio-de-luz.html
Referências:
- Cálculo com Geometria Analítica - Simmons - Ed. McGraw-Hill
Veja mais:
- O refinamento de Snell
- Usando derivadas para aproximar funções
- Aplicação de derivadas para determinação de máximos e mínimos


Olá, Kleber.
ResponderExcluirA saída, no caso da refração, foi igualar a zero a derivada do tempo em função de x. Na verdade, impõe-se aí uma condição para o valor de tempo mínimo. Se formos generalizar para todos os casos (reflexão e refração) físicamente, isto significaria que a luz procura sempre percorrer o caminho em que o tempo de percurso é mínimo. Seria isso Kleber? Se sim, no caso da reflexão, poderíamos impor a mesma condição de tempo mínimo, e neste caso, como a velocidade não se altera (pois não há mudança de meios) chegaríamos às mesmas conclusões sobre a igualdade entre os ângulos de incidência e de reflexão.
Interessante é que,como o post revela, Snell chegou a estas relações de seno e cosseno de forma empírica.
Todos os professores, quando ensinam aos alunos do ensino médio as leis da reflexão, explicam alguns conceitos básicos, como esse da igualdade entre os ângulos, na refração, passamos a fórmula (Lei de Snell-Descartes) os alunos aceitam, decoram e seguimos com os cálculos. Nunca imaginei que esses mesmos conceitos pudessem ser demonstrados, estabelecendo esta condição de tempo mínimo de trajeto da luz. Muito interessante. Fiquei imaginando: Será que na Teoria da Relatividade, este conceito de tempo mínimo para um percurso da luz também é seguido? Não sei se seria tão simples. Parabéns pelo achado destas demonstrações e pela publicação delas aqui. Abraço, amigo.
Olá Jairo.
ExcluirNa reflexão, foi encontrada uma função $L(x)$ e depois de encontrar sua derivada, foi igualada a zero para obtermos o valor mínimo de $L$, o que levou à igualdade dos ângulos. Na refração, Foi encontrada uma função $T(x)$ e depois de derivada e igualada a zero, obteve-se uma relação entre os senos dos ângulos e as velocidades da luz na água e no ar. Equação $(5)$. Se as velocidades fossem iguais, na água e no ar, então os ângulos seriam iguais.
Incrível como os antigos resolviam tais problemas, com o mínimo de conhecimento e matemática retórica.
Uma coisa que aprendi neste tempo em que estudo matemática é que a natureza minimiza esforços. O Cálculo ajuda a entender como isso funciona.
Não conheço muito sobre a Teoria da Relatividade e prefiro não opinar, mas se tua intuição diz que não seria tão simples assim, possivelmente não é mesmo.
Agradeço pelo comentário sempre crítico. Um grande abraço!
Muito bom!
ResponderExcluirNão tinha visto ainda uma dedução da Lei de Snell.
Desculpe a pergunta trivial, mas porque para minimizar L a derivada dL/dX precisa ser zero?
ResponderExcluirEstou há anos sem ver isso... tem relação com máximos e mínimos relativos passarem por pontos de deflexão e por isso a tangente ser zero nesses pontos? Se for isso tanto para maximizar como para minimizar devemos igualar a derivada a zero?
ResponderExcluirOlá Carlos. Exatamente. Como a derivada de uma função é a reta tangente num ponto x, se x for num ponto de inflexão da curva, a inclinação será zero, ou seja paralela ao eixo dos x, acima ou abaixo. Então, igualamos a zero para encontrarmos o valor de máximo (acima do eixo dos x) ou o valor de mínimo (abaixo do eixo dos x).
ExcluirAbraços!