Lembra daquelas tabelas de integrais? Quando estudamos em nossa graduação, muitas vezes somente consultamos as tabelas e tomamos o resultado. Mas como esses resultados foram obtidos?
Este artigo faz parte de uma série de resoluções de integrais que venho fazendo para demonstrar os resultados que encontramos nessas tabelas.
Primeiramente a integral é resolvida passo-a-passo e em seguida é aplicada em exemplos. Para cada integral, utiliza-se técnicas específicas para sua resolução, que pode ser por substituição, por partes, por frações parciais ou substituição trigonométrica.
Este artigo faz parte de uma série de resoluções de integrais que venho fazendo para demonstrar os resultados que encontramos nessas tabelas.
Primeiramente a integral é resolvida passo-a-passo e em seguida é aplicada em exemplos. Para cada integral, utiliza-se técnicas específicas para sua resolução, que pode ser por substituição, por partes, por frações parciais ou substituição trigonométrica.
Nesta postagem, vamos demonstrar que:
$$\int \ln(ax+b)\ dx = \left( \frac{b}{a}+x \right) \ln(ax+b) -x + C
$$
sendo $a$ e $b$ constantes, com $a \neq 0$ e $ax+b>0$.
Seja a integral:
$$I = \int \ln(ax+b)\ dx
$$
Para o integrando $\ln(ax+b)$, fazemos a substituição $z=ax+b$. Assim, $dz=a\ dx$ e $\displaystyle dx=\frac{1}{a} dz$:
$$I = \frac{1}{a} \int\ln(z)\ dz
$$
Para o integrando $\ln(z)$, utilizamos o método de integração por partes. Lembrando que:
$$\int u\ dv = uv - \int v\ du \tag{1}
$$
Desta forma, fazemos $u=\ln(z)$ e $dv=dz$, para obtermos $\displaystyle du=\frac{1}{z}\ dz$ e $v=z$.
$$\int u\ dv = z\ln(z) - \int z \cdot \frac{1}{z}\ dz\\
\ \\
\int u\ dv = z\ln(z) - \int dz
$$
Voltando à integral $I$:
$$I = \frac{1}{a} \left[ z\ln(z)-\int dz \right]\\
\ \\
I = \frac{z\ln(z)}{a}-\frac{z}{a}+C
$$
Mas, $z=ax+b$, logo:
$$I = \frac{(ax+b)\ln(ax+b)}{a} - \frac{(ax+b)}{a}+C\\
\ \\
I = \frac{(ax+b)\left(\ln(ax+b)-1\right)}{a}+C\\
\ \\
I = \left(\frac{ax+b}{a}\right) \left(\ln(ax+b)-1\right)+C\\
\ \\
I = \left( \frac{b}{a}+x \right) \ln(ax+b) - \left(\frac{b}{a}+x\right)+C\\
\ \\
I = \left( \frac{b}{a}+x \right) \ln(ax+b) - x + \left(C-\frac{b}{a}\right)\\
\ \\
I = \left( \frac{b}{a}+x \right) \ln(ax+b)-x+C
$$
Exemplo:
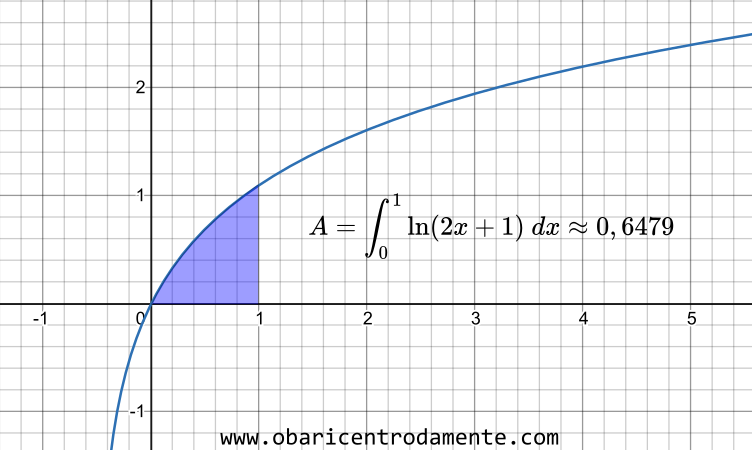
Vamos calcular a área sob a curva $f(x)=\ln(2x+1)$, no intervalo de $x=0$ a $x=1$.
Para calcularmos a área sob a curva $f(x)$, utilizamos o conceito de integral definida:
$$A = \int_0^1 \ln(2x+1)\ dx
$$
Utilizando o resultado obtido anteriormente, fazemos $a=2$ e $b=1$:
$$A = \left[ \left(\frac{1}{2}+x\right) \ln(2x+1)-x \right]_0^1\\
\ \\
A = \left[ \left(\frac{1}{2}+1\right)\ln(3)-1 \right] - \left[ \left(\frac{1}{2}\right)\ln(1)\right]\\
\ \\
A = \left[ \frac{3}{2} \ln(3)-1\right]\\
\ \\
A \approx 0,6479
$$
Assim, a área desejada vale aproximadamente $0,6479$ unidades de área.



Postar um comentário