Neste artigo veremos como calcular distâncias no espaço utilizando a Geometria Analítica. Podemos ter as seguintes situações:
- Ponto — Ponto
- Ponto — Reta
- Reta — Reta
- Ponto — Plano
- Plano — Plano
- Reta — Plano
1) Distância entre dois pontos
Iniciamos fixando um sistema ortogonal $\left ( O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k} \right )$ de coordenadas.
Sejam dois pontos $P_1 (x_1, y_1, z_1)$ e $P_2 (x_2, y_2, z_2)$. A distância $d$ entre esses pontos é o módulo do vetor $\overrightarrow{P_1P_2}$:
$$d(P_1P_2) = \left \| \overrightarrow{P_1P_2}\right \|
$$
Logo:
$$d(P_1P_2) = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2} \tag{1.1}
$$
Exemplo 1:
Vamos calcular a distância entre os pontos $P_1(7,3,4)$ e $P_2(1,0,6)$.
Temos que:
- $x_1 = 7$ e $x_2 = 1$
- $y_1 = 3$ e $y_2 = 0$
- $z_1 = 4$ e $z_2 = 6$
Aplicando estes valores na fórmula para distância entre dois pontos, dada em $(1.1)$, obtemos:
$$d(P_1P_2) = \sqrt{(1-7)^2 + (0-3)^2 + (6-4)^2}\\
\ \\
d(P_1P_2) = \sqrt{36 + 9 + 4}\\
\ \\
d(P_1P_2) = \sqrt{49}\\
\ \\
d(P_1P_2) = 7\ u.c.
$$
Assim, a distância entre os pontos $P_1$ e $P_2$ mede 7 unidades de comprimento.
Exemplo 2:
Dados os pontos $P_1(0,2,z_1)$ e $P_2(-2, 0, 1)$, calcular $z_1$ sabendo que $d(P_1P_2) = 3$.
$$d(P_1P_2) = \sqrt{(-2-0)^2 + (0-2)^2 + ( 1-z_1)^2}\\
\ \\
3 = \sqrt{4 + 4 + (1-z_1)^2}\\
\ \\
3 = \sqrt{8 + 1 - 2z_1 + z_1^2}
$$
Elevamos ambos os membros da equação ao quadrado para eliminarmos a raiz quadrada:
$$9 = 9 - 2z_1 + z_1^2\\
\ \\
z_1^2 -2z_1 = 0\\
\ \\
z_1 (z_1 -2) = 0
$$
Daqui resulta que ou $z_1 = 0$ ou $z_1 = 2$.
2) Distância de um ponto a uma reta
Seja uma reta $r$ definida por um ponto $P_1(x_1,y_1,z_1)$ e por um vetor $\overrightarrow{v}=(a,b,c)$. Dado um ponto $P_0(x_0,y_0,z_0)$ qualquer no espaço, os vetores $\overrightarrow{v}$ e $\overrightarrow{P_1P_0}$ determinam um paralelogramo cuja altura corresponde à distância $d$ entre $P_0$ à reta $r$:
A área $A$ de um paralelogramo é dada pelo produto da base pela altura:
$$A=\left \| \overrightarrow{v}\right \|d \tag{2.1}
$$
E utilizando a interpretação geométrica do módulo do produto vetorial:
$$A=\left \| \overrightarrow{v} \times \overrightarrow{P_1P_0} \right \| \tag{2.2}
$$
Igualando $(2.1)$ e $(2.2)$:
$$\left \| \overrightarrow{v}\right \|d = \left \| \overrightarrow{v} \times \overrightarrow{P_1P_0} \right \|\\
$$
Isolando $d$:
$$d = \frac{\left \| \overrightarrow{v} \times \overrightarrow{P_1P_0} \right \|}{\left \| \overrightarrow{v}\right \|} \tag{2.3}
$$
Exemplo 3:
Vamos calcular a distância entre o ponto $P_0(2,0,7)$ à reta $\displaystyle r:\ \frac{x}{2} = \frac{y-2}{2} = \frac{z+3}{1}$.
A reta $r$ passa pelo ponto $P_1(0,2,-3)$ e tem direção do vetor $\overrightarrow{v} = (2,2,1)$. O vetor $\overrightarrow{P_1P_0}=P_0-P_1=(2,-2,10)$. Assim:
$$d(P_0,r) = \frac{\left \| (2,2,1) \times (2,-2,10) \right \|}{\left \| (2,2,1) \right \|}
$$
Vamos calcular o produto vetorial entre os vetores $\overrightarrow{v}$ e $\overrightarrow{P_1P_0}$:
$$\overrightarrow{v} \times \overrightarrow{P_1P_0} = (2,2,1)\times(2,-2,10)
$$
$$
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
2 & 2 & 1\\
2 & -2 & 10
\end{vmatrix}
\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
2 & 2 & 1\\
2 & -2 & 10
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
2 & 2\\
2 & -2
\end{matrix}\right|
$$
\overrightarrow{v} \times \overrightarrow{P_1P_0} = 20\vec{i}+2\vec{j}-4\vec{k}-4\vec{k}+2\vec{i}-20\vec{j}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = 22\vec{i}-18\vec{j}-8\vec{k}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = (22,-18,-8)
$$
d(P_0,r)= \frac{\left \| (22,-18,-8) \right \|}{\left \| (2,2,1) \right \|}\\
\ \\
d(P_0,r)= \frac{\sqrt{22^2+(-18)^2+(-8)^2}}{\sqrt{2^2+2^2+4^2}}\\
\ \\
d(P_0,r)= \frac{\sqrt{484+324+64}}{\sqrt{4+4+1}}\\
\ \\
d(P_0,r)= \frac{\sqrt{872}}{3} \ u.c.
$$
d(r,s) = d(P_0,s),\quad P_0 \in r
$$
ou ainda:
$$
d(r,s) = r(P_0,r), \quad P_0 \in s
$$
x = \frac{y-3}{-2} = \frac{z}{2}
$$
(2,4,-4) = 2(1,-2,2)
$$
d(P_0,s) = \frac{\left \| \overrightarrow{v} \times \overrightarrow{P_1P_0} \right \|}{\left \| \overrightarrow{v} \right \|}
$$
d(P_0,s) = \frac{\left \| (-2,4,-4) \times (1,2,3) \right \|}{\left \| (-2,4,-4) \right \|}
$$
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
-2 & 4 & -4\\
1 & 2 & 3
\end{vmatrix}
\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
-2 & 4 & -4\\
1 & 2 & 3
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
-2 & 4\\
1 & 2
\end{matrix}\right|
$$
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
2 & 2 & 1\\
2 & -2 & 10
\end{vmatrix}
\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
2 & 2 & 1\\
2 & -2 & 10
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
2 & 2\\
2 & -2
\end{matrix}\right|
$$
Somamos os produtos das diagonais principais e subtraímos a soma dos produtos das diagonais secundárias:
$$\overrightarrow{v} \times \overrightarrow{P_1P_0} = 20\vec{i}+2\vec{j}-4\vec{k}-4\vec{k}+2\vec{i}-20\vec{j}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = 22\vec{i}-18\vec{j}-8\vec{k}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = (22,-18,-8)
$$
Assim, temos que:
$$d(P_0,r)= \frac{\left \| (22,-18,-8) \right \|}{\left \| (2,2,1) \right \|}\\
\ \\
d(P_0,r)= \frac{\sqrt{22^2+(-18)^2+(-8)^2}}{\sqrt{2^2+2^2+4^2}}\\
\ \\
d(P_0,r)= \frac{\sqrt{484+324+64}}{\sqrt{4+4+1}}\\
\ \\
d(P_0,r)= \frac{\sqrt{872}}{3} \ u.c.
$$
Assim, a distância entre o ponto $P_0$ e a reta $r$ mede $\displaystyle \frac{2\sqrt{218}}{3}$ unidades de comprimento.
3) Distância entre duas retas
Em relação a duas retas no espaço, podemos ter as possibilidades: as retas são concorrentes, as retas são paralelas ou as retas são reversas.
3.1) As retas são concorrentes
A distância entre duas retas $r$ e $s$ concorrentes é nula por definição, pois estas se cruzam em um único ponto onde $d(P_1,P_2)=0$ e, consequentemente $d(r,s)=0$.
Lembrando que retas concorrentes são aquelas que possuem apenas um ponto em comum.
3.2) As retas são paralelas
A distância $d$ entre duas retas paralelas $r$ e $s$ é a distância de um ponto qualquer $P_0$ de uma delas à outra:
$$d(r,s) = d(P_0,s),\quad P_0 \in r
$$
ou ainda:
$$
d(r,s) = r(P_0,r), \quad P_0 \in s
$$
Deste modo, a distância entre duas retas paralelas se reduz ao cálculo da distância de um ponto a uma reta, visto no tópico anterior.
Exemplo 4:
Vamos calcular a distância entre as retas $r$ e $s$ dadas por:
$$
r: \left\{\begin{matrix}
y & = & - & 2x & + & 3\\
\ \\
z & = & & 2x & &
\end{matrix}\right.
$$
s: \left\{\begin{matrix}
x & = & - & 1 & - & 2t\\
y & = & & 1 & + & 4t\\
z & = & - & 3 & - & 4t
\end{matrix}\right.
$$
r: \left\{\begin{matrix}
y & = & - & 2x & + & 3\\
\ \\
z & = & & 2x & &
\end{matrix}\right.
$$
e
$$s: \left\{\begin{matrix}
x & = & - & 1 & - & 2t\\
y & = & & 1 & + & 4t\\
z & = & - & 3 & - & 4t
\end{matrix}\right.
$$
Para encontrar um vetor diretor da reta $r$, em sua forma reduzida, devemos reescrevê-la na forma simétrica e tomar os denominadores como componentes do vetor. Isolamos o $x$ em cada uma das equações e depois igualamos:
- $y = -2x+3 \Longrightarrow 2x = -y+3 \Longrightarrow \displaystyle x = \frac{y-3}{-2}$
- $z = 2x \Longrightarrow \displaystyle x = \frac{z}{2}$
Fazemos:
$$x = \frac{y-3}{-2} = \frac{z}{2}
$$
Assim, o vetor diretor $\overrightarrow{u}$ da reta $r$ é:
$$
\overrightarrow{u} = (1, -2, 2)
$$
\overrightarrow{u} = (1, -2, 2)
$$
Um vetor diretor da reta $s$, em sua forma paramétrica, são os coeficientes de $t$. Assim:
$$
\overrightarrow{v} = (-2, 4, -4)
$$
\overrightarrow{v} = (-2, 4, -4)
$$
Como podemos ver, as retas $r$ e $s$ realmente são paralelas, pois $\overrightarrow{v} = -2\overrightarrow{u}$:
$$(2,4,-4) = 2(1,-2,2)
$$
Calculamos a distância entre $r$ e $s$ por $d(r,s)=d(P_0,s)$, sendo $P_0 \in r$.
Vamos primeiramente encontrar um ponto pertencente a $r$. Fazemos $x=0$ e substituímos nas equações reduzidas de $r$, obtendo $y=3$ e $z=0$. Assim, temos que $P_0(0,3,0)$ é um ponto de $r$. A reta $s$ passa pelo ponto $P_1(-1,1,-3)$ e tem direção de $\overrightarrow{v}=(-2,4,-4)$.
Agora, podemos aplicar a fórmula para distância de um ponto a uma reta:
$$d(P_0,s) = \frac{\left \| \overrightarrow{v} \times \overrightarrow{P_1P_0} \right \|}{\left \| \overrightarrow{v} \right \|}
$$
Como $\overrightarrow{P_1P_0} = (1,2,3)$, temos:
$$d(P_0,s) = \frac{\left \| (-2,4,-4) \times (1,2,3) \right \|}{\left \| (-2,4,-4) \right \|}
$$
Calculamos o produto vetorial entre os vetores $(-2,4,-4)$ e $(1,2,3)$:
$$\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
-2 & 4 & -4\\
1 & 2 & 3
\end{vmatrix}
\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
-2 & 4 & -4\\
1 & 2 & 3
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
-2 & 4\\
1 & 2
\end{matrix}\right|
$$
Somamos os produtos das diagonais principais e subtraímos a soma dos produtos das diagonais secundárias:
$$\overrightarrow{v} \times \overrightarrow{P_1P_0} = 12\vec{i}-4\vec{j}-4\vec{k}-4\vec{k}+8\vec{i}+6\vec{j}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = 20\vec{i}+2\vec{j}-8\vec{k}\\
\ \\
\overrightarrow{v} \times \overrightarrow{P_1P_0} = (20,2,-8)
$$
Assim, temos que:
$$d(P_0,s) = \frac{\left \| (20,2,-8) \right \|}{\left \| (-2,4,-4) \right \|}\\
\ \\
d(P_0,s) = \frac{\sqrt{20^2+2^2+(-8)^2}}{\sqrt{(-2)^2+4^2+(-4)^2}}\\
\ \\
d(P_0,s) = \frac{\sqrt{400+4+64}}{\sqrt{4+16+16}}\\
\ \\
d(P_0,s) = \frac{\sqrt{468}}{\sqrt{36}}\\
\ \\
d(P_0,s) = \frac{6\sqrt{13}}{6}\\
\ \\
d(P_0,s) = \sqrt{13} u.c.
$$
Assim, a distância entre as retas $r$ e $s$ mede $\sqrt{13}$ unidades de comprimento.
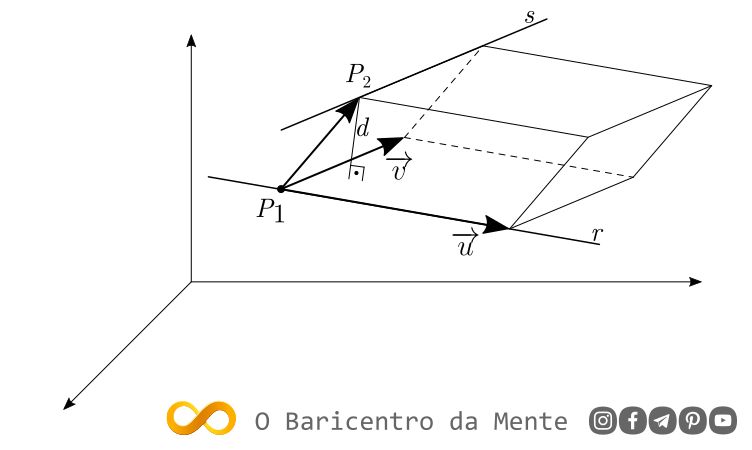
3.3) As retas são reversas
Retas reversas são aquelas que não possuem intersecção e não são paralelas, isso quer dizer que estão em planos diferentes.
Sejam duas retas reversas $r$ e $s$, onde a reta $r$ é definida po um ponto $P_1(x_1,y_1, z_1)$ e paralela ao vetor $\overrightarrow{u}=(a_1,b_1,c_1)$ e a reta $s$ é definida por um ponto $P_2(x_2,y_2,z_2)$ paralela ao vetor $\overrightarrow{v}=(a_2,b_2,c_2)$.
Os vetores $\overrightarrow{u}$, $\overrightarrow{v}$ e $\overrightarrow{P_1P_2}=(x_2-x_1,y_2-y_1,z_2-z_1)$ determinam um paralelepípedo, onde a base é definida pelos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ e a altura corresponde à distância $d$ entre as retas $r$ e $s$, uma vez que a reta $s$ é paralela ao plano da base:
O volume $V$ de um paralelepípedo é dado pelo produto da área da base pela altura:
$$V = \left \| \overrightarrow{u} \times \overrightarrow{v} \right \| d \tag{3.3.1}
$$
Pela interpretação geométrica do módulo o produto misto, temos:
$$V = \left \| \left(\overrightarrow{u} , \overrightarrow{v}, \overrightarrow{P_1P2}\right) \right \| \tag{3.3.2}
$$
Comparando as duas últimas equações:
$$\left \| \overrightarrow{u}\times \overrightarrow{v} \right \|d = \left \| (\overrightarrow{u} , \overrightarrow{v}, \overrightarrow{P_1P2}) \right \|
$$
O que nos leva a:
$$d = \frac{\left \| (\overrightarrow{u} , \overrightarrow{v}, \overrightarrow{P_1P2}) \right \|}{\left \| \overrightarrow{u}\times \overrightarrow{v} \right \|} \tag{3.3.3}
$$
Exemplo 5:
Vamos calcular a distância entre as retas $r$ e $s$ dadas por:
$$
r: \left\{\begin{matrix}
& & y & = & 1\\
\ \\
x & + & 2 & = & \displaystyle \frac{z-4}{-2}
\end{matrix}\right.
$$
s: \left\{\begin{matrix}
x & = & & 3 & & \\
y & = & & 2t & - & 1\\
z & = & - & t & + & 3
\end{matrix}\right.
$$
r: \left\{\begin{matrix}
& & y & = & 1\\
\ \\
x & + & 2 & = & \displaystyle \frac{z-4}{-2}
\end{matrix}\right.
$$
e
$$s: \left\{\begin{matrix}
x & = & & 3 & & \\
y & = & & 2t & - & 1\\
z & = & - & t & + & 3
\end{matrix}\right.
$$
Vamos encontrar um ponto $P_1$ onde passa a reta $r$:
Se tomarmos $x=-2$ e substituirmos na segunda equação reduzida de $r$:
$$
x+2 = \frac{z-4}{-2}\\
\ \\
-2+2 = \frac{z-4}{-2}\\
\ \\
0 = \frac{z-4}{-2}\\
\ \\
z = 4
$$E o vetor diretor $\overrightarrow{u}$ da reta $r$ pode ser obtido isolando o $x$ nas equações reduzidas e tomando seus denominadores como componentes do vetor:
$$x+2 = \frac{z-4}{-2}\\
\ \\
-2+2 = \frac{z-4}{-2}\\
\ \\
0 = \frac{z-4}{-2}\\
\ \\
z = 4
$$E o vetor diretor $\overrightarrow{u}$ da reta $r$ pode ser obtido isolando o $x$ nas equações reduzidas e tomando seus denominadores como componentes do vetor:
x+2 = \frac{z-4}{-2}\\
\ \\
x = \frac{z-4}{-2} - 2\\
\ \\
x = \frac{z}{-2}
$$
Assim, temos que $\overrightarrow{u}=(1,0,-2)$.
A reta $s$ passa pelo ponto $P_2(3,-1,3)$ e tem a direção do vetor $\overrightarrow{v}=(0,2,-1)$.
O vetor $\overrightarrow{P_1P_2} = (P_2-P_1) = (5,-2,-1)$.
Primeiro calculamos o produto misto:
$$\left (\overrightarrow{u},\overrightarrow{v}, \overrightarrow{P_1P_0} \right ) =
\begin{vmatrix}
1 & 0 & -2\\
0 & 2 & -1\\
5 & -2 & -1
\end{vmatrix}
\\
\ \\
\left (\overrightarrow{u},\overrightarrow{v}, \overrightarrow{P_1P_0} \right ) =
\begin{vmatrix}
1 & 0 & -2\\
0 & 2 & -1\\
5 & -2 & -1
\end{vmatrix}
\left.\begin{matrix}
1 & 0 \\
0 & 2 \\
5 & -2
\end{matrix}\right|
\\
\ \\
\left (\overrightarrow{u},\overrightarrow{v}, \overrightarrow{P_1P_0} \right ) = -2+20-2 = 16
$$
Em seguida, calculamos o produto vetorial:
$$
\overrightarrow{u} \times \overrightarrow{v} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
1 & 0 & -2\\
0 & 2 & -1
\end{vmatrix}
\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
1 & 0 & -2\\
0 & 2 & -1
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
1 & 0\\
0 & 2
\end{matrix}\right|
\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} = 2\vec{k}+4\vec{i}+\vec{j}\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} = (4,1,2)
$$
d(r,s) = \frac{\left \| 16 \right \|}{\left \| (4,1,2) \right \|}\\
\ \\
d(r,s) = \frac{\sqrt{16}}{\sqrt{16+1+4}}\\
\ \\
d(r,s) = \frac{4}{\sqrt{21}}\ u.c.
$$
\pi: \ ax+by + cz + d = 0 \tag{4.1}
$$
d(P_0,\pi) = \left \| \overrightarrow{AP_0} \right \|
$$
\overrightarrow{u} \times \overrightarrow{v} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
1 & 0 & -2\\
0 & 2 & -1
\end{vmatrix}
\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} =
\begin{vmatrix}
\vec{i} & \vec{j} & \vec{k}\\
1 & 0 & -2\\
0 & 2 & -1
\end{vmatrix}
\left.\begin{matrix}
\vec{i} & \vec{j}\\
1 & 0\\
0 & 2
\end{matrix}\right|
\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} = 2\vec{k}+4\vec{i}+\vec{j}\\
\ \\
\overrightarrow{u} \times \overrightarrow{v} = (4,1,2)
$$
Aplicamos na fórmula obtida em $(3.3.3)$:
$$d(r,s) = \frac{\left \| 16 \right \|}{\left \| (4,1,2) \right \|}\\
\ \\
d(r,s) = \frac{\sqrt{16}}{\sqrt{16+1+4}}\\
\ \\
d(r,s) = \frac{4}{\sqrt{21}}\ u.c.
$$
Assim, a ditância entre as retas $r$ e $s$ mede $\displaystyle \frac{4}{\sqrt{21}}$ unidades de comprimento.
4) Distância de um ponto e um plano
Sejam um ponto $P_0(x_0, y_0, z_0)$ e um plano $\pi$ no espaço:
$$\pi: \ ax+by + cz + d = 0 \tag{4.1}
$$
Seja o ponto $A$ o pé da perpendicular conduzida pelo ponto $P_0$ sobre o plano $\pi$ e seja $P_(x,y,z)$ um ponto qualquer pertencente a $\pi$.
[imagem 4]
Se um vetor $\overrightarrow{n}=(a,b,c)$ é normal ao plano $\pi$, então o vetor $\overrightarrow{AP_0}$ tem a mesma direção de $\overrightarrow{n}$.
A distância $d$ do ponto $P_0$ ao plano $\pi$ é dada por:
$$d(P_0,\pi) = \left \| \overrightarrow{AP_0} \right \|
$$
O vetor $\overrightarrow{AP_0}$ é a projeção ortogonal do vetor $\overrightarrow{PP_0}$ sobre $\pi$ na direção de $\overrightarrow{n}$.
Utilizar a fórmula para projeção evita ter que calcular $A$. A fórmula utilizada para o vetor projeção de um vetor $\overrightarrow{u}$ sobre um vetor $\overrightarrow{v}$ é dada por:
$$\text{Proj}_{\displaystyle \overrightarrow{v}}\overrightarrow{u} = \left ( \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\overrightarrow{v}\cdot \overrightarrow{v}} \right )\cdot \overrightarrow{v}
$$
Aplicando ao nosso problema, temos que:
$$
d(P_0,\pi) = \left | AP_0 \right | \\
\ \\
d(P_0,\pi) = \left \| \frac{\overrightarrow{PP_0}\cdot \overrightarrow{n}}{\left \| \overrightarrow{n} \right \|^2} \cdot \overrightarrow{n} \right \|\\
\ \\
d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |\ \left \| \overrightarrow{n} \right \| }{\left \| \overrightarrow{n} \right \|^2}\\
$$
d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |}{\left \| \overrightarrow{n} \right \|} \tag{4.2}
$$
d(P_0,\pi) = \left | AP_0 \right | \\
\ \\
d(P_0,\pi) = \left \| \frac{\overrightarrow{PP_0}\cdot \overrightarrow{n}}{\left \| \overrightarrow{n} \right \|^2} \cdot \overrightarrow{n} \right \|\\
\ \\
d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |\ \left \| \overrightarrow{n} \right \| }{\left \| \overrightarrow{n} \right \|^2}\\
$$
O que nos leva a:
$$d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |}{\left \| \overrightarrow{n} \right \|} \tag{4.2}
$$
No entanto, temos que:
$$\overrightarrow{PP_0} = (x_0-x, y_0-y, z_0-z) \tag{4.3}
$$
E que:
$$\overrightarrow{n} = (a,b,c) \tag{4.4}
$$
E ainda:
$$\left \| \overrightarrow{n} \right \| = \sqrt{a^2+b^2+c^2} \tag{4.5}
$$
Substituindo $(4.3)$, $(4.4)$ e $(4.5)$ em $(4.2)$
$$
d(P_0,\pi) = \frac{\left | (x_0-x,y_0-y, z_0-z) \cdot (a,b,c) \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\
d(P_0,\pi) = \frac{\left | a(x_0-x), b(y_0-y), c(z_0-z) \right |}{\sqrt{a^2+b^2+c^2}}
$$
d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0-ax-by-cz \right |}{\sqrt{a^2+b^2+c^2}} \tag{4.6}
$$
d(P_0,\pi) = \frac{\left | (x_0-x,y_0-y, z_0-z) \cdot (a,b,c) \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\
d(P_0,\pi) = \frac{\left | a(x_0-x), b(y_0-y), c(z_0-z) \right |}{\sqrt{a^2+b^2+c^2}}
$$
Encontramos:
$$d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0-ax-by-cz \right |}{\sqrt{a^2+b^2+c^2}} \tag{4.6}
$$
Mas, da equação de $pi$, dada em $(4.1)$, temos:
$$
ax+by+cz+d=0
$$Isolando $d$, obtemos:
$$ax+by+cz+d=0
$$Isolando $d$, obtemos:
d = -ax-by-cz \tag{4.7}
$$
Substituindo $(4.7)$ em $(4.6)$:
$$d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\sqrt{a^2+b^2+c^2}} \tag{4.8}
$$
O numerador da fórmula acima é o módulo do número que se obtém substituino $x$, $y$ e $z$ no primeiro membro da equação geral do plano $\pi$ pelas coordenadas do ponto $P_0$ e o denominador é o módulo do vetor normal ao plano. Assim:
$$d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\left \| \overrightarrow{n} \right \|} \tag{4.9}
$$
Se o ponto $P_0$ for a origem do sistema $O(0,0,0)$, então:
$$d(P_0,\pi) = \frac{\left | d \right |}{\left \| \overrightarrow{n} \right \|} \tag{4.10}
$$
Exemplo 6:
Vamos calcular a distância entre o ponto $P_0(-4,2,5)$ ao plano $\pi:\ 2x+y+2z+8=0$.
Temos que as coordenadas do ponto $P_0$ são dadas por:
$$\left\{\begin{matrix}
x_0 & = & -4\\
y_0 & = & 2 \\
z_0 & = & 5
\end{matrix}\right.
$$
E as coordenadas do vetor $\overrightarrow{n}$ são:
$$
\left\{\begin{matrix}
a & = & 2\\
b & = & 1 \\
c & = & 2
\end{matrix}\right.
$$Aplicando esses valores na fórmula para a distância de um ponto a um plano dada em $(4.8)$, obtemos:
$$\left\{\begin{matrix}
a & = & 2\\
b & = & 1 \\
c & = & 2
\end{matrix}\right.
$$Aplicando esses valores na fórmula para a distância de um ponto a um plano dada em $(4.8)$, obtemos:
d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\
d(P_0,\pi) = \frac{\left | 2(-4)+1(2)+2(5)+8 \right |}{\sqrt{2^2+1^2+2^2}}\\
\ \\
d(P_0,\pi) = \frac{\left | -8+2+10+8 \right |}{9}\\
\ \\
d(P_0,\pi) = \frac{12}{3} = 4\ u.c.
$$
Assim, a distância entre o ponto $P_0$ e o plano $\pi$ mede 4 unidades de comprimento.
5) Distância entre dois planos
A distância entre dois planos é definido apenas quando os planos forem paralelos.
Dados dois planos $\pi_1$ e $\pi_2$ paralelos, a distância $d$ entre eles é a distância de um ponto qualquer de um dos planos ao outro:
- $d(\pi_1,\pi_2) = d(P_0, \pi_2)$, com $P_0 \in \pi_1$
- $d(\pi_1,\pi_2) = d(P_0, \pi_1)$, com $P_0 \in \pi_2$
Exemplo 7:
Vamos calcular a distância entre os planos:
$$
\begin{cases}
\pi_1:\ 2x-2y+z-5=0\\
\pi_2:\ 4x-4y+2z+14=0
\end{cases}
$$Um ponto de $\pi_1$ é $P_0(0,0,5)$ e um vetor normal a $\pi_2$ é $\overrightarrow{n}=(4,4,-2)$
\begin{cases}
\pi_1:\ 2x-2y+z-5=0\\
\pi_2:\ 4x-4y+2z+14=0
\end{cases}
$$Um ponto de $\pi_1$ é $P_0(0,0,5)$ e um vetor normal a $\pi_2$ é $\overrightarrow{n}=(4,4,-2)$
Podemos utilizar os resultados anteriormente obtido em $(4.8)$:
$$d(\pi_1,\pi_2) = d(P_0,\pi_2) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\
d(P_0,\pi_2) = \frac{\left | 4(0)-4(0)+2(5)+14 \right |}{\sqrt{4^2+(-4)^2+2^2}} \\
\ \\
d(P_0,\pi_2) = \frac{\left | 10+14 \right |}{\sqrt{36}}\\
\ \\
d(P_0,\pi_2) = \frac{24}{6} = 4\ u.c.
$$
Outra forma de resolver este problema e ver que, como os planos são paralelos, são da forma:
\begin{cases}\pi_1:\ a_1x+b_ay+c_1z+d_1=0\\
\pi_2:\ a_2x+b_2y+c_2z+d_2=0
\end{cases}
E como são paralelos, podemos obter:
$$\left\{\begin{matrix}
a_1 & = & a_2 & = & a \\
b_1 & = & b_2 & = & b \\
c_1 & = & c_2 & = & c
\end{matrix}\right.
$$
Levando em consideração a fórmula $(4.8)$:
$$d(\pi_1,\pi_2) = d(P_0,\pi_1) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\sqrt{a^2+b^2+c^2}}
$$
e que podemos reescrever a equação de $\pi_2$ como:
$$ax_0+by_0+cz_0=-d_2
$$
obtemos:
$$d(\pi_1,\pi_2) = \frac{\left | d_1-d_2 \right |}{\sqrt{a^2+b^2+c^2}}
$$
Se multiplicarmos a equação de $\pi_2$ por $1/2$ e aplicarmos na equação anterior:
$$d(\pi_1,\pi_2) = \frac{\left | d_1-d_2 \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\
d(\pi_1,\pi_2) = \frac{\left | -5-7 \right |}{\sqrt{2^2+(-2)^2+1^2}}\\
\ \\
d(\pi_1,\pi_2) = \frac{12}{3}=4\ u.c.
$$
6) Distância entre uma reta e um plano
A distância de uma reta a um plano é definida apenas quando a reta é paralela ao plano.
Seja uma reta $r$ paralela a um plano $\pi$. A distância $d$ da reta ao plano é a distância de um ponto qualquer da reta ao plano:
Exemplo 8:
Vamos calcular a distância entre a reta $r$ paralela ao plano $\pi$ definido por:
$$\left\{\begin{matrix}
r:\ x-2=y=z+1\\
\pi:\ x+y-2z+3=0
\end{matrix}\right.
$$
Um ponto $P_0$ pertencente à reta $r$ é o ponto $P_0(2,0,-1)$.
Utilizando a fórmula $(4.8)$:
$$d(P_0,\pi) = \frac{\left | 1(2)+1(0)-2(-1)+3 \right |}{\sqrt{1^2+1^2+(-2)^2}}\\
\ \\
d(P_0,\pi) = \frac{\left | 2+2+3 \right |}{\sqrt{6}}\\
\ \\
d(P_0,\pi) = \frac{7}{\sqrt{6}}\ u.c.
$$
Assim, a distância entre a reta $r$ e o plano $\pi$ mede $7/ \sqrt{6}$ unidades de comprimento.
Referências:
- Geometria Analítica - Steinbruch & Winterle
- Geometria Analítica - Boulos & Camargo





Olá, meu amigo! Que trabalhão editar todo esse artigo! Sensacional!
ResponderExcluirDepois de Álgebra Linear, Geometria Analítica era a minha grande paixão na época da faculdade. Os grupos de estudos tinham aluno de Matemática, Física, Química, etc. Era uma diversão!
Observar esse post me trouxe ótimas recordações, e é claro vai ser útil para muitas pessoas.
Um abraço!
Olá Edigley! Deu um trabalho mesmo, mas eu gosto, é prazeroso ver o resultado.
ExcluirEu gostava bastante de geometria analítica e algebra linear, mas o que mais me fascinava era história da matemática.
Espero que seja útil para os leitores.
Um abraço!
Ah, História da Matemática é muito bom também.
ResponderExcluir