Como obter a equação reduzida da reta

Este artigo é sobre como obter a equação reduzida da reta utilizando-se do fato que uma reta passa por dois pontos distintos em um plano e que toda reta não-vertical possui uma inclinação.

Veremos a construção da demonstração da equação reduzida da reta passo-a-passo e outros tópicos importantes sobre o estudo da reta.

Conteúdo:
1. A equação reduzida da reta
2. Exemplo
2.1. O coeficiente angular
2.2. O coeficiente linear
2.3. A equação reduzida da reta
2.4. A raiz da equação da reta
2.5. Tabela de valores
3. Comportamento de uma reta
3.1. Coeficiente angular (m)
3.2. Coeficiente linear (b)
3.3. Variável independente (x)
3.4. Variável dependente (y)
4. Estudo da equação da reta com GeoGebra

1. A equação reduzida da reta

A inclinação de uma reta também é chamada de coeficiente angular da reta e recebe esse nome porque o "coeficiente" está multiplicando a variável independente $x$ e o termo "angular" está associado ao ângulo formado pela reta e o eixo das abscissas.

O coeficiente angular de uma reta que passa pelos pontos $A$ e $B$ é dado pela tangente do ângulo formado, pois é definido pela razão entre a elevação e a distância.

Assim, a inclinação é dada por:

$$
\text{tg}(\theta) = \frac{\text{elevação}}{\text{distância}}\\
\ \\
\text{tg}(\theta) = \frac{\text{cateto oposto}}{\text{cateto adjacente}}\\
\ \\
\text{tg}(\theta) = \frac{y_2-y_1}{x_2-x_1}
$$

Quando estudamos a reta é mais comum representarmos o coeficiente angular com a letra $m$. Assim:

$$
m = \frac{y_2-y_1}{x_2-x_1}
$$

Se a reta $r$ for paralela ao eixo dos $x$, então sua inclinação será zero, uma vez que $y_2=y_1$ e seu coeficiente angular será igual a $0$.

$$
m = \frac{y_2-y_1}{x_2-x_1}=\frac{0}{x_2-x_1}=0
$$

Mas, se $r$ for paralela ao eixo dos $y$, a reta $r$ não possui um coeficiente angular definido, uma vez que $x_2=x_1$.

$$
m = \frac{y_2-y_1}{x_2-x_1}=\frac{y_2-y_1}{0}=\infty
$$

Deste modo, podemos dizer que em uma reta vertical, cujo ângulo formado com o eixo dos $x$ mede $90°$, não existe um coeficiente angular.

Sendo assim, qualquer reta não-vertical possui um coeficiente angular e, consequentemente, cortará o eixo dos $y$ em algum ponto (na verdade, em ambos os eixos).

Se chamarmos de $b$ o ponto onde a reta intercepta o eixo dos $y$, obrigatoriamente teremos que $x=0$. Esse ponto é chamado de coeficiente linear e também é o termo independente da equação da reta, ou seja, o termo que não acompanha a variável $x$.

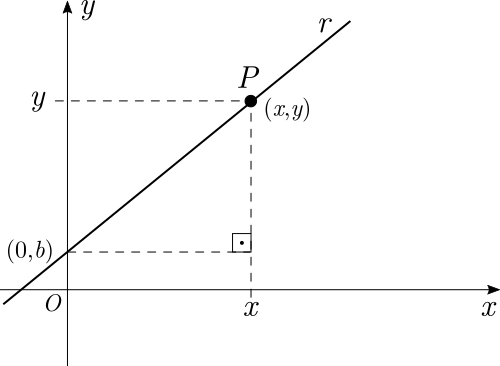
Seja $P$ um ponto qualquer sobre a reta $r$ de coordenadas $(x,y)$:

Se utilizarmos a fórmula para o coeficiente angular da reta, aplicando no gráfico acima, e como resultado obteremos:

$$
m=\frac{y_2-y_1}{x_2-x_1}\\
\ \\
m=\frac{y-b}{x-0}\\
\ \\
m = \frac{y-b}{x}\\
\ \\
mx = y-b\\
\ \\
y = mx + b
$$

Essa é a equação reduzida da reta, que passa por um ponto $P(x,y)$, possui um coeficiente angular $m$ e coeficiente linear $b$.

Em inglês, esta equação reduzida da reta é chamada de fórmula slope-intercept, ou seja, fórmula inclinação-intercepto, porque utiliza-se da inclinação $m$ e o intercepto em $y$ (ponto onde a reta intercepta o eixo dos $y$).

2. Exemplo

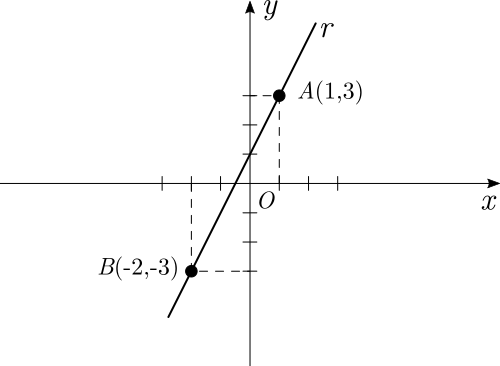
Seja uma reta $r$ definida pelos pontos $A(1,3)$ e $B(-2,-3)$. Vamos a partir deste exemplo encontrar o coeficiente angular, o coeficiente linear, a equação reduzida da reta, a raiz da equação e criar uma tabela de valores.

2.1. O coeficiente angular $(m)$

O coeficiente angular é dado pela fórmula da inclinação:

$$
m = \frac{y_2-y_1}{x_2-x_1}\\
\ \\
m = \frac{-3-3}{-2-1}\\
\ \\
m = \frac{-6}{-3}\\
\ \\
m = 2
$$

Assim, a reta possui um coeficiente angular $m=2$.

2.2. Coeficiente linear $(b)$

Para determinarmos o ponto $P$ em que a reta intercepta o eixo dos $y$, basta fazermos a coordenada $x$ do ponto $P$ igual a zero.

Tomamos como referência o ponto $A(1,3)$ (mas poderia ser o ponto $B$ sem qualquer problema) e o ponto $P(0,y)$:

$$
m = \frac{y_2-y_1}{x_2-x_1}\\
\ \\
2 = \frac{y-3}{0-1}\\
\ \\
2 = \frac{y-3}{-1}\\
\ \\
-2 = y-3\\
\ \\
y = 1
$$

Portanto, o coeficiente linear da reta $r$ é igual a $b=1$.

2.3. Equação reduzida da reta $(y=mx+b)$

Para encontrarmos a equação reduzida da reta que passa pelos pontos $A(1,3)$ e $B(-2,-3)$ utilizamos a fórmula da inclinação e o valor do coeficiente angular $m=2$:

$$
m = \frac{y_2-y_1}{x_2-x_1}
$$

Vamos tomar o ponto $A(1,3)$ como referência (mas poderia ser o ponto $B$ sem problemas). Assim, fazemos $x_2=1$ e $y_2=3$ e tomamos um ponto genérico de coordenadas $(x,y)$. Assim:

$$
m = \frac{y_2-y_1}{x_2-x_1}\\
\ \\
2 = \frac{3-y}{1-x}\\
\ \\
2 (1-x) = 3-y\\
\ \\
2-2x=3-y\\
\ \\
y = 2x-2+3\\
\ \\
y = 2x+1
$$

E como resultado, $y=2x+1$ é a equação reduzida da reta que passa pelos pontos $A(1,3)$ e possui inclinação $m=2$.

2.4. Raiz da equação da reta

Para determinarmos o ponto em que a reta corta o eixo dos $x$, basta adotarmos a coordenada $y=0$.

Vamos tomar o ponto $A(1,3)$ como referência. Seja $R(x,0)$ o ponto em que a reta corta o eixo dos $x$. Temos que:

$$
m = \frac{y_2-y_1}{x_2-x_1}\\
\ \\
2 = \frac{0-3}{x-1}\\
\ \\
2(x-1) = -3\\
\ \\
2x-2 = -3\\
\ \\
2x = -1\\
\ \\
x= -\frac{1}{2}
$$

O ponto em que a reta corta o eixos dos $x$ também é chamado de raiz da equação e pode ser obtido através da equação da reta $y=2x+1$, fazendo a coordenada $y=0$:

$$
2x+1=0
$$

E para determinar a raiz da equação, basta encontrarmos o valor de $x$ isolando-o:

$$
2x+1=0\\
\ \\
2x=-1\\
\ \\
x=-\frac{1}{2}
$$

Vejam que é o mesmo valor obtido através da fórmula do coeficiente angular, quando substituímos a coordenada $y$ por zero. O resultado não surpreende, mas conforta.

2.5. Tabela de valores

Através da equação da reta, podemos determinar quaisquer outros pontos da reta, basta simplesmente substituirmos a coordenada $x$ para obtermos o valor de $y$ correspondente.

\begin{array}{ | c | c |}
\hline
{\color{red}{x}} & \color{blue}{y}=2\color{red}{x}+1\\
\hline
\color{red}{3} & y=2(\color{red}{3})+1=\color{blue}{7}\\
\hline
\color{red}{2} & y=2(\color{red}{2})+1=\color{blue}{5}\\
\hline
\color{red}{1} & y=2(\color{red}{1})+1=\color{blue}{3}\\
\hline
\color{red}{0} & y=2(\color{red}{0})+1=\color{blue}{1}\\
\hline
\color{red}{-1} & y=2(\color{red}{-1})+1=\color{blue}{-1}\\
\hline
\color{red}{-2} & y=2(\color{red}{-2})+1=\color{blue}{-3}\\
\hline
\color{red}{-3} & y=2(\color{red}{-3})+1=\color{blue}{-5}\\
\hline
\end{array}

3. Comportamento de uma reta

Quando analisamos graficamente a reta, podemos perceber alguns comportamentos em que a curva obedece quando variamos seus parâmetros.

Vamos tomar como exemplo uma reta genérica, cuja equação reduzida seja $y=mx+b$.

3.1. Coeficiente angular $(m)$

O coeficiente angular $m$, como já vimos, está relacionado com a inclinação da reta. Quando a reta é paralela ao eixo dos $x$ seu coeficiente angular vale zero e quando a reta é perpendicular ao eixo dos $x$, seu coeficiente angular não existe.

Através do sinal do coeficiente angular conseguimos saber se a reta é crescente ou decrescente.

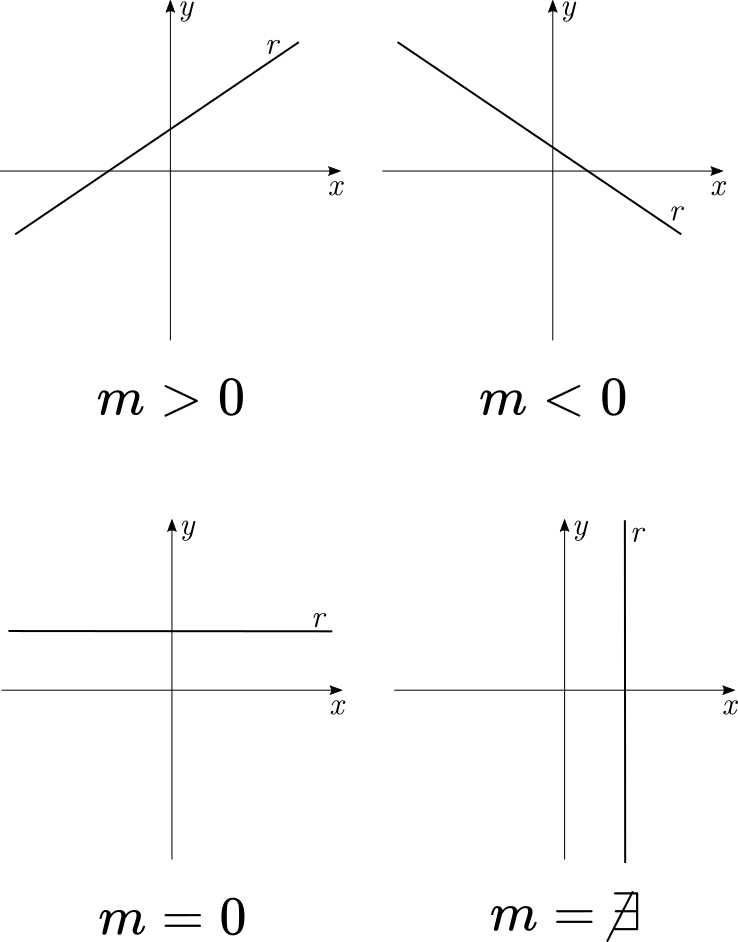
$m>0$: A reta é crescente
$m<0$: A reta é decrescente

o-sinal-do-coeficiente-angular-determina-se-a-reta-e-crescente-ou-decrescente

Assim:

Quanto maior o valor absoluto de $m$, maior a inclinação da reta e cada vez mais ela se aproxima de uma reta vertical.
Quanto mais próximo de zero o valor de $m$ se encontra, menor é seu coeficiente angular e a reta se aproxima a uma reta paralela ao eixo dos $x$.

3.2. Coeficiente linear $(b)$

O coeficiente linear $b$ é o termo independente da equação, ou seja, é aquele que não acompanha a variável $x$ e representa o ponto em que a reta cruza com o eixo dos $y$.

Através do sinal de $b$ conseguimos saber se a reta intercepta o eixo dos $y$ em seu semi-eixo positivo ou negativo:

$b>0$: A reta intercepta o eixo $y$ em seu semi-eixo positivo (acima do eixo dos $x$.
$b<0$: A reta intercepta o eixo dos $y$ em seu semi-eixo negativo (abaixo do eixo dos $x$.

3.3. Variável independente $(x)$

A variável independente é a variável $x$, correspondente ao eixo das abscissas, e representa uma grandeza que está sendo manipulada.

A cada valor específico atribuído a $x$, obtemos um resultado diferente, expresso em $y$. Um exemplo é a construção de um gráfico, mediante a uma equação ou função dada. Para cada valor atribuído a $x$, obtemos um valor de $y$ específico, que é o resultado e é chamado de variável dependente.

3.4. Variável dependente $(y)$

A variável dependente da equação reduzida da reta é a variável $y$, associada ao eixo das ordenadas. Recebe esse nome porque depende de como a variável independente se comporta, ou seja, para cada valor atribuído a $x$, obtemos um valor de $y$ específico, que é o resultado e é chamado de variável dependente.

4. Estudo da equação da reta com o GeoGebra

GeoGebra é um aplicativo de matemática dinâmica que combina conceitos de geometria e álgebra em uma única GUI. Sua distribuição é livre, nos termos da GNU General Public License, e é escrito em linguagem Java, o que lhe permite estar disponível em várias plataformas.

O Professor Edigley Alexandre criou um material no GeoGebra com um estudo sobre a reta através da equação reduzida da reta.

Você pode clicar nos botões abaixo para acessar o material direto em seu navegador ou pode fazer o download do arquivo.

Estudo da reta no GeoGebra Downoad do material GeoGebra

E você pode também ler um outro artigo sobre O uso do GeoGebra em aulas no estudo da equação da reta no blog do Professor Edigley.

01/01/2022