Regressão Linear é o processo estatístico que procura determinar a equação matemática mais adequada para definir a relação entre duas variáveis.
Muitas vezes a posição dos pontos experimentais no diagrama de dispersão sugere a existência de uma relação funcional entre as duas variáveis.
Assim, se os pontos experimentais se apresentarem como na figura 1, podemos admitir um relacionamento funcional entre as variáveis x e y, que são responsáveis pelo aspecto do diagrama, explicando grande parte das variações de x e y. Este relacionamento funcional corresponderia à linha existente na figura, que seria a linha de regressão.

Uma parcela da variação, entretanto, permanece, em geral, sem ser explicada e será atribuída ao acaso. Em outras palavras, admitimos existir uma função que justifica, em média, a variação das variáveis com a outra.
Na prática, os pontos experimentais terão uma variação em torno da linha representativa dessa função, devido à existência de uma variação aleatória adicional, chamada de variação residual.
Essa função de regressão, portanto, nos dá o valor médio de uma das variáveis em função da outra. Por exemplo, µ(y / x). Desta forma examinado será, dado os pontos experimentais, o de realizar uma indução quanto à expressão matemática da função de regressão.
Suponhamos que a linha de regressão seja uma reta e desejamos estabelecer a regressão y em função de x. A função desejada será da forma:
Os parâmetros α e β da reta teórica podem ser estimado através dos pontos experimentais fornecido por uma amostra, obtendo uma reta estimativa da forma:
Onde a é a estimativa do parâmetro α e b também chamado de coeficiente de regressão linear, é a estimativa do parâmetro β. O símbolo ŷ é utilizado para uma distinção dos valores dados pela reta estimativa, das ordenadas dos pontos experimentalmente obtidos.
A aplicação do princípio de ajustamento linear leva ao procedimento de mínimos quadrados, segundo o qual a reta a ser adotada deverá ser aquela que torna mínima a soma dos quadrados das distâncias da reta aos pontos experimentais, medidas no sentido da variação aleatória, que, como estamos considerando somente a variável y como aleatória, essas distâncias serão medidas na direção vertical.
Devemos procurar a reta para a qual se consiga minimizar:
sendo as distâncias di , como as indicadas na figura 2:

Na equação (1), devemos impor a condição:
Os valores a e b que minimizam essa expressão serão aqueles que anulam as derivadas parciais dessa expressão:
Da última forma da equação (2), fazemos as derivadas parciais (3):
As equações (4) e (5) nos fornecem um sistema linear de duas equações e duas incógnitas:
De (4) temos:
Onde n é o número de dados experimentais.
De (5) temos:
Associando (6) e (7) obtemos o sistema linear:
Os pontos experimentais fornecem os elementos para a montagem desse sistema, cuja solução fornecerá os coeficientes a e b.
Exemplo: Vamos obter a equação da reta de mínimos quadrados, tomando os dados experimentais da tabela abaixo:
Temos os valores experimentais de x e y. No sistema linear dado em (8), há algumas combinações que ainda devemos calcular: n, xi yi, xi2. Vamos montar uma tabela para melhor organizar os dados:
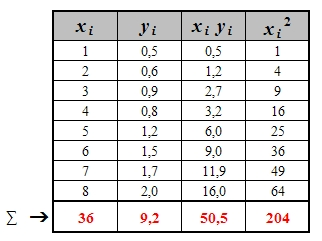
Temos várias formas de resolução de um sistema linear. Um método alternativo é o Método de Castilhos (veja aqui).
Resolvendo o sistema, encontramos:
Substituímos os valores encontrados para a e b na equação (1):
Que é a equação da reta de mínimos quadrados.
Podemos esboçar um gráfico de dispersão associado à reta de regressão:
[Figura 3: Reta de regressão]
Veja mais:
Regressão Polinomial
Polinômio Interpolador de Lagrange
Interpolação Polinomial no Blog Fatos Matemáticos: Parte 1, Parte 2 e Parte 3


![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhyPxR6Sg_L3a7Ugrc151ptDUw-pikNLHnZYoWzWabsUCm6s0W0WbKmzjy5elFljJTLY_oX3ioDz-8qGH9bJmHCSTDHjL-mrPdQuzEIHL-KfFCaaPlOF2yH_jkcL77XKU7_gzu9SaKnBamh/?imgmax=800)
![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgvwaC91pSC8vToFk597GxnVwG8XI_hToLOr36HgbaqUzTmVxRltDU8tfJ92kPAWXCxdNm65MuhQHveXBQ9__okMT0ST-9pqb1X0UD5MdGGZcfXAknkLSnSr_DoabYz3SJgNy1yvKiHYPo9/?imgmax=800)
![clip_image006[4] clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjxIdkUqQOHZWUzD_p5VcnZsUaQuOeH9rfRaiEBkL0CvslUFqmBqnd6ZQ2tNjMGGSl9hUN15QtJoUJphWXWtfv3_ankCvHI9FN9y9BAZ8mwMQWVT3DfDL_nnbEqN7AS74A-9yS1ZR0RN8yb/?imgmax=800)
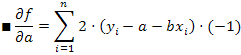













Obrigado por citar o meu blog. Mas novamente, venho parabenizá-lo pela sua didática e exposição de um assunto tão interessante como esta.
ResponderExcluirAbraços!
Cara, que demonstração chapada! Na facu só aprendemos fórmulas prontas. Agora ficou tudo esclarecido! Abçs
ResponderExcluirAmigo, nunca vi um blog tão interessante quanto este!!! Meus e de todos os acadêmicos do Brasil, PARABÉNS!
ResponderExcluirAgora se não é pedir muito, poderia postar um exemplo de regressão linear onde pontos experimentais possuem incertezas de medição??
Desde já grato!!!
Olá Alisson, agradeço seu gentil comentário.
ResponderExcluirVeja este pdf, onde tem um estudo sobre cálculo das incertezas. Veja página 45 em diante:
http://www.peb.ufrj.br/cursos/COB783/ErrosIncertezas.pdf
É um estudo bem interessante.
Para sabermos se usamos uma regressão linear ou quadrática, temos que obervar a dispersão dos pontos amostrais e definir que tipo de regressão melhor se aplica. Vou procurar um exemplo nas minhas notas de aula e depois publico aqui.
Um abraço.
Muito bom o método. Só gostaria de entender por que eu posso afirmar que os valores de a e b que minimizam a função são aqueles que anulam a derivada parcial dela. Obrgado
ResponderExcluir