Relações métricas no triângulo retângulo

O triângulo retângulo é aquele que possui um de seus ângulos igual a 90° e apresenta diversas relações interessantes. Neste artigo, veremos algumas relações métricas utilizando semelhança de triângulos.

As relações métricas são aquelas que envolvem as medidas dos lados do triângulo retângulo e alguns de seus segmentos.

Primeiramente vamos relembrar algumas definições que serão importantes nas demonstrações.

Definição 1: Triângulo retângulo

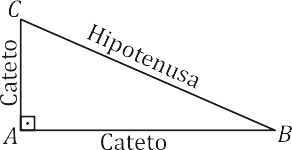
Um triângulo é chamado de triângulo retângulo se possuir um ângulo interno reto. O lado oposto ao ângulo reto recebe o nome de hipotenusa e os outros dois lados que formam o ângulo reto são chamados de catetos.

Definição 2: Semelhança de triângulos:

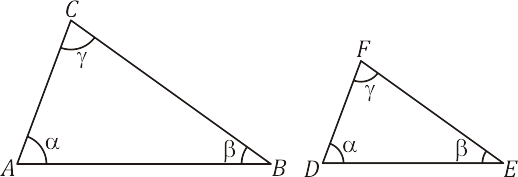
Dois triângulos são semelhantes se, e somente se, existe uma correspondência biunívuca, que associa os três vértices de um triângulo aos três vértices do outro triângulo, tais que:

• Ângulos com vértices correspondentes são congruentes;
• Lados opostos a vértices correspondentes são iguais.

\begin{equation*}
\triangle ABC \sim \triangle DEF \Longleftrightarrow \frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}
\end{equation*}
e
\begin{cases}
\hat{A} \cong \hat{D}\\
\ \\
\hat{B} \cong \hat{E}\\
\ \\
\hat{C} \cong \hat{F}
\end{cases}

Seja o triângulo $ABC$, reto em $\hat{A}$:

Temos que:

• $a$ é a hipotenusa;
• $b$ e $c$ são os catetos;
• $h$ é a altura do triângulo relativa à hipotenusa;
• $m$ é a projeção ortogonal do cateto $c$ sobre a hipotenusa;
• $n$ é a projeção ortogonal do cateto $b$ sobre a hipotenusa.

Demonstrações:

Para as demonstrações que seguem, vamos separar o triângulo $ABC$ em dois triângulos. Assim, teremos três triângulos semelhantes:

de modo que:
\begin{equation*}
\triangle ABC \sim \triangle DAB \sim \triangle DAC
\end{equation*}

1) O triângulo $ABC$ é semelhante ao triângulo $DBA$:
\begin{equation*}
\triangle ABC \sim \triangle DBA \Longleftrightarrow \frac{a}{c} = \frac{b}{h} = \frac{c}{m}
\end{equation*}
assim:
$$
ah = bc \tag{1}
$$
$$
c^2 = am \tag{2}
$$
$$
bm = ch \tag{3}
$$

2) O triângulo $ABC$ é semelhante ao triângulo $DAC$:
\begin{equation*}
\triangle ABC \sim \triangle DAC \Longleftrightarrow \frac{a}{b} = \frac{b}{n}= \frac{c}{h}
\end{equation*}
assim:
$$
ah = bc \tag{4}
$$
$$
b^2 = an \tag{5}
$$
$$
bh = cn \tag{6}
$$

3) O triângulo $DAB$ é semelhante ao triângulo $DAC$:
\begin{equation*}
\triangle DAB \sim \triangle DAC \Longleftrightarrow \frac{c}{b} = \frac{h}{n} = \frac{m}{h}
\end{equation*}
assim:
$$
cn = bh \tag{7}
$$
$$
bm = ch \tag{8}
$$
$$
h^2 = mn \tag{9}
$$

Somando membro a membro as relações $(2)$ e $(5)$, obtemos:

\begin{equation*}
b^2 + c^2 = an + am\\
\ \\
b^2 + c^2 = a(m + n)
\end{equation*}

No entanto, as projeções ortogonais $m$ e $n$ dos catetos $b$ e $c$ sobre a hipotenusa $a$, tem comprimento igual a $m+n=a$. Assim, chegamos ao Teorema de Pitágoras:

$$
b^2 + c^2 = a^2 \tag{10}
$$

Exemplo 1:

Determinar as medidas de $a$, $h$, $m$, e $n$ no triângulo $ABC$:

Da relação $(10)$, temos que:
$$
a^2 = b^2 + c^2\\
\ \\
a^2 = 3^2 + 4^2\\
\ \\
a^2 = 25\\
\ \\
a = 5
$$
Da relação $(4)$, temos que:
$$
ah = bc\\
\ \\
5h = 2 \cdot 4\\
\ \\
h = \frac{12}{5}
$$
Da relação $(2)$, temos que:
$$
c^2 = am \\
\ \\
3^2 = 5m\\
\ \\
m = \frac{9}{5}
$$
Da relação $(5)$, temos que:
$$
b^2 = an\\
\ \\
4^2 = 5n\\
\ \\
n = \frac{16}{5}
$$

Assim, os valores procurados são: $a=5$, $\displaystyle h=\frac{12}{5}$, $\displaystyle m=\frac{9}{5}$ e $\displaystyle n=\frac{16}{5}$.

Exemplo 2:

Calcular a altura relativa à base $\overline{BC}$ do triângulo isósceles abaixo:

Como o triângulo é isósceles, a altura $h$ divide o segmento $\overline{BC}$ em duas partes iguais. Assim, $\overline{BD} = \overline{CD}=4$. Aplicamos o teorema de Pitágoras no triângulo retângulo $DAC$:

$$
5^2 = 4^2 + h^2\\
\ \\
h^2 = 9\\
\ \\
h = 3
$$
A medida procurada é $h=3$.

Exemplo 3:

Num triângulo isósceles $ABC$, de lados iguais a $\overline{AB}=\overline{AC}=5$ e $\overline{BC}=8$, calcular a distância entre o ponto médio $M$ do segmento $\overline{BC}$ e um dos catetos.

Podemos representar o problema como a imagem abaixo:

Lembrando que a distância de um ponto a uma reta é o segmento que une o ponto à reta sendo perpendicular a ela. Na figura está representada pelo segmento $d = \overline{MN}$.

Primeiramente, vamos encontrar a medida h, utilizando-se do fato do triângulo ser isósceles. Assim, o segmento $\overline{CM}=4$. Aplicamos o teorema de Pitágoras:

$$
5^2 = 4^2 + h^2\\
\ \\
h^2 = 9\\
\ \\
h = 3
$$

Agora, podemos aplicar a relação $(1)$ no triângulo $ACM$ para encontrarmos o segmento $d$:

$$
5d = 3 \cdot 4\\
\ \\
5d = 12\\
\ \\
d = \frac{12}{5}
$$
Assim, a medida procurada é $d= 12 / 5$.

Referências:

• Matemática Volume Único - Manoel Paiva - Ed. Moderna

Links para este artigo:

• http://bit.ly/relacoes-metricas
• https://www.obaricentrodamente.com/2015/04/relacoes-metricas-no-triangulo-retangulo.html

Veja mais:

• Pontos notáveis de um triângulo
• Teorema da base média de um triângulo
• Demonstração da fórmula das coordenadas do baricentro do triângulo retângulo

Softwares utilizados:

• Inkscape