Como efetuar multiplicação por decomposição

Nosso sistema de numeração é chamado de indo-arábico e tem esse nome porque foi desenvolvido pelos antigos indianos que habitavam o vale do rio Indo e foi amplamente divulgado pelos árabes.

A multiplicação por decomposição é uma alternativa ao algoritmo usual e utiliza o princípio da decomposição dos números por unidades, dezenas, centenas, unidades de milhar, etc.

Fiquei motivado a escrever este artigo quando minha filha, que está no quarto ano, teve uma dúvida sobre este método. Depois que expliquei, ela conseguiu entender e resolveu os exercícios rapidamente Tentei escrever este artigo quase com as mesmas palavras. Espero que seja de fácil compreensão a você.

como-efetuar-multiplicacao-por-decomposicao-unidade-dezena-centena-milhar-o-baricentro-da-mente

O sistema indo-arábico é um sistema decimal, ou seja, os agrupamentos dos números são feitos de $10$ em $10$. É também um sistema posicional, ou seja, um determinado algarismo tem valores diferentes dependendo em que posição ele ocupa em um número.

Por exemplo, no número $19$, o número nove representa $9$ unidades e o número $1$ representa uma dezena (dez unidades). Mas, se trocarmos as posições entre estes algarismo, obteremos o número $91$, onde o número nove passa a valer $9$ dezenas (noventa unidades) e o número $1$, uma unidade.

Vamos iniciar recordando que os números são compostos por unidades $(u)$, dezenas $(d)$, centenas $(c)$, unidade de milhar $(um)$, dezenas de milhar $(dm)$, centenas de milhar $(cm)$, e assim por diante.

Por exemplo, vamos observar a composição do número $4.357$:

O número $4.357$ é composto por $7$ unidade, $5$ dezenas ($50$ unidades), $3$ centenas ($300$ unidades) e $4$ unidades de milhar ($4.000$ unidades). Se efetuarmos a soma dessas unidades, obteremos:

$$
7 + 50 + 300 + 4000 = 4357
$$

Multiplicação por decomposição:

Este método é bem simples e pode ser aplicado para a multiplicação de quaisquer números. No entanto, para números com muitos algarismos, fica inviável. Mas, se torna importante quando queremos explorar o conceito de composição dos números.

Se quisermos multiplicar dois números, primeiro decompomos estes números, e em seguida efetuamos a multiplicação entre cada parcela. O produto desejado será a soma de todas estas multiplicações.

Parece difícil? É mais simples do que parece. Vamos ver alguns exemplos para ficar claro.

Exemplo 1:

Vamos efetuar a multiplicação entre os números $123$ e $45$. Primeiro fazemos a decomposição de cada um deles:

O número $123$ é composto por $3$ unidades, $2$ dezenas e $1$ centena. Lembrando que $1$ centena é igual a $100$ unidades e $2$ dezenas é igual a $20$ unidades:

E o número $45$ é composto por $5$ unidades e $4$ dezenas. Lembrando que $4$ dezenas é igual a $40$ unidades:

Agora, montamos uma tabela escrevendo as decomposições dos números, sendo um na vertical e outro na horizontal:

O que fazemos agora é multiplicar os números e escrever o produto em cada célula. Fazemos as seguintes multiplicações:

$$
40 \times 100 = 4000\\
\ \\
40 \times 20 = 800\\
\ \\
40 \times 3 = 120\\
\ \\
5 \times 100 = 500\\
\ \\
5 \times 20 = 100\\
\ \\
5 \times 3 = 15
$$

Produtos entre as parcelas que compões os números 123 e 45

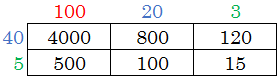
A princípio pode parecer trabalhoso porque efetuamos muitas multiplicações. Mas vejam que se torna simples, já que as multiplicações são simples. Por exemplo $40 \times 100$. apenas multiplicamos $4 \times 1=4$ e adicionamos $3$ algarismos $0$ (um que vem do $40$ e dois que vem do $100$).

O produto desejado é a soma de todas estas multiplicações:

\begin{equation*}
\begin{matrix}
& 4 & 0 & 0 & 0\\
& & 8 & 0 & 0\\
& & 1 & 2 & 0\\
& & 5 & 0 & 0\\
& & 1 & 0 & 0\\
+ & & & 1 & 5
\end{matrix}\\
\text{________________}\\
\begin{matrix}
& & 5 & 5 & 3 & 5
\end{matrix}
\end{equation*}

Lembrando que devemos escrever os números posicionando os números de modo que as todas as unidades, dezenas e centenas fiquem alinhados verticalmente.

Desta forma, $123 \times 45 = 5.535$.

Exemplo 2:

Vamos efetuar a multiplicação entre os números $4.872$ e $91$.

Analogamente ao que fizemos no exemplo anterior, vamos decompor cada um desses números e em seguida montar a tabela de multiplicação:

O número $4.872$ é composto por $2$ unidades, $7$ dezenas, $8$ centenas e $4$ unidades de milhar.

O número $91$ é composto por uma unidade e $9$ dezenas.

Assim, montamos a tabela:

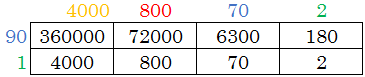
E o produto desejado será a soma de cada uma dessas multiplicações:
\begin{equation*}
\begin{matrix}
& 3 & 6 & 0 & 0 & 0 & 0\\
& & 7 & 2 & 0 & 0 & 0\\
& & & 6 & 3 & 0 & 0\\
& & & & 1 & 8 & 0\\
& & & 4 & 0 & 0 & 0\\
& & & & 8 & 0 & 0\\
& & & & & 7 & 0\\
+ & & & & & & 2
\end{matrix}\\
\text{_____________________}\\
\begin{matrix}
& & 4 & 4 & 3 & 3 & 5 & 2
\end{matrix}
\end{equation*}

Desta forma, $4872 \times 91 = 443.352$

Links para este artigo:

Veja mais:

Softwares utilizados:

Inkscape

14/08/2018