Como resolver multiplicação de matrizes de maneira simples

A multiplicação entre duas matrizes corresponde ao produto dessas matrizes. Para que seja possível efetuar essa multiplicação, é necessário que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz.

Uma matriz geralmente é representada por uma letra maiúscula e cada elemento por uma letra minúscula acompanhada pelos índices $ij$, onde $i$ representa a linha e $j$ representa a coluna dos elementos. Podemos escrever assim:

\begin{equation*}
A = \left(a_{ij}\right)_{m \times n}
\end{equation*}

O índice $m \times n$ indica que a matriz possui $m$ linhas e $n$ colunas.

Por exemplo, seja a matriz $A = \left( a_{ij}\right)_{2 \times 3}$:

\begin{equation*}
A =
\begin{bmatrix}
a_{11} & a_{12} & a_{13}\\
\ \\
a_{21} & a_{22} & a_{23}
\end{bmatrix}
\end{equation*}

A multiplicação entre duas matrizes é representada como $A \times B = C$, ou ainda:

\begin{equation*}
A_{m \times p} \times B_{p \times n} = C_{m \times n}
\end{equation*}
Os elementos da matriz $C_{m \times n}$ é dado por:
\begin{equation*}
c_{ik} = a_{i1} \cdot b_{1k} + a_{i2} \cdot b_{2k} + \cdots + a_{in} \cdot b_{nk}
\end{equation*}

Exemplo 1:

Vamos calcular o produto entre as matrizes abaixo:

\begin{equation*}
\begin{bmatrix}
\color{red}{1} & \color{green}{2} & \color{blue}{3}\\
4 & 5 & 6
\end{bmatrix}
\times
\begin{bmatrix}
\color{red}{7} & 8\\
\color{green}{9} & 10\\
\color{blue}{11} & 12\end{bmatrix}
=
\begin{bmatrix}
L_1C_1 & L_1C_2\\
L_2C_1 & L_2C_2
\end{bmatrix}
\end{equation*}

Onde $L$ representa uma linha e $C$ representa uma coluna. Cada elemento da matriz produto é dado por:

\begin{equation*}
L_1C_1 = \color{red}{a_{11}b_{11}} + \color{green}{a_{12}b_{21}} + \color{blue}{a_{13}b_{31}}\\
\ \\
L_1C_2 = a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}\\
\ \\
L_2C_1 = a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31}\\
\ \\
L_2C_2 = a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32}
\end{equation*}
Utilizando os elementos das matrizes, temos:
\begin{equation*}
L_1C_1 = \color{red}{1\cdot 7} + \color{green}{2\cdot 9} + \color{blue}{3\cdot 11} = 58\\
\ \\
L_1C_2 = 1\cdot 8 + 2\cdot 10 + 3\cdot 12 = 64\\
\ \\
L_2C_1 = 4\cdot 7 + 5\cdot 9 + 6\cdot 11 = 139\\
\ \\
L_2C_2 = 4\cdot 8 + 5\cdot 10 + 6\cdot 12 = 154
\end{equation*}
Então, o produto entre as matrizes é igual a:
\begin{equation*}
\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6
\end{bmatrix}
\times
\begin{bmatrix}
7 & 8\\
9 & 10\\
11 & 12
\end{bmatrix}
=
\begin{bmatrix}
58 & 64\\
139 & 154
\end{bmatrix}
\end{equation*}

Entendido como se efetua a multiplicação entre matrizes, vamos ver agora uma forma de representar a multiplicação de matrizes de uma maneira que seja fácil de memorizar e que não cause confusão na hora de efetuar as somas entre os produtos dos elementos das matrizes.

Exemplo 2:

Efetuar a multiplicação entre as matrizes $A$ e $B$, onde:

\begin{equation*}
A =
\begin{bmatrix}
1 & 0 & 3\\
-2 & 1 & 2
\end{bmatrix}
\qquad \text{e} \qquad
B =
\begin{bmatrix}
1 & 0\\
-1 & -2\\
0 & -3
\end{bmatrix}
\end{equation*}

Passo 1: Fazemos um retângulo, dividido em 4 partes e escrevemos as matrizes como na imagem abaixo:

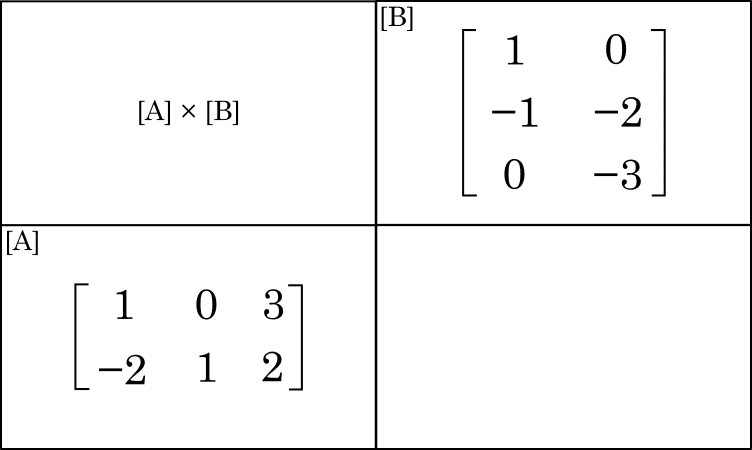
Passo 2: Multiplicamos os elementos da primeira linha da matriz $A$ pelos elementos da primeira coluna da matriz $B$. Fazemos:

\begin{equation*}
L_1C_1 = 1 \cdot 1 + 0 \cdot (-1) + 3\cdot 0 = 1
\end{equation*}

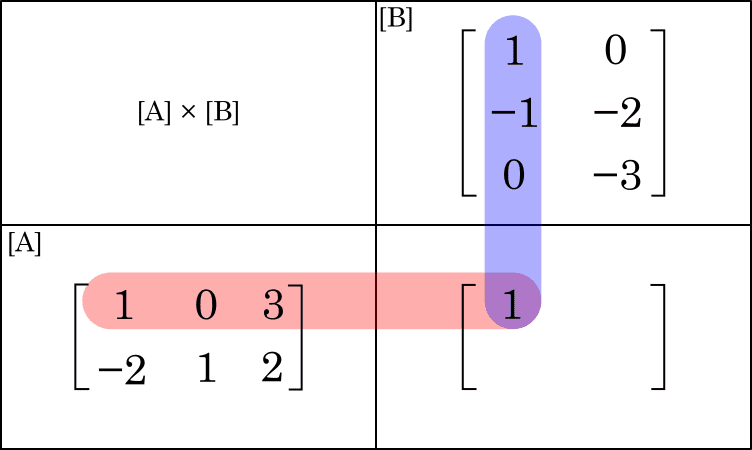
Passo 3: Multiplicamos os elementos da primeira linha da matriz $A$ pelos elementos da segunda coluna da matriz $B$. Fazemos:

\begin{equation*}
L_1C_2 = 1\cdot 0 + 0\cdot (-2) + 3\cdot (-3) = -9
\end{equation*}

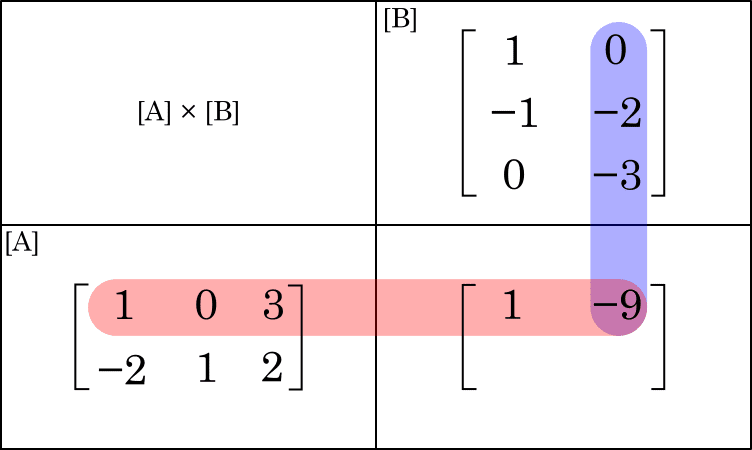
Passo 4: Multiplicamos os elementos da segunda linha da matriz $A$ pelos elementos da primeira coluna da matriz $B$. Fazemos:

\begin{equation*}
L_2C_1 = (-2) \cdot 1 + 1 \cdot (-1) + 2 \cdot 0 = -3
\end{equation*}

Passo 5: Multiplicamos os elementos da segunda coluna da matriz $A$ pelos elementos da segunda coluna da matriz $B$. Fazemos:

\begin{equation*}
L_2C_2 = (-2)\cdot 0 + 1 \cdot (-2) + 2 \cdot (-3) = -8
\end{equation*}

Então, a multiplicação entre as matrizes $A$ e $B$ é:

\begin{equation*}

\begin{bmatrix}
1 & 0 & 3\\
-2 & 1 & 2
\end{bmatrix}
\times
\begin{bmatrix}
1 & 0\\
-1 & -2\\
0 & -3
\end{bmatrix}
=
\begin{bmatrix}
1 & -9\\
-3 & -8
\end{bmatrix}
\end{equation*}

Acredito que dispor as matrizes dessa forma, fica mais intuitivo realizar a soma dos produtos dos elementos das matrizes $A$ e $B$.

Links para este artigo:

• http://bit.ly/multiplicacao-matrizes
• https://www.obaricentrodamente.com/2018/08/como-resolver-multiplicacao-de-matrizes-de-maneira-simles.html

Veja mais:

• Matrizes e o controle de tráfego
• Cayley e a teoria das matrizes
• Matrizes de rotação no R2
• Método de Castilho

Softwares utilizados:

• Inkscape