Tabela Price, também chamado de sistema francês de amortização, é um método usado em amortização de empréstimo cuja principal característica é apresentar prestações (ou parcelas) iguais. O método foi apresentado em 1771 por Richard Price em sua obra "Observações sobre Pagamentos Remissivos" (em inglês: Observations on Reversionary Payments).
O método foi idealizado pelo seu autor para pensões e aposentadorias. No entanto, foi a partir da 2ª revolução industrial que sua metodologia de cálculo foi aproveitada para cálculos de amortização de empréstimo. (Fonte: Wikpédia).
A planilha de amortização abaixo corresponde a um empréstimo de R$ 10.000,00, para ser pago em 5 prestações, à taxa de 10% ao mês.
Observando a planilha de amortização pelo SAF (Tabela Price), descobrimos que no plano de pagamento de empréstimo, as amortizações estão exatamente em progressão geométrica crescente com razão 1,1, ou seja:
$$\text{Razão}=\frac{1802}{1638}=\frac{1982}{1802}=\frac{2180}{1982}=\frac{2398}{2180}=1,1=1+0,10=1+i
$$
Teorema de Sebá:
No Sistema de Amortização Francês (SAF) a razão entre duas amortizações consecutivas quaisquer $A_1$ e $A_2$, onde $A_2>A_1$, é sempre igual à taxa do empréstimo ou do financiamento.
Demonstração:
Sejam:
- $R_k$ = valor da parcela de ordem $k$;
- $J_k$ = parcela de juros de ordem $k$;
- $A_k$ = parcela de amortização de ordem $k$.
Como o valor da prestação é composta pela parcela de amortização mais a parcela de juros, então:
$$R_k = A_k + J_k
$$
No período $k+1$, temos:
$$R_{k+1} = A_{k+1} + J_{k+1} \tag{1}
$$
Já que as prestações são constantes, logo:
$$R_k = R_{k+1} \tag{2}
$$
Substituindo $(2)$ em $(1)$, obtemos:
$$A_k + J_k = A_{k+1} + J_{k+1} \tag{3}
$$
Como a parcela de juros vai decrescendo, logo:
$$J_{k} - J_{k+1} > 0
$$
Já que a parcela de amortização vai crescendo, logo:
$$A_{k+1} - A_k > 0
$$
Sendo assim, a equação $(3)$ se transforma em:
$$A_{k+1} - A_k = J_k - J_{k+1}
$$
Como $A_{k+1} - A_k = J_k - J_{k+1} = i\ A_k$, onde $i$ é a taxa de juros, temos que:
$$A_{k+1} - A_k = i\ A_k\\
\ \\
A_{k+1} = A_k + i\ A_k\\
\ \\
A_{k+1} = A_k\ (1+i)\\
\ \\
\frac{A_{k+1}}{A_k} = 1+i
$$
Exemplo de aplicação:
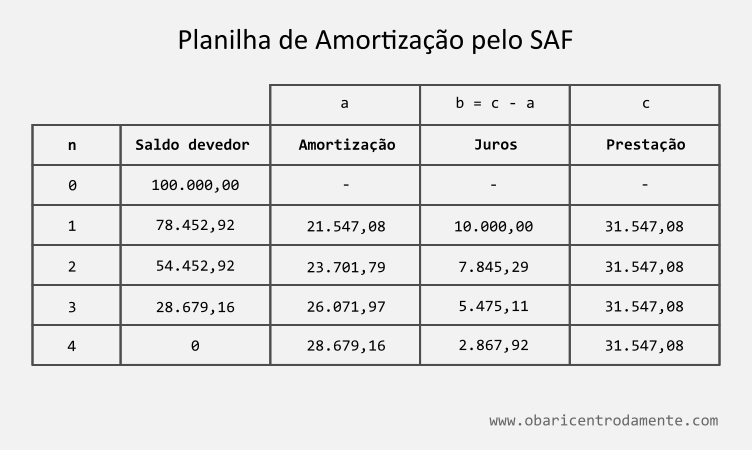
Suponha que você fez um financiamento de $R\$\ 100.000,00$ para ser pago pelo SAF em 4 prestações, cada uma no valor de $R\$\ 31.547,07$. Pergunta-se: qual a taxa mensal cobrada no financiamento?
Resolução:
Para você saber o valor da taxa cobrada no financiamento, basta escolher, na planilha de amortização fornecida pelo Banco, o valor de duas amortizações consecutivas e divida o maior valor pelo menor. Subtraia de 1 e multiplique o resultado por 100. Essa é a taxa de juros que o Banco está cobrando.
Suponha que você escolha, na coluna de amortizações, as duas primeiras amortizações:
- 1ª amortização: $A_1 = R\$\ 21.547,08$
- 2ª amortização: $A_2 = R\$\ 23.701,79$
Como $A_2>A_1$, logo, a taxa de juros $i$ cobrada pelo Banco é dada por:
$$i = \left( \frac{A_2}{A_1}-1\right) \cdot 100\\
\ \\
i = \left( \frac{23.701,79}{21.547,08}-1\right) \cdot 100\\
\ \\
i = 10\%
$$
que é a taxa de juros mensal.
Verificação:
Calculemos, com a taxa de 10% ao mês, o valor da prestação $R$:
$$R = \frac{P \cdot i}{1-(1+i)^{-n}}
$$
na qual:
- $R = R\$\ 31.547,07$ (Valor da prestação);
- $P = R\$\ 100.000,00$ (Valor atual ou valor financiado);
- $i = ?$ (Taxa de juros);
- $n = 4$ (Número de prestações).
R = \frac{P \cdot i}{1-(1+i)^{-n}}\\
\ \\
R = \frac{100.000 \cdot 0,10}{1-(1+0,10)^{-4}}\\
\ \\
R = R\$\ 31.547,07
$$
O valor calculado é igual ao que consta na última coluna da planilha de amortização.
Sobre o autor:
- Este artigo foi desenvolvido por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB.




Postar um comentário