Lembra daquelas tabelas de integrais? Quando estudamos em nossa graduação, muitas vezes somente consultamos as tabelas e tomamos o resultado. Mas como esses resultados foram obtidos?
Este artigo faz parte de uma série de resoluções de integrais que venho fazendo para demonstrar os resultados que encontramos nessas tabelas.
Primeiramente a integral é resolvida passo-a-passo e em seguida é aplicada em exemplos. Para cada integral, utiliza-se técnicas específicas para sua resolução, que pode ser por substituição, por partes, por frações parciais ou substituição trigonométrica ou ainda uma combinação de métodos.
Nesta postagem, vamos demonstrar que:
$$\int \frac{1}{\sqrt{ax+b}}\ dx = \frac{2\ \sqrt{ax+b}}{a}+C
$$
Seja a integral:
$$I = \int \frac{1}{\sqrt{ax+b}}\ dx
$$
sendo, $a$ e $b$ constantes, $a\neq 0$ e $ax+b>0$
Para o integrando, fazemos a substituição $u=ax+b$. Assim, $du=a\ dx$ e $\displaystyle dx=\frac{1}{a}du$:
$$I = \int \frac{1}{\sqrt{u}} \cdot \frac{1}{a}\ du\\
\ \\
I = \frac{1}{a} \int \frac{1}{\sqrt{u}}\ du\\
$$
A integral de $\displaystyle \frac{1}{\sqrt{u}}$ é $2\sqrt{u}$:
$$I = \frac{1}{a} \int \frac{1}{u^{1/2}}\ dx\\
\ \\
I = \frac{1}{a} \int u^{-1/2}\ dx\\
\ \\
I = \frac{1}{a} \cdot \frac{u^{-1/2+1}}{-1/2+1} + C\\
\ \\
I = \frac{1}{a} \cdot \frac{u^{1/2}}{1/2} + C\\
\ \\
I = \frac{2}{a} \cdot \sqrt{u} + C
$$
Mas, $u=ax+b$, assim:
$$I = \frac{2}{a} \cdot \sqrt{ax+b}+C
$$
Exemplo 1:
Vamos calcular a integral $\displaystyle \int \frac{1}{\sqrt{2x+1}}\ dx$:
Temos que:
$$I = \int \frac{1}{\sqrt{2x+1}}\ dx
$$
Neste caso, $a=2$ e $b=1$. Utilizando a fórmula encontrada anteriormente, fazemos:
$$I = \frac{2}{a} \sqrt{ax+b} + C\\
\ \\
I = \frac{2}{2} \sqrt{2x+1} + C\\
\ \\
I = \sqrt{2x+1} + C
$$
Exemplo 2:
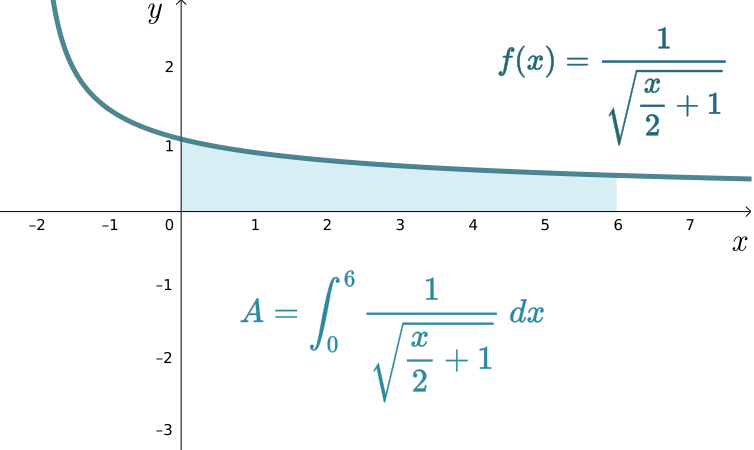
Vamos calcular a área sob a curva $\displaystyle f(x) = \frac{1}{\displaystyle \sqrt{\frac{x}{2}+1}}$ no intervalo de $x=0$ e $x=6$.
Para calcularmos a área desejada, utilizamos o conceito de integral definida, com limites de integração inferior e superior iguais a $0$ e $6$, respectivamente.
Utilizando o resultado obtido anteriormente, temos que $a=1/2$ e $b=1$. Assim:
$$A = \int_0^6 \frac{1}{\displaystyle \sqrt{\frac{x}{2}+1}}\ dx\\
\ \\
A = \left[ \frac{2}{\displaystyle \frac{1}{2}} \cdot \sqrt{\frac{x}{2}+1} \right]_0^6\\
\ \\
A = \left[ 4\cdot \sqrt{\frac{x}{2}+1}\ \right]_0^6\\
\ \\
A = 4\sqrt{\frac{6}{2}+1} - 4\sqrt{\frac{0}{2}+1}\\
\ \\
A = 4\sqrt{3+1} - 4\sqrt{1}\\
\ \\
A = 8 - 4\\
\ \\
A = 4\ u.a.
$$
Desta forma, a área desejada vale 4 unidades de área.



Postar um comentário