Na Geometria Plana, Pipa (também chamado de deltoide) é um quadrilátero com um eixo de simetria dividindo-o em dois pares disjuntos de lados adjacentes congruentes.
O nome "pipa" é uma referência ao brinquedo que leva o mesmo nome, içada por uma linha e soprada pelo vento.
Segundo o matemático alemão Olaus Henrici (1840-1918) o nome "pipa" foi atribuído a esse quadrilátero pelo matemático inglês James Joseph Sylvester (1814-1897).
Definição:
Uma pipa é um quadrilátero com uma simetria de reflexão em uma de suas diagonais, cujos seus quatro lados podem ser agrupados em dois pares de lados adjacentes congruentes.
Um quadrilátero é uma pipa se, e somente se, qualquer uma das condições forem verificadas:
- Os quatro lados pode ser divididos em dois pares de lados adjacentes congruentes;
- A diagonal que é seu eixo de simetria intercepta a outra diagonal em seu ponto médio em ângulo reto;
- A diagonal que é seu eixo de simetria divide-o em dois triângulos congruentes.
Propriedades:
Podemos observar algumas propriedades interessantes neste quadrilátero:
- Possui quatro ângulos e quatro vértices;
- As diagonais são perpendiculares entre si;
- Uma das diagonais é o eixo de simetria dividindo a pipa em dois triângulos congruentes;
- Os ângulos internos opostos ao eixo de simetria são congruentes;
- É um quadrilátero circunscritível, ou seja, possui uma circunferência inscrita tangente aos seus quatro lados.
O losango e o quadrado são casos especiais de pipa:
- As pipas equiláteras são losangos;
- As pipas equiangulares são quadrados.
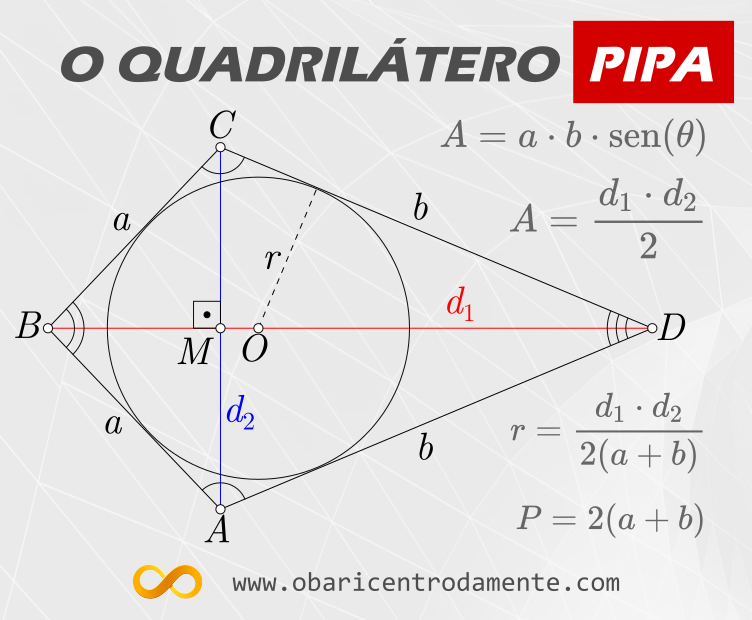
Elementos de uma pipa:
Onde:
- $a$ e $b$ são os lados da pipa;
- $A$, $B$, $C$ e $D$ são os vértices da pipa;
- $d_1$ e $d_2$ são as diagonais perpendiculares entre si;
- O eixo de simetria passa pela diagonal $d_1$;
- $M$ é o ponto médio da diagonal perpendicular ao eixo de simetria;
- $O$ é o centro da circunferência inscrita à pipa.
Área de uma pipa em função das diagonais:
A área de uma pipa é dada pelo semiproduto de suas diagonais:
$$A = \frac{d_1 \cdot d_2}{2}
$$
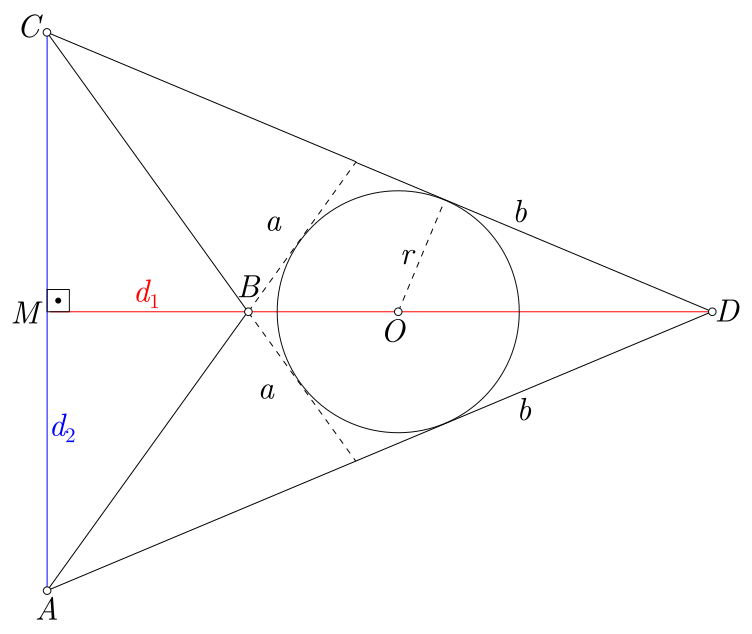
Para encontrarmos a fórmula para a área da pipa, consideremos a pipa $ABCD$:
Como a diagonal $d_1$ (que é seu eixo de simetria) divide a pipa em dois triângulo congruentes, temos que:
$$A = \triangle ABD + \triangle CBD \tag{1}
$$
A área de um triângulo é dada pelo semiproduto da base pela altura:
$$A_\triangle = \frac{b \cdot h}{2}
$$
Aplicando no triângulo $ABD$, temos:
$$A_{\triangle ABD} = \frac{\overline{BD} \cdot \overline{AM}}{2}\\
\ \\
A_{\triangle ABD} = \frac{\displaystyle d_1 \cdot \frac{d_2}{2}}{2}\\
$$
Encontrando:
$$A_{\triangle ABD} = \frac{d_1 \cdot d_2}{4} \tag{2}
$$
Aplicando no triângulo $CBD$, temos:
$$
A_{\triangle CBD} = \frac{\overline{BD} \cdot \overline{CM}}{2}\\
\ \\
A_{\triangle ABD} = \frac{\displaystyle d_1 \cdot \frac{d_2}{2}}{2}\\
$$
A_{\triangle CBD} = \frac{d_1 \cdot d_2}{4} \tag{3}
$$
A_{\triangle CBD} = \frac{\overline{BD} \cdot \overline{CM}}{2}\\
\ \\
A_{\triangle ABD} = \frac{\displaystyle d_1 \cdot \frac{d_2}{2}}{2}\\
$$
Encontrando:
$$A_{\triangle CBD} = \frac{d_1 \cdot d_2}{4} \tag{3}
$$
Substituindo $(2)$ e $(3)$ em $(1)$, obtemos:
$$A = \frac{d_1 \cdot d_2}{4} + \frac{d_1 \cdot d_2}{4}\\
\ \\
A = \frac{2(d_1 \cdot d_2)}{4}\\
\ \\
A = \frac{d_1 \cdot d_2}{2}
$$
Área de uma pipa em função dos lados e do ângulo formado por eles:
Se conhecermos os comprimentos dos lados desiguais da pipa e o ângulo formado por eles, podemos utilizar a trigonometria para calcular sua área. Podemos aplicar a seguinte fórmula para a área de um triângulo qualquer:
$$A_\triangle = \frac{a \cdot b \cdot \text{sen}(\theta)}{2}
$$
A demonstração desta fórmula pode ser acompanhada no artigo: 4 fórmulas par a área de um triângulo.
Aplicando no triângulo $ABD$ e utilizando a propriedade reflexiva da pipa, obtemos:
$$A = 2 \cdot \left( \frac{a \cdot b \cdot \text{sen}(\theta)}{2}\right)\\
\ \\
A = a \cdot b \cdot \text{sen}(\theta)
$$
Perímetro:
O perímetro da pipa é a soma dos comprimentos de seus quatro lados:
$$P = 2(a+b)
$$
Pipas côncavas:
Se o ângulo formado pelo par de lados iguais for maior do que 180°, a pipa se torna côncava. Embora sua forma não pareça mais com uma pipa, ainda satisfaz todas as propriedades de uma pipa.
Raio da circunferência inscrita:
O raio $r$ da circunferência inscrita a uma pipa é igual à razão entre o produto das diagonais e o perímetro:
$$r = \frac{d_1 \cdot d_2}{2(a+b)}
$$
Se a pipa convexa não é um losango, então existe uma circunferência externa à pipa que é tangente às extensões de seus quatro lados:
O raio $\rho$ da circunferência externa é dado por:
$$\rho = \frac{d_1 \cdot d_2}{2|a-b|}
$$
Dualidade:
Pipas e trapézios isósceles são duais entre si. A circunferência inscrita tangencia os lados da pipa em quatro pontos que são os vértices do trapézio isósceles. Do mesmo modo, uma circunferência inscrita em um trapézio isósceles fornece quatro pontos de tangência que são os vértices de uma pipa.
Referências:
- https://pt.wikipedia.org/wiki/Deltoide
- https://en.wikipedia.org/wiki/Kite_(geometry)
- https://www.cuemath.com/measurement/area-of-a-kite/
- A Cornucopia of Quadrilaterals - Claudi Alsina








Belíssimo conteúdo meu amigo! E como sempre, impecável em sua organização.
ResponderExcluirComo disse no Instagram, esse post me trouxe ótimas lembranças de um tempo lindo demais - a minha infância. Um tempo de brincar na rua sem preocupação com nada, sem violência, assalto, etc.
Obrigado pelo post, que além de Matemática, me trouxe essa nostalgia boa demais.
Um abração!
Obrigado, bonitão! Agradeço ua presença aqui.
ExcluirTem muito mais coisas sobre o quadrilátero pipa. Tive que focar em algumas propriedades apenas, porque, iria ficar muito longo. Talvez eu faça uma parte 2, quem sabe?
Quando criança, também brinquei muito de pipa. Como me divertia!
O bom da matemática é que ela está em todo o lugar!
Um abraço!