A Geometria Plana possui muitos teorema interessantes que podem ser demonstrados por métodos analíticos seguindo algumas etapas:
- Construir uma figura que represente o problema;
- Escolher um sistema cartesiano em posição conveniente;
- Fixar as coordenadas de pontos específicos da figura impondo hipóteses;
- Fazer a demonstração.
Teorema:
Em qualquer triângulo retângulo, a mediana relativa à hipotenusa é igual à metade da hipotenusa.
Antes de seguirmos, vamos relembrar alguns outros teorema necessários para esta demonstração.
Mediana:
A mediana é o segmento de reta que une um vértice de um triângulo ao ponto médio do lodo oposto a este vértice.
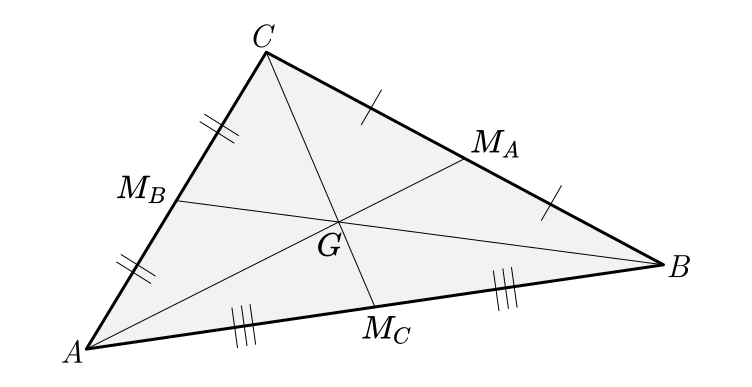
Na figura abaixo, vemos representadas as três medianas de um triângulo qualquer de vértices $ABC$:
A intersecção das três medianas é o baricentro do triângulo, representado pela letra $G$ e é considerado um dos pontos notáveis de um triângulo.
Ponto médio:
O ponto médio de um segmento de reta é aquele que o divide em outros dois segmentos congruentes entre si, isto é, de mesmo comprimento. As coordenadas do ponto médio são dadas por:
$$x_M = \frac{x_A+x_B}{2} \quad \text{e} \quad y_M=\frac{y_A+y_B}{2}
$$
onde $A$ e $B$ são as extremidades do segmento.
Se desejar, você pode ler o artigo com a demonstração: Como encontrar as coordenadas do ponto médio de um segmento de reta através da geometria analítica
Distância:
Distância é a medida do segmento de reta que une dois pontos. Se os pontos $A$ e $B$ podem ser representados em um plano cartesiano, então a distância entre eles é dada pela fórmula:
$$d_{AB} = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}
$$

Se desejar, você pode ler o artigo com a demonstração: Como calcular a distância entre dois pontos no plano
Demonstração:
Seja o triângulo retângulo de vértices $ABC$, retângulo em $A$. Podemos posicioná-lo convenientemente em um sistema cartesiano onde o vértice $A$ coincida com a origem:
Sendo assim, as coordenadas dos vértices desse triângulo são dadas por:
$$\begin{cases}
A (0,0)\\
\ \\
B(x,0)\\
\ \\
C(0,y)
\end{cases}
$$
Queremos demonstrar que o segmento $AM$ (mediana relativa à hipotenusa) é igual à metade do segmento $BC$ (hipotenusa), ou seja:
$$AM = \frac{BC}{2}
$$
Utilizando as fórmulas para o ponto médio de um segmento, obtemos:
$$
\begin{cases}
\displaystyle
x_M = \frac{x_B+x_C}{2} = \frac{x+0}{2} = \frac{x}{2}\\
\ \\
\displaystyle
y_M = \frac{y_B+y_C}{2} = \frac{0+y}{2} = \frac{y}{2}
\end{cases}
$$
d_{AM} = \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2}\\
\ \\
d_{AM} = \sqrt{\left( \frac{x}{2}-0 \right)^2 + \left(\frac{y}{2}-0\right)^2}\\
\ \\
d_{AM} = \sqrt{\frac{x^2}{4} + \frac{y^2}{4}}\\
\ \\
d_{AM} = \sqrt{\frac{x^2+y^2}{4}}\\
$$
d_{AM} = \frac{\sqrt{x^2+y^2}}{2} \tag{1}
$$
$$\begin{cases}
\displaystyle
x_M = \frac{x_B+x_C}{2} = \frac{x+0}{2} = \frac{x}{2}\\
\ \\
\displaystyle
y_M = \frac{y_B+y_C}{2} = \frac{0+y}{2} = \frac{y}{2}
\end{cases}
$$
Queremos encontrar o comprimento da mediana $AM$ em função das coordenadas $x$ e $y$. Para isso, utilizaremos a fórmula para a distância entre dois pontos:
$$d_{AM} = \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2}\\
\ \\
d_{AM} = \sqrt{\left( \frac{x}{2}-0 \right)^2 + \left(\frac{y}{2}-0\right)^2}\\
\ \\
d_{AM} = \sqrt{\frac{x^2}{4} + \frac{y^2}{4}}\\
\ \\
d_{AM} = \sqrt{\frac{x^2+y^2}{4}}\\
$$
Encontrando:
$$d_{AM} = \frac{\sqrt{x^2+y^2}}{2} \tag{1}
$$
Agora, fazemos o mesmo para o comprimento da hipotenusa $BC$:
d_{BC} = \sqrt{(x_C-x_B)^2 + (y_C-y_B)^2}\\
\ \\
d_{BC} = \sqrt{(0-x)^2 + (y-0)^2}
$$
Encontrando:
$$
d_{BC} = \sqrt{x^2+y^2} \tag{2}
$$
d_{BC} = \sqrt{x^2+y^2} \tag{2}
$$
Substituindo $(2)$ em $(1)$, obtemos:
$$d_{AM} = \frac{\sqrt{x^2+y^2}}{2}\\
\ \\
d_{AM} = \frac{d_{BC}}{2}
$$
Ou seja:
$$AM = \frac{BC}{2}
$$
Referências:
- Fundamentos de Matemática Elementar V7, Geometria Analítica, Gelson Iezzi






Postar um comentário