O Cálculo Diferencial estudas as taxas de mudanças de uma quantidade variável. A maioria dos fenômenos físicos ao nosso redor envolve quantidades que se alteram com o passar do tempo, como por exemplo a velocidade de um automóvel em movimento, as leituras de temperatura em um ambiente, a corrente elétrica circulando em um circuito. Hoje chamamos essas quantidades de variáveis. Newton usava o termo fluente.
O Cálculo Diferencial está relacionado à descoberta da taxa de mudança de uma variável. Usando a expressão de Newton, a fluxão de um determinado fluente. A escolha dessas palavras revelam como a mente de Newton pensava o problema. Sua visão de mundo era dinâmica, onde tudo se encontra em um estado contínuo de movimento causado por foças conhecidas.
Claro que esta visão não era exclusiva de Newton. Tentativas de explicar como certas forças atuavam no movimento recuam até a antiguidade, chegando ao seu clímax quando Galilei Galilei (1564-1642) estabeleceu as fundações da mecânica no início do século XVII. Mas foi Newton quem unificou o conjunto dos fatos observacionais conhecidos em uma grande teoria, a Lei da Gravitação, que ele enunciou em sua obra Philosophiæ Naturalis Principia Mathematica publicada em 1687. Sua invenção do Cálculo, embora diretamente relacionada com seu trabalho na Física, foi sem dúvida influenciada por sua visão dinâmica do Universo.
O ponto de partida de Newton foi considerar duas variáveis que se relacionavam em uma equação. Hoje chamamos esse tipo de de relacionamento de função e usamos a notação $y=f(x)$ para indicar que $y$ é uma função de $x$.
Newton imaginou o gráfico de uma função como uma curva gerada por um ponto móvel $P(x,y)$. à medida que $P$ traça a curva, ambas as coordenadas $x$ e $y$ variam continuamente com o tempo. Ele imaginava o próprio tempo como fluindo a uma taxa uniforme, daí a palavra fluente.
O próximo passo foi encontrar as taxas de mudança de $x$ e $y$ em relação ao tempo, isto é, suas fluxões. Ele conseguiu isso considerando a diferença, ou a mudança, nos valores de $x$ e $y$ entre dois pontos adjacentes, dividindo essa diferença pelo intervalo de tempo transcorrido próximo de zero, ou melhor, tão pequeno a ponto de ser desprezível.
Vamos tomar como exemplo a relação $y=x^2$, que gera uma parábola quando representada por um gráfico no plano $xy$. Vamos considerar um pequeno espaço de tempo, denotado por $\varepsilon$. Durante esse intervalo de tempo a coordenada $x$ muda na quantidade $\dot{x} \varepsilon$, onde $\dot{x}$ é a notação de Newton para a taxa de mudança, ou fluxão, de $x$, que ficou conhecida como notação do ponto. De modo semelhante, a mudança em $y$ é $\dot{y} \varepsilon$.
Substituindo $x$ por $x+\dot{x}\varepsilon$ e $y$ por $y+\dot{y} \varepsilon$ na equação $y=x^2$, teremos:
$$y + \dot{y} \varepsilon = (x + \dot{x}\varepsilon)^2\\
\ \\
y + \dot{y} \varepsilon = x^2 + 2x\ \dot{x}\varepsilon + \left(\dot{x}\varepsilon \right)^2
$$
Mas como o $y$ do membro da esquerda pode ser cancelado com o $x^2$ da direita (pois $y=x^2$), obtemos:
$$\dot{y}\varepsilon = 2x \ \dot{x} \varepsilon + \left(\dot{x}\varepsilon \right)^2
$$
Dividindo ambos os membro por $\varepsilon$, teremos:
$$
\dot{y} = 2x\ \dot{x} + \dot{x}^2 \varepsilon
$$
Como o intervalo de tempo é desprezível, fazemos $\varepsilon = 0$, o que nos deixa com:
$$\dot{y} = 2x \ \dot{x}
$$
Esta relação entre as fluxões dos dois fluentes $x$ e $y$, ou, em linguagem moderna, entre as taxas de mudança das variáveis $x$ e $y$, e cada uma considerada como uma função do tempo. Se dividirmos a fluxão de $y$ pela de $x$ teremos a taxa de variação de $y$ em relação a $x$:
$$\frac{\dot{y}}{\dot{x}}
$$
onde o significado geométrico desta razão mede a inclinação da reta tangente para uma curva no ponto $P(x,y)$, onde inclinação representa a proporção em que a reta se eleva naquele ponto.
Deste modo, para a parábola $y=x^2$, encontramos a relação entre as duas fluxões $\dot{y}=2x\ \dot{x}$, de modo que:
$$\frac{\dot{y}}{\dot{x}} = 2x
$$
Isto significa que para cada ponto $P(x,y)$ na parábola, a reta tangente tem uma inclinação igual a duas vezes o valor da coordenada $x$ naquele ponto. Se $x=3$, a inclinação é $6$; se $x=-3$, a inclinação é $-6$. Uma inclinação negativa significa que a curva está descendo à medida que nos movemos da esquerda para a direita. Se $x=0$, a inclinação é $0$ e significa que a parábola tem uma reta tangente horizontal em $x=0$.
Newton deu vários exemplos de como funciona seu Método das Fluxões. O método é totalmente generalizado, podendo ser aplicado a quaisquer fluentes que se relacionem entre si atrvés de uma equação.
Embora Newton pensasse me $x$ e $y$ variando com o tempo, ele terminou com uma intepretação puramente geométrica das fluxões, a qual não depende do tempo. Ele precisou da noção de tempo apenas como uma ajuda mental para cristalizar suas ideias.
Newton aplicou seu método em um número grande de curvas, encontrando suas inclinações, seus pontos mais altos e mais baixos (máximos e mínimos) e seus pontos de inflexão. Devido a essa associação com a tangente, o processo de encontrar a fluxão de um determinado fluente era conhecido, na época, como problema da tangente. Hoje, chamamos esse processo de diferenciação e a fluxão de uma função chamamos de derivada.
A notação do ponto de Newton não sobreviveu, muito embora, ocasionalmente possa ser encontrada em alguns livros. Atualmente usamos a notação diferencial de Leibniz, que é muito mais eficiente:
$$\frac{dy}{dx}
$$
A importância da invenção de Newton é que ele forneceu um procedimento geral, um algoritmo, para encontrar a taxa de mudança de praticamente qualquer função. A maioria das regras de diferenciação, que agora são parte dos cursos de Cálculo, foram descobertas por ele.
Por exemplo, para funções do tipo $y=x^n$, temos:
$$\dot{y} = n\ x^{n-1}\ \dot{x}
$$
onde $n$ representa qualquer valor, positivo ou negativo, inteiro ou fracionário e até mesmo irracional.
Seus predecessores abriram o caminho, mas foi Newton quem transformou suas ideias em uma poderosa ferramenta que logo seria aplicada com enorme sucesso em todos os ramos das ciências.
Vamos ver outro exemplo um pouco mais complicado dado por Newton. Consideremos a cúbica $y=x^3-2x^2+x-1$. Tomemos um espaço muito pequeno de tempo $\varepsilon$, de modo que a coordenada $x$ se desloca uma quantidade $\dot{x}\varepsilon$ e a corrdenada $y$ uma quantidade $\dot{y}\varepsilon$. Em seguida, substituímos $x$ por $x+\dot{x}\varepsilon$ e $y$ por $y+\dot{y}\varepsilon$:
$$y+\dot{y}\varepsilon = \color{blue}{(x+\dot{x}\varepsilon)^3} - \color{red}{2(x+\dot{x}\varepsilon)^2} + \color{green}{(x+\dot{x}\varepsilon)}-\color{orange}{1}\\
\ \\
y+\dot{y}\varepsilon = \color{blue}{x^3+3x^2\dot{x}\varepsilon+3x(\dot{x}\varepsilon)^2+(\dot{x}\varepsilon)^3}\\
\ \\
-\color{red}{2\big(x^2+2x\dot{x}\varepsilon+(\dot{x}\varepsilon)^2\big)}+ \color{green}{x+\dot{x}\varepsilon} - \color{orange}{1}\\
\ \\
y+\dot{y}\varepsilon = \color{blue}{x^3+3x^2\dot{x}\varepsilon+3x\dot{x}^2\varepsilon^2+\dot{x}^3\varepsilon^3}\\
\ \\
-\color{red}{2x^2-4x\dot{x}\varepsilon-2\dot{x}^2\varepsilon^2}+ \color{green}{x+\dot{x}\varepsilon} - \color{orange}{1}
$$
Como $y=x^3-2x^2+x-1$, podemos efetuar o cancelamento:
$$\dot{y}\varepsilon = \color{blue}{3x^2\dot{x}\varepsilon+3x\dot{x}^2\varepsilon^2+\dot{x}^3\varepsilon^3}\\
\ \\
-\color{red}{4x\dot{x}\varepsilon-2\dot{x}^2\varepsilon^2}+ \color{green}{\dot{x}\varepsilon}
$$
Dividindo a equação por $\varepsilon$:
$$\dot{y} = \color{blue}{3x^2\dot{x}+3x\dot{x}^2\varepsilon+\dot{x}^3\varepsilon^2}\\
\ \\
-\color{red}{4x\dot{x}-2\dot{x}^2\varepsilon}+ \color{green}{\dot{x}}
$$
Como o espaço de tempo é desprezível, fazemos $\varepsilon=0$:
$$\dot{y} = 3x^2\dot{x} - 4x\dot{x} + \dot{x}\\
\ \\
\dot{y} = (3x^2-4x+1)\dot{x}
$$
Encontramos a relação entre as fluxões dos dois fluentes $x$ e $y$. Se dividirmos a fluxão de $x$ pela de $y$, teremos a taxa e variação de $y$ em relação a $x$:
$$\frac{\dot{y}}{\dot{x}} = 3x^2-4x+1
$$
Que é o mesmo resultado que obtemos se aplicarmos o método moderno para encontrar a derivada de um polinômio, o que não surpreende, mas conforta.
Newton considerou o inverso do problema da tangente: dada uma fluxão, qual seria seu fluente?
De um modo geral, o problema da integração é mais difícil do que da diferenciação, assim como a divisão é uma operação mais difícil do que a multiplicação, assim como a extração da raiz quadrada é mais difícil do que elevar uma quantidade ao quadrado.
Casos simples podem ser obtidos por "palpites", como no exemplo da parábola: dada a fluxão $\dot{y}=2x\ \dot{x}$, encontrar o fluente $y$.
Uma resposta óbvia é $y=x^2$. Mas $y=x^2+1$ também é verdadeira, assim como $y=x^2+2$, ou $y=x^2+3$, ou, de fato, $y=x^2+C$, onde $C$ é qualquer constante. A razão para isso é que os gráficos de todas essas funções são obtidas a partir do gráfico de $y=x^2$, deslocando-se verticalmente pelo eixo dos $y$, resultando que todos os gráfico possuem tangentes com mesma inclinação em um mesmo ponto $x$.
A inclinação das retas tangentes permanecem invariáveis quando a curva é deslocada para cima ou para baixo.
Tendo demonstrado que a fluxão de $y=x^n$ é $\dot{y}=n\ x^{n-1}\ \dot{x}$, Newton inverteu a fórmula, de modo que agora dizia: Se a fluxão for $\dot{y}=x^n\ \dot{x}$, então o fluente (desconsiderando a constante a ele somada) será:
$$y = \frac{x^{n+1}}{n+1}
$$
Podemos conferir este resultado através da diferenciação, obtendo:
$$\dot{y} = x^n\ \dot{x}
$$
A fórmula de Newton para o problema inverso também se aplica a valores fracionários para $n$, assim como para inteiros.
Um dos exemplos de Newton foi, se $\dot{y} = x^{1/2}\ \dot{x}$, então $\displaystyle y=\frac{2}{3}x^{3/2}$. Mas a fórmula falha se $n=-1$, pois assim, o denominador se torna $0$. Este é o caso onde a fluxão é proporcional a $1/x$, o mesmo caso que desafiara Fermat em suas tentativas para obter a quadratura da hipérbole. Newton sabia que o resultado envolvia logaritmos, chamando de logaritmos hiperbólicos para distingui-los dos logaritmos "comuns" de Briggs.
Hoje, chamamos de integração indefinida ou antididerenciação ao processo de encontrar o fluente de uma determinada fluxão, e o resultado de integrar uma dada função é a sua integral indefinida ou antiderivada.
Newton fez mais do que apenas fornecer regras para a diferenciação e a integração.
Fermat, em suas pesquisas sobre encontrar áreas sob curvas, descobriu que a área sob a curva $y=x^n$, de $x=0$ até algum $x>0$, é dada pela expressão:
$$\frac{x^{n+1}}{n+1}
$$
que é a mesma expressão que surge da antidiferenciação de $y=x^n$.
Newton reconheceu que esta conexão entre a área e a antidiferenciação não era coincidência. Em outras palavras, ele percebeu que os dois problemas fundamentais do Cálculo eram problemas inversos, ou seja, o problema da tangente e o problema da área. Este é o ponto principal do Cálculo Diferencial e Integral.
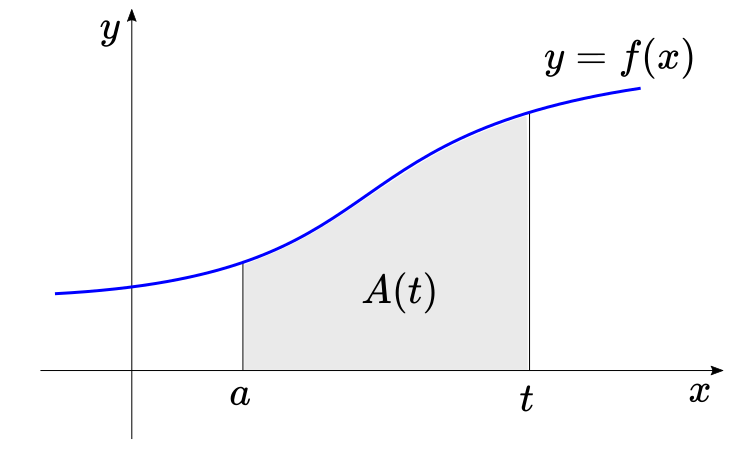
Dada uma função $y=f(x)$, podemos definir uma nova função $A(t)$, que representa a área sob o gráfico de $f(x)$, de um valor fixo $x=a$ a algum valor variável $x=t$. Vamos chamar essa nova função de função de área da função original.
Se o valor de $x=t$ varia para direita ou para esquerda, a área sob o gráfico também varia, justamente porque $A(t)$ é uma função de $t$.
Newton percebeu que a taxa de mudança da função de área $A(t)$, em um ponto $x=t$ é igual ao valor da função original nesse ponto. Em outras palavras, a derivada de $A(t)$ e igual a $f(t)$, o que, por sua vez, significa que $A(t)$ é a antiderivada de $f(t)$.
Para encontrarmos a área sob uma certa curva $f(x)$, deveremos encontrar a antiderivada de $f(x)$, substituindo a variável $t$ por $x$. É nesse sentido que os dois processos – encontrar a área sob a curva e encontrar a derivada – são opostos um do outro. Hoje me dia, esta relação inversa é conhecida como Teorema Fundamental do Cálculo.
Newton não faz uma demonstração formal do Teorema Fundamental, mas compreendeu plenamente a sua essência.
A descoberta de Newton fundiu dois ramos do Cálculo em um único campo unificado, pois até então, eram considerados assuntos distintos.
Como exemplo, vamos encontrar a área sob a parábola $y=x^2$, de $x=1$ a $x=2$.
Primeiramente, devemos encontrar uma antiderivada de $y=x^2$. Já sabemos que as antiderivadas de $x^2$ são dadas por $\displaystyle y=\frac{x^3}{3}+C$, de modo que a função de área $\displaystyle A(x)=\frac{x^3}{3}+C$.
Para determinarmos o valor de $C$, notamos que, em $x=1$ a área deve ser igual a $0$, porque este é o ponto inicial do intervalo. Assim:
$$A(1) = 0 = \frac{1^3}{3}+C = \frac{1}{3}+C
$$
De modo que:
$$C = -\frac{1}{3}
$$
Substituindo esse valor de volta na equação para $A(x)$, teremos:
$$A(x) = \frac{x^3}{3}-\frac{1}{3}
$$
Finalmente, substituindo $x=2$ nesta equação, encontraremos:
$$A(2) = \frac{2^3}{3}-\frac{1}{3}\\
\ \\
A(2) = \frac{8}{3}-\frac{1}{3}\\
\ \\
A(2) = \frac{7}{3}
$$
Assim, a área desejada vale $7/3$ unidades de área.
Quando consideramos quanto trabalho seria necessário para chegar ao mesmo resultado pelo método da exaustão, ou mesmo pelo método dos indivisíveis, passamos a apreciar enormemente a vantagem do Cálculo Integral.
Referências:
- e, A História de um Número - Eli Maor





Nice post thank you Christopher
ResponderExcluir