Como encontrar as coordenadas do ponto médio de um segmento de reta através da geometria analítica

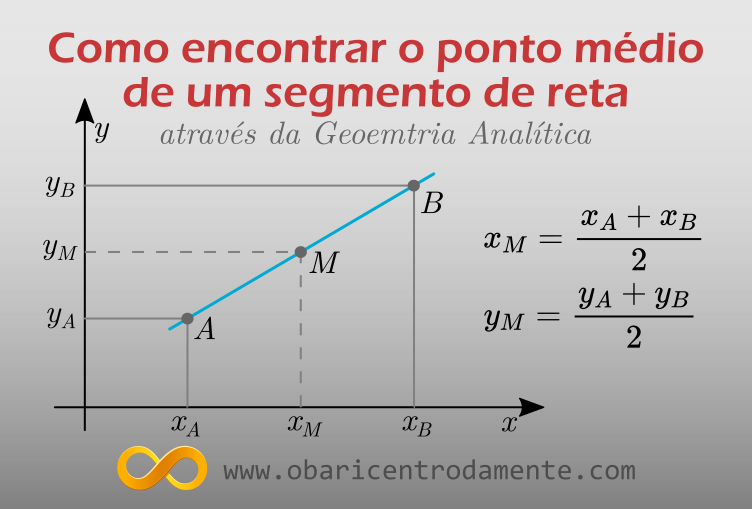
O ponto médio de um segmento de reta é aquele que o divide em dois outros segmentos congruentes entre si, isto é, de mesmo comprimento.

Dado um segmento de reta $\overline{AB}$ no plano cartesiano, as coordenadas dos pontos $A$, $B$ e $M$ são:

$$
A(x_A,y_A) \quad , \quad B(x_B,y_B) \quad , \quad M(x_M,y_M)
$$

Se $M$ é o ponto médio do segmento $\overline{AB}$, então temos que:

$$
\overline{AM} = \overline{MB}
$$

E a razão $r$ entre os segmentos é dada por:

$$
r = \frac{\overline{AM}}{\overline{MB}} = 1
$$

Pois a razão entre duas quantidades iguais é a unidade.

Para encontrarmos a distância entre dois pontos, fazemos uma subtração:

$$
d_{AB} = B-A
$$

Assim, para as coordenadas $x$, fazemos:

$$
\overline{AM}=\overline{MB}\\
\ \\

x_M - x_A = x_B-x_M\\
\ \\
x_M+x_M = x_A+x_B\\
\ \\
2x_M = x_A+x_B\\
\ \\
\boxed{x_M = \frac{x_A+x_B}{2}}
$$

E para as coordenadas $y$, fazemos:

$$
\overline{AM}=\overline{MB}\\
\ \\
y_M - y_A = y_B-y_M\\
\ \\
y_M+y_M = y_A+y_B\\
\ \\
2y_M = y_A+y_B\\
\ \\
\boxed{y_M = \frac{y_A+y_B}{2}}
$$

Exemplo 1:

Dado o segmento $\overline{AB}$, sendo $A(6,3)$ e $B(-2,-1)$, encontrar as coordenadas do ponto médio.

$$
x_M = \frac{x_A+x_B}{2}=\frac{6-2}{2}=\frac{4}{2}=2\\

\ \\
y_M = \frac{y_A+y_B}{2}=\frac{3-1}{2}=\frac{2}{2}=1
$$

Assim, as coordenadas do ponto médio do segmento $\overline{AB}$ são:

$$
M(2,1)
$$

Exemplo 2:

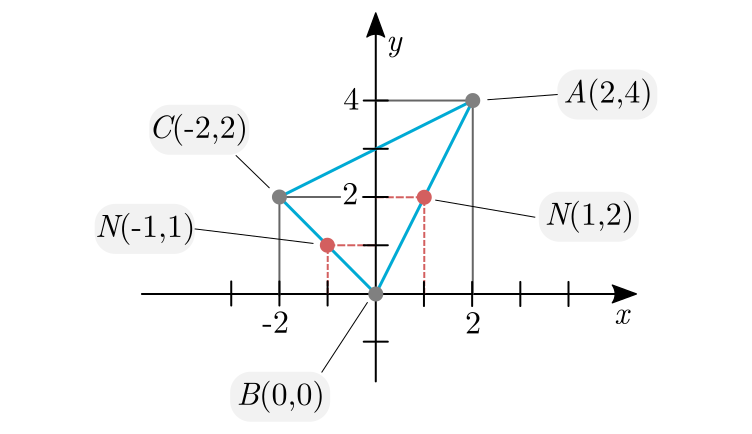
Dado um triângulo $ABC$, sendo $M$ p ponto médio de $\overline{AB}$ e $N$ o ponto médio de $\overline{BC}$, calcular o perímetro do triângulo sabendo que $A(2,4)$, $M(1,2)$ e $N(-1,1)$.

Se $M$ é o ponto médio de $\overline{AB}$, então:

$$
\begin{matrix}
x_M=\cfrac{x_A+x_B}{2} & && y_M = \cfrac{y_A+y_B}{2}\\
1=\cfrac{2+x_B}{2} && & 2 = \cfrac{4+y_B}{2}\\
3 = 2 + x_B && & 4 = 4 + y_B\\
x_B = 0 & && y_B=0
\end{matrix}
$$

Portanto, $B(0,0)$.

Se $N$ é o ponto médio do semento $\overline{BC}$, então:

$$
\begin{matrix}
x_N=\cfrac{x_B+x_C}{2} && & y_N = \cfrac{y_B+y_C}{2}\\
-1=\cfrac{0+x_C}{2} && & 1 = \cfrac{0+y_C}{2}\\
x_C = -2 & && y_C=2
\end{matrix}
$$

Portanto, $C(-2,2)$.

O perímetro $P$ é dado pela soma dos três lados do triângulo. Utilizamos a fórmula para calcular a distância entre dois pontos no plano:

O lado $AB$ mede:

$$
d_{AB} = \sqrt{(0-(-2))^2+(0-4)^2}\\
\ \\
d_{AB}=\sqrt{4+16}\\
\ \\
d_{AB}=\sqrt{20}
$$

O lado $BC$ mede:

$$
d_{BC} = \sqrt{(-2-0)^2 + (2-0)^2}\\
\ \\
d_{BC}=\sqrt{4+4}\\
\ \\
d_{BC}=\sqrt{8}
$$

O lado $CA$ mede:

$$
d_{CA} = \sqrt{(2-(-2))^2+(4-2)^2}\\
\ \\
d_{CA}=\sqrt{16+4}\\
\ \\
d_{CA}=\sqrt{20}
$$

O perímetro $P$ é dado pela somas dos lados:

$$
P = d_{AB} + d_{BC} + d_{CA}\\
\ \\
P = \sqrt{20} + \sqrt{8} + \sqrt{20}\\
\ \\
P = 2\sqrt{5} + 2\sqrt{2} + 2\sqrt{5}\\
\ \\
P = 4\sqrt{5}+2\sqrt{2}
$$

Assim, o perímetro do triângulo mede $4\sqrt{5}+2\sqrt{2}$ unidades de comprimento.

Links para este artigo:

• https://bit.ly/ponto-medio-segmento
  
• https://www.obaricentrodamente.com/2022/07/como-encontrar-as-coordenadas-do-ponto-medio-de-um-segmento-de-reta-atraves-da-geometria-analitica.html

Veja mais:

• Como calcular distância través da geometria analítica
• Distância de um ponto a uma reta
  
• Distância entre dois pontos no plano
  
• Teorema da base média de um triângulo
  
• Como treinei meu cérebro para ser fluente em matemática no blog do Professor Edigley Alexandre