O matemático grego Hipócrates de Chio (cerca de470 a.C - 410 a.C.), parece ter sido o primeiro a calcular a área exata de uma figura delimitada por curvas. Não confundir com o médico Hipócrates de Cos.
Hipócrates nasceu em Quio (Chios), uma ilha do arquipélago de Dodecaneso na Grécia. Era originalmente um mercador, cujos bens foram roubados por piratas. Ele então seguiu para Atenas onde viveu por muitos anos, estudou Matemática e compilou um livro sobre os elementos de matemática que influenciou fortemente Euclides (cerca de 325 a.C. - 265 a.C.) em seus Elementos um século mais tarde.
As informações sobre sua vida e obra têm como fonte principal relatos indiretos de Aristóteles (384 a.C. - 322 .C.) que fez um relato sobre a infelicidade de Hipócrates de ter sido alvo de pirataria: "Gente brilhante me determinado campo pode ser bastante tolo em muitas outras coisas. Assim, Hipócrates, embora hábil em Geometria, era estúpido e fraco que deixou um coletor de impostos de Bizâncio fraudá-lo numa fortuna". Isso foi escrito por um homem que afirmou que corpos mais pesados caem ao chão mais rapidamente e que os homens têm mais dentes que as mulheres.
Para compreendermos o que Hipócrates fez, descrevemos um círculo de raio $r = OA$ centrado em $O$. Marcamos os pontos $A$, $B$, $C$ e $D$ nas extremidades dos diâmetros horizontal e vertical. Em seguida, centrado em $C$ e raio $\overline{CA}$, descrevemos um arco $AEB$. A figura gerada lembra a forma de uma lua crescente (ou minguante) limitada pelos arcos $ADB$ e $AEB$.
Essa figura foi chamada de Lúnula de Hipócrates em homenagem àquele que fez a notável descoberta de que sua área é igual à área do quadrado de lado igual ao raio $OA$ do círculo. O sucesso de Hipócrates na quadratura de certas lúnulas, provavelmente foi de suas investigações sobre a quadratura do círculo. Assim, Hipócrates "quadrou" a lúnula, embora seja impossível quadrar o círculo.
Esse teorema (muito surpreendente, ainda mais para a época em que foi proposto) parece ser o primeiro cálculo preciso de uma área de uma região limitada por curvas. A demonstração é simples, mas engenhosa e depende de um conhecimento prévio de outros conceitos geométricos:
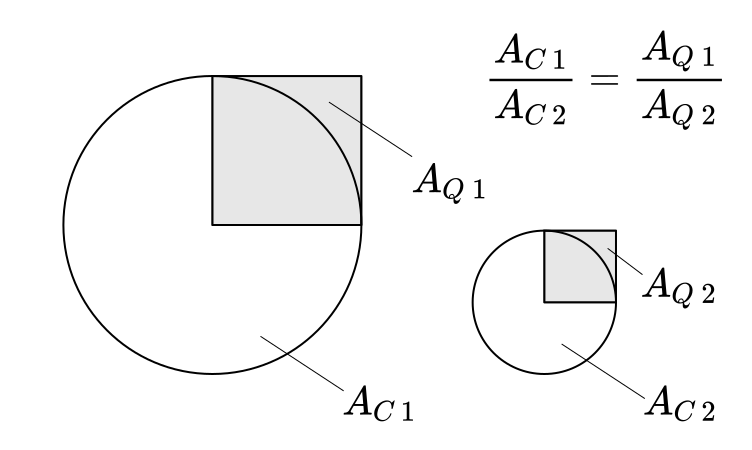
a) As áreas de dois círculos estão entre si assim como os quadrados de seus raios:
b) Os setores de dois círculos com ângulos centrais iguais estão entre si assim como os quadrados dos raios:
c) Os segmentos de dois círculos com ângulos centrais iguais estão entre si assim como os quadrados dos raios:
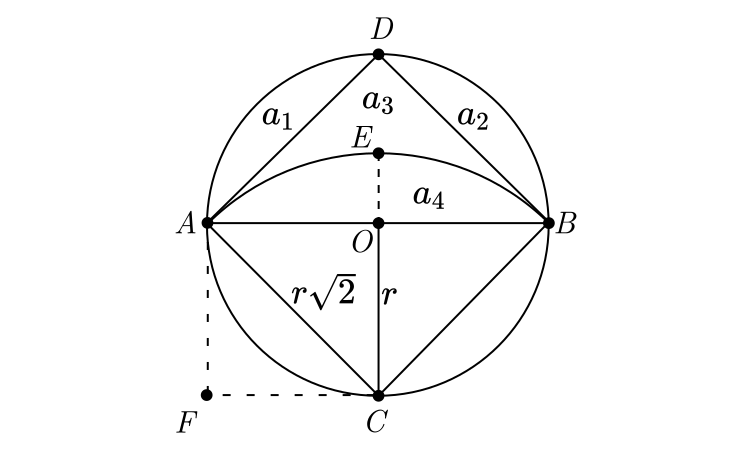
Para a demonstração, vamos redesenhar o problema considerando as lúnulas:
As cordas $\overline{AD}$ e $\overline{BD}$ são tangentes ao arco $AEB$, dividindo a lúnula em três regiões com áreas iguais a $a_1$, $a_2$ e $a_3$. Denotando o raio do círculo centrado em $O$ por $r$, podemos utilizar o Teorema de Pitágoras aplicado ao triângulo $AOC$, encontrando como $r\sqrt{2}$ a hipotenusa $\overline{AC}$.
As áreas $a_1$ e $a_2$ são segmentos do círculo de raio $r$ e $a_4$ é um segmento do círculo de raio $r\sqrt{2}$, sendo todos com ângulos centrais retos.
Utilizando a proposição dada em $c)$, temos que:
$$\frac{a_1}{a_4} = \frac{r^2}{\Big(r\sqrt{2}\Big)^2} = \frac{1}{2}
$$
Isso mostra que:
$$a_1 = \frac{1}{2} a_4 \quad \text{e} \quad a_2 - \frac{1}{2} a_4
$$
E que:
$$a_1+a_2=a_4
$$
A área do triângulo $ABD$ é a metade do quadrado $ABCD$ de lado $r\sqrt{2}$:
$$A_{ABD} = \frac{\Big(r\sqrt{2}\Big)^2}{2} = \frac{2r^2}{2} = r^2
$$
A área $a_3$ é dada por:
$$a_3 = A_{ABD} - a_4 = r^2 -(a_1+a_2)
$$
E a área da lúnula é igual a:
$$A_L = a_1+a_2+a_3\\
\ \\
A_L = a_1+a_2+\Big( r^2-(a_1+a_2)\Big)\\
\ \\
A_L = r^2
$$
Como pretendíamos demonstrar.
Hipócrates foi contemporâneo de Péricles (cerca de 495 a.C. - 429 a.C.), um grande estadista, líder político e cultural de Atenas na Idade de Ouro, mas nada do legado de Péricles tem a qualidade duradoura dessas bela descoberta geométrica. Até mesmo o Parthenon, cujo projeto e construção supervisionou, está se desintegrando.
O raciocínio de Hipócrates é modelo de prova matemática intocada pelo tempo. Em poucos passos elegantes converte algo fácil de entender mas difícil de acreditar, em algo impossível de duvidar.
Referências:
- Cálculo com Geometria Analítica V1 e V2 - Simmons
- Introdução à História da Matemática - Howard Eves







SENSACIONAL!!
ResponderExcluirObrigado, amigo, por dedicar seu tempo na leitura. Um abraço!
ExcluirAdorei! Brilhante! :)
ResponderExcluir